在计算机算法求解问题当中,经常用时间复杂度和空间复杂度来表示一个算法的运行效率。空间复杂度表示一个算法在计算过程当中要占用的内存空间大小;时间复杂度则表示这个算法运行得到想要的解所需的计算工作量,并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快,即探讨的是当输入值接近无穷时,算法所需工作量的变化快慢程度。也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。
Gary Chan
你永远流淌在我的记忆里?River flows in you
No results found
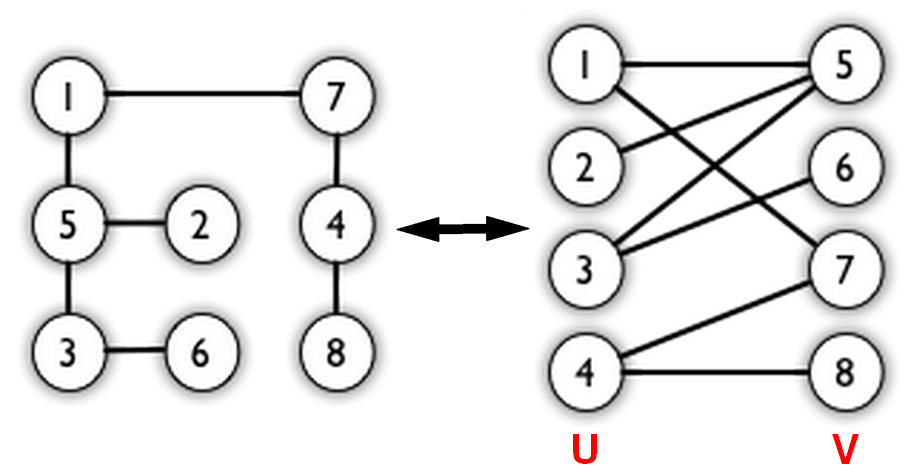
算法设计与分析[0016] 二分图匹配问题
算法设计与分析[0015] Union Find Set(并查集)
算法设计与分析[0014] Dynamic Programming(V) 一道习题
- Consider the following game. A “dealer” produces a sequence $s_1, …, s_n$ of “cards”, face up, where each card $s_i$ has a value $v_i$. Then two players take turns picking a card from the sequence, but can only pick the first or the last card of the (remaining) sequence. The goal is to collect cards of largest total value. (For example, you can think of the cards as bills of different denominations.) Assume n is even.
算法设计与分析[0013] 网络流:最大流(Max Flow)问题
算法设计与分析[0012] Dynamic Programming(IV)(Longest Palindromic Subsequence)
所谓 回文(palindrome),指的是正读和反读都是一样的。而 字符子串 和 字符子序列 的区别,在前面 算法设计与分析[0011] Dynamic Programming(III)(Longest Common Subsequence) 中也有提到过,字符字串指的是字符串中连续的n个字符,而字符子序列指的是字符串中不一定连续但先后顺序与原字符串一致的n个字符。
算法设计与分析[0011] Dynamic Programming(III)(Longest Common Subsequence)
子序列和子字符串的不同之处在于,子序列不需要是原序列上连续的字符。对于 Longest Common Substring 以及 Longest Common Subsequence 这类题目,大多数需要用到 DP 的思想,其中,状态转移是关键。
算法设计与分析[0010] Longest Increasing Subsequence(最长递增子序列)
300. Longest Increasing Subsequence
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example, Given [10, 9, 2, 5, 3, 7, 101, 18], The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
- 给出一个序列 $a_1, a_2, …, a_n$,求它的一个子序列(设为 $s_1, s_2, …, s_n$ ),使得这个子序列满足这样的性质:$ s_1 < s_2 < s_3 <…< s_n $ 并且这个子序列的长度最长,输出这个最长的长度。实际上,诸如最长下降子序列,最长不上升子序列等问题都可以看成同一个问题,仔细思考就会发现,这其实只是 $<$ 符号定义上的问题,并不影响问题的实质。