嵌入式系统实验课大概涉及的内容有以下几个部分:
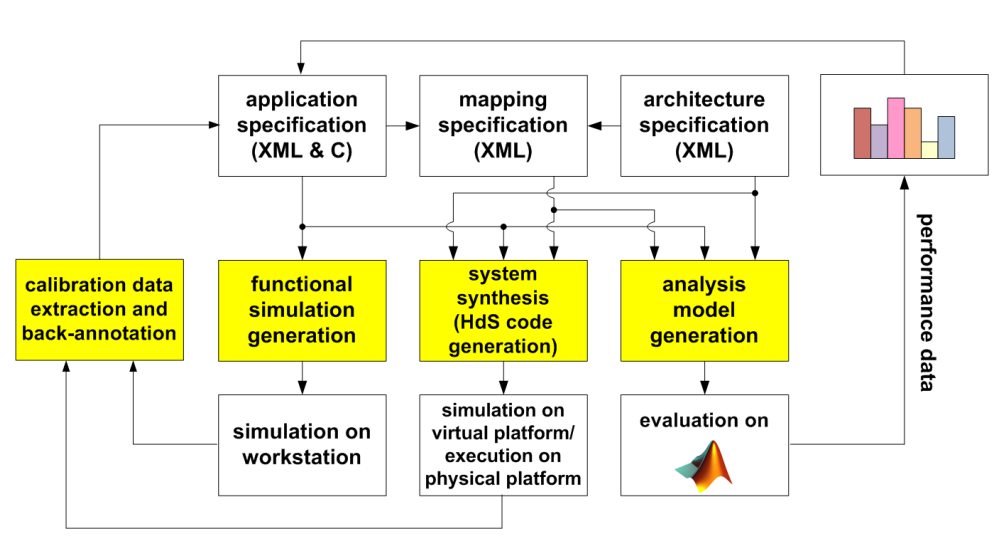
主体就涵盖了三条纵线一条横线,functional simulation,Hds simulation,analysis model 是三纵,如何通过三纵得到的数据迭代获取 application 和 architecture 的最佳 mapping 为一横。
你永远流淌在我的记忆里?River flows in you
No results found
嵌入式系统实验课大概涉及的内容有以下几个部分:

本文主要介绍 BFS 的 C++ 和 C 语言实现,并借助 LeetCode 上的一道题,说说基本的 BFS 在问题求解中的应用。
广度优先搜索算法(Breadth First Search),又叫宽度优先搜索,或横向优先搜索。是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
一些计算机程序设计中常用的线性数据结构:Array、ArrayList、LinkedList、List、Stack、Queue、Hashtable 和Dictionary。为了更高效的进行数据的查找和访问,例如避免普通数据查找的 $O(N)$ 线性时间复杂度,常用树这种数据结构保存数据。
树(Tree)是由多个节点(Node)的集合组成,每个节点又有多个与其关联的子节点(Child Node);子节点就是直接处于节点之下的节点,而父节点(Parent Node)则位于节点直接关联的上方;树的根(Root)指的是一个没有父节点的单独的节点。所有的树都呈现了一些共有的性质:①只有一个根节点;②除了根节点,所有节点都有且只有一个父节点;③无环。将任意一个节点作为起始节点,都不存在任何回到该起始节点的路径(正是前两个性质保证了无环的成立)。
更高效同时也相对更加复杂的树型数据结构包括 BST(二叉查找树)、R-B Tree(红黑树)、AVL Tree(平衡二叉树:父节点的左子树和右子树的高度之差不能大于1)、Treap(树堆:满足①二叉查找树的性质;满足②堆的性质)、Splay Tree(伸展树:在一次搜索后,会对树进行一些特殊的操作,这些操作的理念与AVL树有些类似,即通过旋转,来改变树节点的分布,并减小树的深度;伸展树并没有AVL树的平衡要求,任意节点的左右子树可以相差任意深度)、B-Tree(B树:多叉平衡查找树,B$^{+}$-Tree(B+树)是B树的变体)等。
本文主要介绍基础的 BST(二叉查找树)以及提升搜索效率的更高级的数据结构:R-B Tree(红黑树)。
References:
MOxFIVE 自定义的 Yelee 这个主题真的很好用,迁移之后我的几个体会是:
a). 动态效果很酷炫,整个界面给人的感觉就很满意
b). 添加多说评论栏是如此的简单
c). 自带的站点、页面访问量统计,很不错
d). 整个源码的框架似乎更合理了,你可以自己浏览一下源码,感同身受吧?
下面是本人将自己的博客主题迁移到 Yelee 的过程以及其中做的一些自定义适配。
在计算机算法求解问题当中,经常用时间复杂度和空间复杂度来表示一个算法的运行效率。空间复杂度表示一个算法在计算过程当中要占用的内存空间大小;时间复杂度则表示这个算法运行得到想要的解所需的计算工作量,并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快,即探讨的是当输入值接近无穷时,算法所需工作量的变化快慢程度。也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。
本文将介绍带权图的最小生成树(Minimum Spanning Tree)算法:给定一个无向图 G,并且它的每条边均有权值,则 MST 是一个包括 G 的所有顶点及边的子集的图,这个子集保证图是连通的,并且子集中所有边的权值之和为所有子集中最小的。
本文中介绍两种求解图的最小生成树的算法:Prim 算法和 Kruskal 算法,这两种算法都是贪心算法。一般而言,贪心策略不一定能保证找到全局最优解,但是对最小生成树问题来说,贪心策略能获得具有最小权值的生成树。
所谓 回文(palindrome),指的是正读和反读都是一样的。而 字符子串 和 字符子序列 的区别,在前面 算法设计与分析[0011] Dynamic Programming(III)(Longest Common Subsequence) 中也有提到过,字符字串指的是字符串中连续的n个字符,而字符子序列指的是字符串中不一定连续但先后顺序与原字符串一致的n个字符。