2017-10-24

嵌入式系统导论[03] Model of Computation

　承接前期DOL Functional Simulation 和 MPARM Simulation的实验内容，结合在SystemC 系统设计中提到的Y-chart，本文将讨论在 Behavior 层面的系统建模：MoCs (Model of Computation)，希望对 DOL 的建模原理有一定认识：

　To model streaming applications, the dataflow process network model of computation [Lee and Parks 1995], a subclass of Kahn process networks [Kahn 1974], has been adopted in the DOL design flow.

　什么是dataflow process network？Kahn process networks又是什么？接下来我们将一一论述。　

Model of System（系统建模）

传统模型不能满足后续的 Requirements
- Von Neumann Model
- Thread-based Concurrency Models
Requirements for Model for Embedded Systems
- Modularity: Systems specified as a composition of objects
- Represent hierarchy: Humans not capable to understand systems containing more than a few objects
  - Behavioral hierarchy: like statements->procedures->programs
  - Structural hierarchy: like transistors->gates->processors->printed circuit
- Concurrency, synchronization and communication
- Represent timing behavior/requirements
  - Timing is essential for embedded systems!
  - Four types of timing specs required [Burns, 1990]
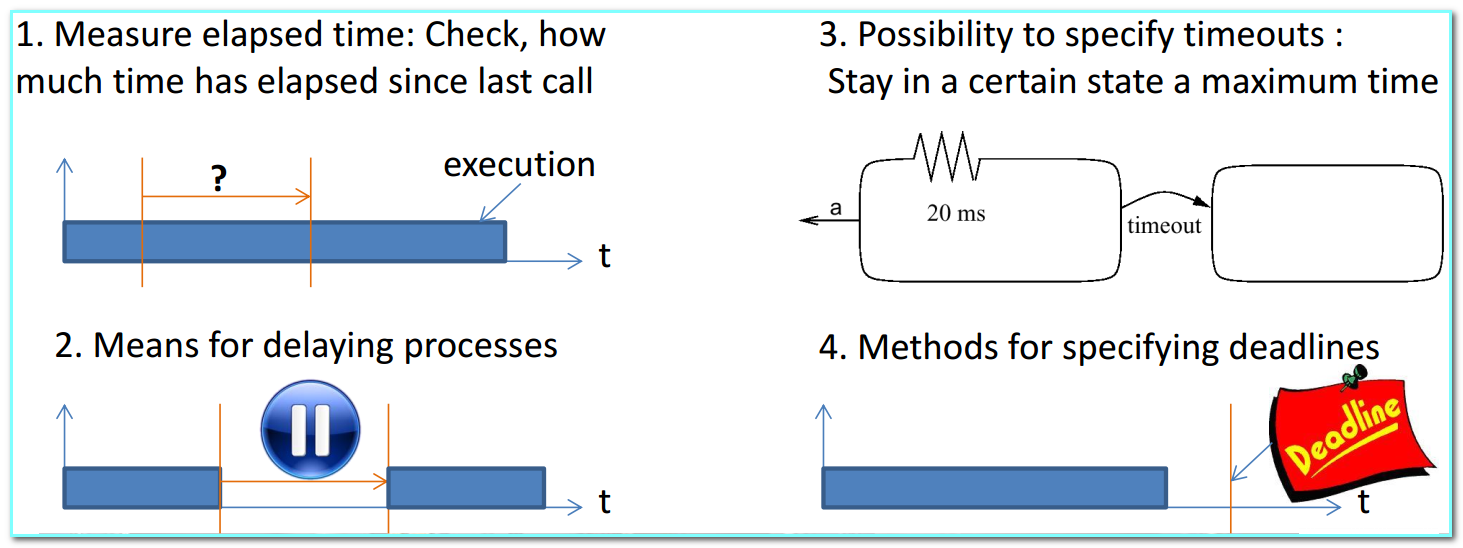
- Represent state-oriented behavior: Required for reactive systems
- Represent dataflow-oriented behavior: Components send streams of data to each other
Model of Computation（满足 Requirements 的一些系统建模方法）
- StateCharts
- Data-Flow Models
  - Kahn Process Network
  - Synchronous Dataflow

State Charts

FSM → State Charts
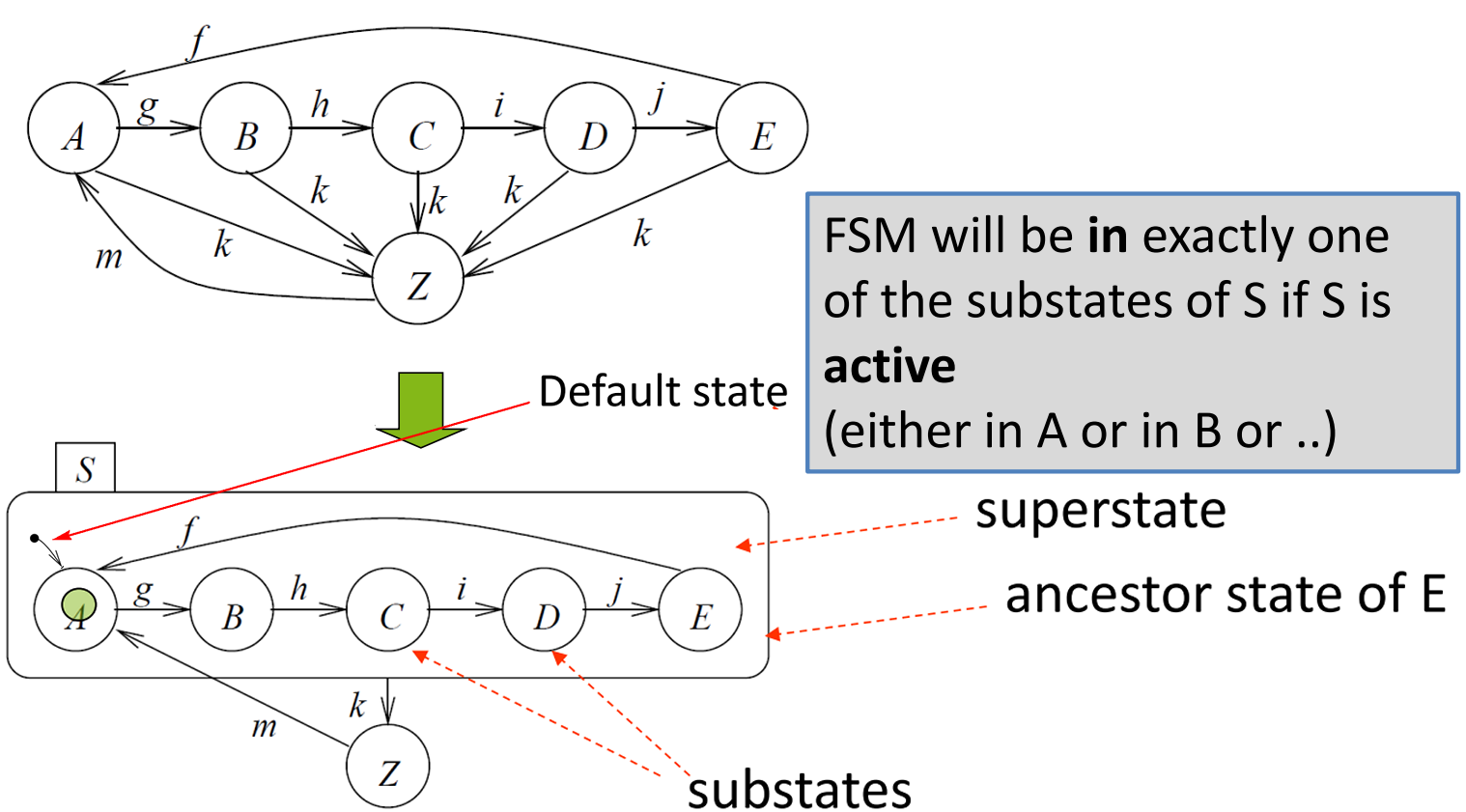
- Introducing Hierarchy
- Types of States
  - Current states of FSMs are also called active states
  - States which are not composed of other states are called basic states
  - States containing other states are called super-states
  - For each basic state s, the super-states containing s are called ancestor states
  - Super-states S are called OR-super-states, if exactly one of the sub-states of S is active whenever S is active.
- Default State Mechanism
Concurrency
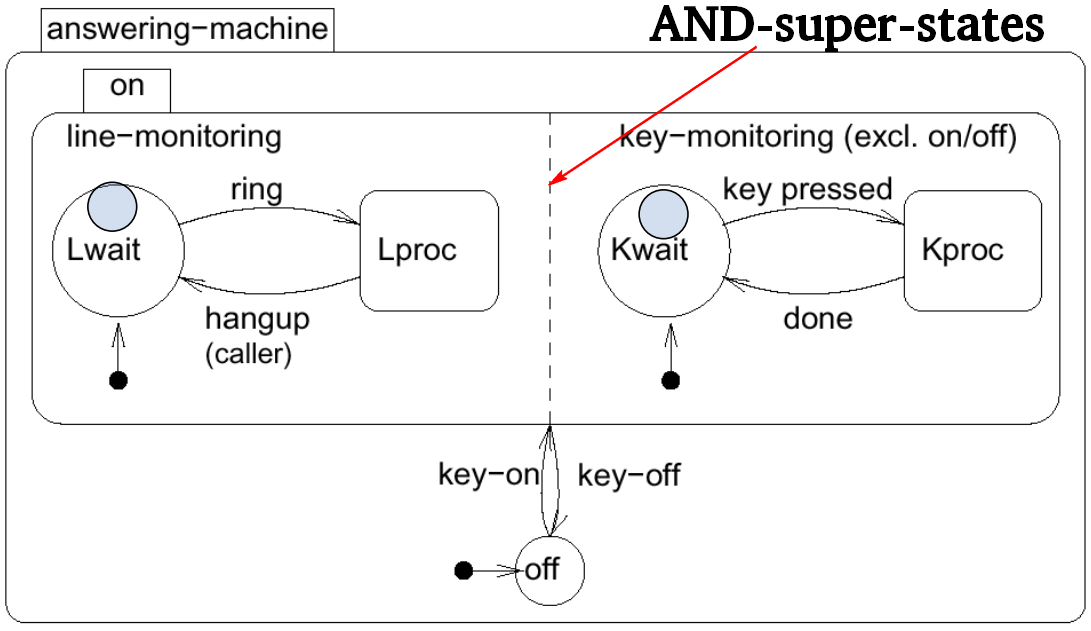
- AND-super-states: FSM is in all (immediate) sub-states of a super-state
Tree Representation of State Sets
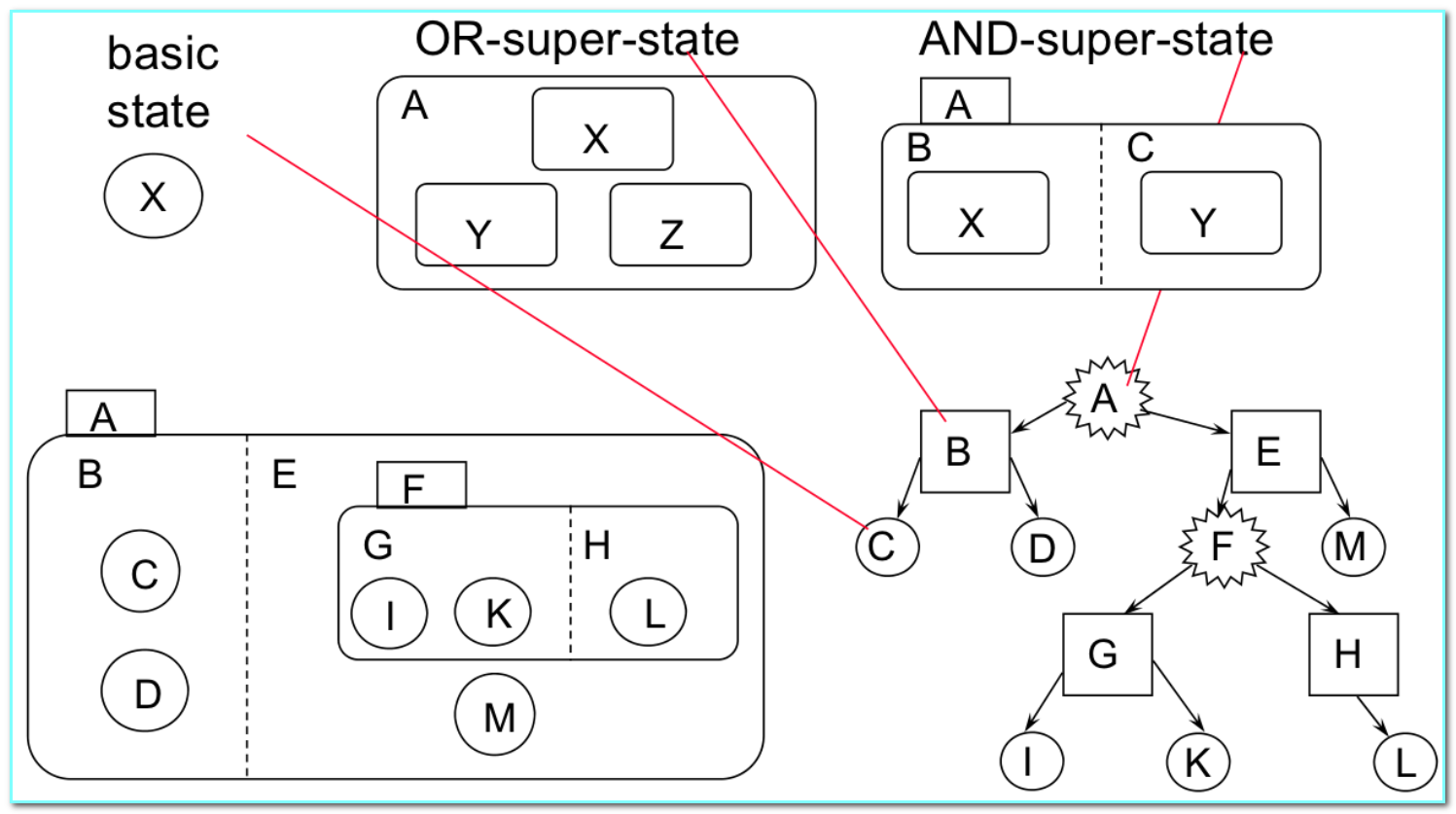
- Computation of State Sets（状态空间）：State Charts $\Longrightarrow$ FSM
  - basic states: state set = state
  - OR-super-states: state set = union of children
  - AND-super-states: state set = Cartesian product of children
    
    两个集合 $X$ 和 $Y$ 的笛卡尔积（Cartesian product），是所有可能的有序对组成的集合：
    $$X × Y = \verb|{| (x, y) \space | \space x \in X \wedge y \in Y \verb|}|$$
Representation of Computations
- Events
  - 有效性：only until the next evaluation of the model
  - Can be either internally or externally generated
  - “event” can be composed of several events: e1 and e2; e1 or e2; not e
- Conditions: refer to values of variables/states that keep their value until they are reassigned
- Actions
  - Can either be assignments for variables or creation of events
  - “action” can also be composed: (a1; a2), actions a1 and a2 are executed in parallel.
- All events, states and actions are globally visible

Data-Flow Models

All processes run “simultaneously”
Processes can be described with imperative code (Host Language, e.g. C/C++/Java/…)
Processes can only communicate through buffers, network description with Coordination Language, e.g. XML
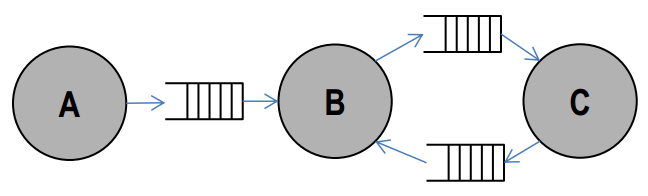
Sequence of read tokens is identical to the sequence of written tokens
Appropriate for applications that deal with streams of data
- Fundamentally concurrent: maps easily to parallel hardware
- Perfect fit for block-diagram specifications (control systems, signal processing)
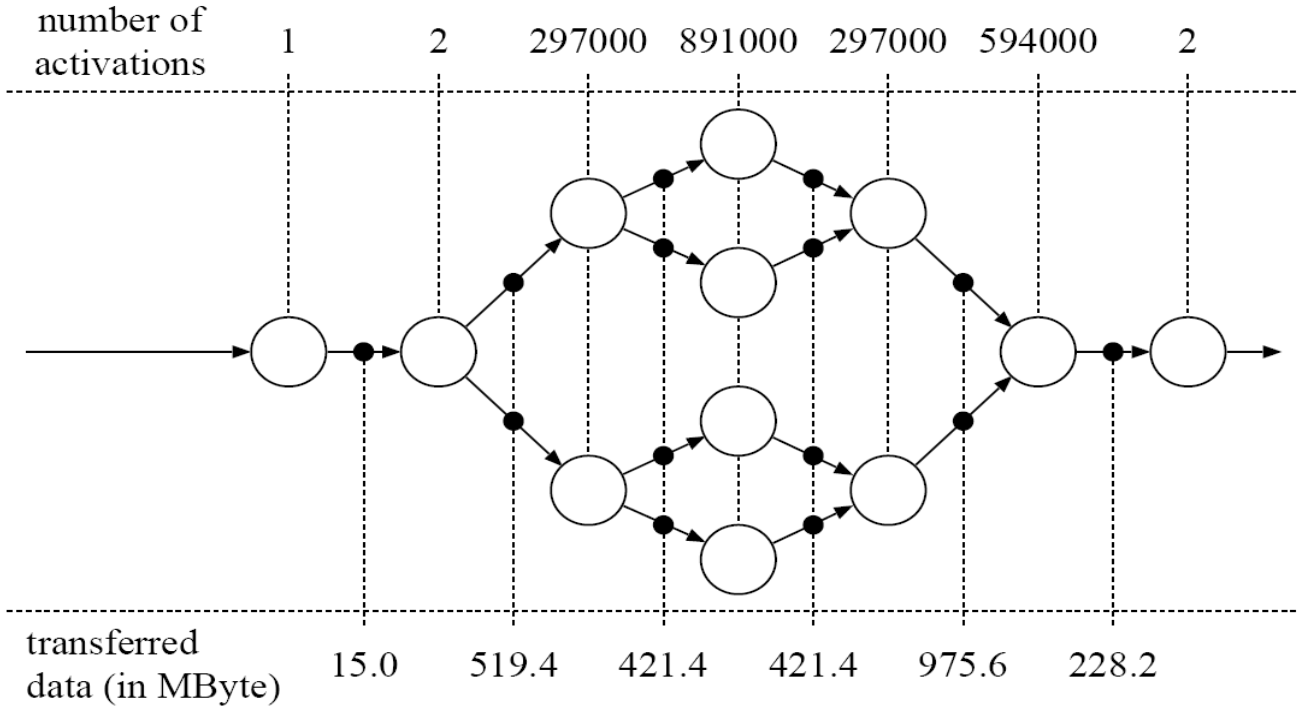
  Example: MPEG-2 Video Decoder
- Matches well current and future trend towards multimedia applications
下面详细介绍两种 Data-Flow Models：KPN 以及它的一种变种 SDF。

Kahn Process Network (KPN)

Proposed by Kahn in 1974 as a general-purpose scheme for parallel programming
- FIFO buffers（管道无穷大）: infinite size
- Blocking-read（阻塞读）: destructive and blocking (reading an empty channel blocks until data is available)
- Non-blocking-write（非阻塞写）
- Unique attribute: determinate（确定性）
KPN 的 Determinacy（确定性）问题
- Random vs Determinate: A system is random if the information known about the system and its inputs is not sufficient to determine its outputs
- Define the history of a channel to be the sequence of tokens that have been both written and read. A process network is said to be determinate if the histories of all channels (output channels) depend only on the histories of the input channels.
- Importance
  - Functional behavior（MoCs 是行为级层面的系统建模） is independent of timing (scheduling, communication time, execution time of processes)
  - Separation of functional properties and timing
- Proof of Determinism
  - monotonic（单调性）$\Longrightarrow$ determinate（确定性的严格证明）
    - 网络中的每个进程都是单调的，则整个网络也是单调的：A network of monotonic processes itself defines a monotonic process.
    - 一个单调的网络自然满足确定性：A monotonic process is clearly determinate
      如何证明进程的单调性？
      　① Formal definition
      
      input/output sequence (stream): $X = [x_1, x_2, x_3, …]$ （单个 channel）
      
      p-tuple of sequences: $\mathbf{X} = [X^1, X^2, X^3, …] \in S$（多个 channel）
      
      prefix ordering: $[x_1] \subseteq [x_1, x_2] \subseteq [x_1, x_2, x_3]$
      
      process: $F = S_{in} \to S_{out}$，输入 $\mathbf{X} \in S_{in}$，输出 $F(\mathbf{X}) \in S_{out}$
      
      　② $\mathbf{X} \subseteq \mathbf{X’} \Rightarrow F(\mathbf{X}) \subseteq F(\mathbf{X’})$ $\Longrightarrow$ monotonic process
      
      ordered set of sequences $\mathbf{X} \subseteq \mathbf{X’}$
      
      输入 sequences 互为 ordered set，输出 sequences 也互为 ordered set，那么进程是单调的
      　③ 如何证明：sequences 互为 ordered set
      
      证明：$ \forall X^i \subseteq X’^i \Rightarrow \mathbf{X} \subseteq \mathbf{X’}$
  - 反证法简单证明 $\Longrightarrow$ non-monotonic behavior（output 不仅取决于 input，还跟时间相关）$\Longrightarrow$ non-determinate
实例 (A Kahn Process Network): prints an alternating sequence of 0’s and 1’s
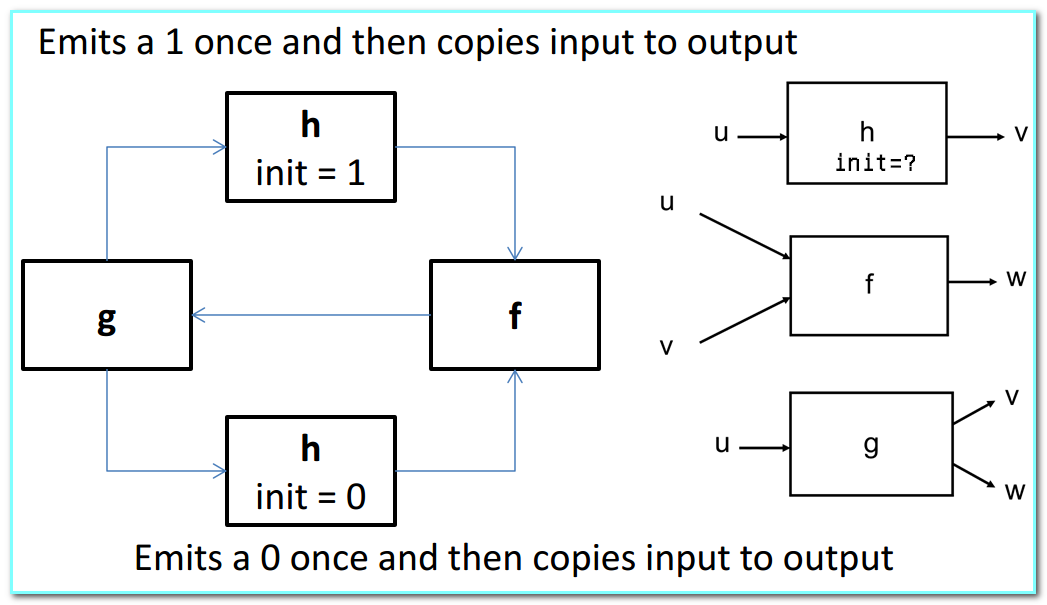
- Process h sends initial value, then passes through values

process h(in int u, out int v, int init) {
  int i = init;
  send(i, v);
  for(;;) {
    i = wait(u);
    send(i, v);
  }
}

Process falternately reads from u and v, prints the data value, and writes it to w

process f(in int u, in int v, out int w) {
  int i;
  bool b = true;
  for(;;) {
    i = b ? wait(u) : wait(v);
    printf("%i\n", i);
    send(i, w);
    b = !b;
  }
}

Process g reads from u and alternately copies it to v and w

process g(in int u, out int v, out int w) {
  int i;
  bool b = true;
  for(;;) {
    i = wait(u);
    if(b) {
      send(i, v);
    }
    else {
      send(i, w);
    }
    b = !b;
  }
}

整个 KPN 网络的单线程 Java 实现

KPN.java

package test;
 
import java.util.LinkedList;
import java.util.Queue;
 
public class KPN {
  Queue<Integer> chan1 = new LinkedList<Integer>();
  Queue<Integer> chan2 = new LinkedList<Integer>();
  Queue<Integer> chan3 = new LinkedList<Integer>();
  Queue<Integer> chan4 = new LinkedList<Integer>();
  Queue<Integer> chan5 = new LinkedList<Integer>();
  
  private int counter = 0;
  
  class h1 {
    private int init=1;
    h1(){
      chan1.add(init);
    }
    void run(){
      if(chan4.size()>0){
        int tmp = chan4.remove();
        chan1.add(tmp);
      }
    }
  }
  
  class h0 {
    private int init=0;
    h0(){
      chan2.add(init);
    }
    void run(){
      if(chan5.size()>0){
        int tmp = chan5.remove();
        chan2.add(tmp);
      }
    }
  }
  
  class g {
    private boolean write_up = true;
    void run(){
      if(chan3.size()>0){
        int tmp = chan3.remove();
        System.out.println("Output is: "+tmp+" at "+counter++);
        if(write_up){
          chan4.add(tmp);
        }
        else{
          chan5.add(tmp);
        }
        write_up = !write_up;
      }
    }
  }
  
  class f {
    private boolean read_up = true;
    void run(){
      if(read_up){
        if(chan1.size()>0){
          int tmp = chan1.remove();
          chan3.add(tmp);
          read_up = !read_up;
        }
      }
      else{
        if(chan2.size()>0){
          int tmp = chan2.remove();
          chan3.add(tmp);
          read_up = !read_up;
        }
      }
    }
  }
  
  h1 h1_;
  h0 h0_;
  f f_;
  g g_;
  
  KPN(){
    int i;
    // Test 1:
    /* initialize the channel and processes. */
    chan1.clear();
    chan2.clear();
    chan3.clear();
    chan4.clear();
    chan5.clear();
    h1_ = new h1();
    h0_ = new h0();
    f_ = new f();
    g_ = new g();
    System.out.println("Order 1:   h1, h0, f, g");
    for(i=0; i<100; ++i){
      h1_.run();
      h0_.run();
      f_.run();
      g_.run();
    }
    
    // Test 2:
    /* initialize the channel and processes. */
    chan1.clear();
    chan2.clear();
    chan3.clear();
    chan4.clear();
    chan5.clear();
    h1_ = new h1();
    h0_ = new h0();
    f_ = new f();
    g_ = new g();
    System.out.println("Order 2:   h1, h1, h1, g, f, h0, h0");
    for(; i<200; ++i){
      h1_.run();
      h1_.run();
      h1_.run();
      g_.run();
      f_.run();
      h0_.run();
      h0_.run();
    }
    // Test 3:
    /* initialize the channel and processes. */
    chan1.clear();
    chan2.clear();
    chan3.clear();
    chan4.clear();
    chan5.clear();
    h1_ = new h1();
    h0_ = new h0();
    f_ = new f();
    g_ = new g();
    System.out.println("Order 3:  f, f, g, h1, h0, h1, h0, h0, g");
    for(; i<300; ++i){
      f_.run();
      f_.run();
      g_.run();
      h1_.run();
      h0_.run();
      h1_.run();
      h0_.run();
      h0_.run();
      g_.run();
    }
    
    // Test 4:
    /* initialize the channel and processes. */
    chan1.clear();
    chan2.clear();
    chan3.clear();
    chan4.clear();
    chan5.clear();
    h1_ = new h1();
    h0_ = new h0();
    f_ = new f();
    g_ = new g();
    System.out.println("Order 4:   g, h0, h1, f");
    for(; i<400; ++i){
      g_.run();
      h0_.run();
      h1_.run();
      f_.run();
    }
    
    // Test 5:
    /* initialize the channel and processes. */
    chan1.clear();
    chan2.clear();
    chan3.clear();
    chan4.clear();
    chan5.clear();
    h1_ = new h1();
    h0_ = new h0();
    f_ = new f();
    g_ = new g();
    System.out.println("Order 5: g, g, g, h0, h1, f");
    for(; i<500; ++i){
      g_.run();
      g_.run();
      g_.run();
      h0_.run();
      h1_.run();
      f_.run();
    }
  }
  
  public static void main(String[] args){
    new KPN();
  }
}

整个 KPN 网络的多线程 Java 实现

KPN_multithread.java

package test;
 
import java.util.LinkedList;
import java.util.Queue;
import java.util.concurrent.locks.Lock;
import java.util.concurrent.locks.ReentrantLock;
 
public class KPN {
  private Lock lock = new ReentrantLock();
  
  private Queue<Integer> chan1 = new LinkedList<Integer>();
  private Queue<Integer> chan2 = new LinkedList<Integer>();
  private Queue<Integer> chan3 = new LinkedList<Integer>();
  private Queue<Integer> chan4 = new LinkedList<Integer>();
  private Queue<Integer> chan5 = new LinkedList<Integer>();
  private int counter=0;
  
  class h implements Runnable{
    Queue<Integer> in, out;
    private int init;
    
    h(Queue<Integer> in, Queue<Integer> out, int init){
      this.in = in;
      this.out = out;
      this.init = init;
      out.add(this.init);
    }
    
    @Override
    public void run() {
      while(true){
        lock.lock();
        try {
          if(in.size()>0){
            int tmp = in.remove();
            out.add(tmp);
          }
        } finally {
          lock.unlock();
        }
      }
    }
  }
  
  class f implements Runnable{
    Queue<Integer> in_up, in_down, out;
    private boolean read_up = true;
    f(Queue<Integer> in_up, Queue<Integer> in_down, Queue<Integer> out){
      this.in_up = in_up;
      this.in_down = in_down;
      this.out = out;
    }
    @Override
    public void run() {
      while(true){
        lock.lock();
        try {
          if(read_up) {
            if(in_up.size()>0){
              int tmp = in_up.remove();
              read_up = !read_up;
              out.add(tmp);
            }
          }
          else {
            if(in_down.size()>0){
              int tmp = in_down.remove();
              read_up = !read_up;
              out.add(tmp);
            }
          }
        }finally {
          lock.unlock();
        }
      }
    }
  }
  
  class g implements Runnable{
    Queue<Integer> in, out_up, out_down;
    private boolean write_up = true;
    
    g(Queue<Integer> in, Queue<Integer> out_up, Queue<Integer> out_down){
      this.in = in;
      this.out_up = out_up;
      this.out_down = out_down;
    }
    
    @Override
    public void run() {
      while(true){
        lock.lock();
        try {
          if(in.size()>0){
            int tmp = in.remove();
            if(counter<50)
              System.out.println("Output is: "+tmp+" at "+(++counter));
            if(write_up){
              out_up.add(tmp);
            }
            else{
              out_down.add(tmp);
            }
            write_up = !write_up;
          }
        } finally {
          lock.unlock();
        }
      }
    }
  }
  
  KPN(){
    h h1 = new h(chan4, chan1, 1);
    h h0 = new h(chan5, chan2, 0);
    g g_ = new g(chan3, chan4, chan5);
    f f_ = new f(chan1, chan2, chan3);
    /*Order1: h1 h0 f g
		new Thread(h1).start();
		new Thread(h0).start();
		new Thread(g_).start();
		new Thread(f_).start();
		*/
    /*Order2: h1 h1 h1 g f h0 h0
		new Thread(h1).start();
		new Thread(h1).start();
		new Thread(h1).start();
		new Thread(g_).start();
		new Thread(f_).start();
		new Thread(h0).start();
		new Thread(h0).start();
		*/
    /*Order3: f f g h1 h0 h1 h0 h0 g*/
    new Thread(f_).start();
    new Thread(f_).start();
    new Thread(g_).start();
    new Thread(h1).start();
    new Thread(h0).start();
    new Thread(h1).start();
    new Thread(h0).start();
    new Thread(h0).start();
    new Thread(g_).start();
  }
  
  public static void main(String[] args){
    new KPN();
  }
}

Scheduling Kahn Networks $\Longrightarrow$ KPN 网络难以调度
- 系统运行顺畅：Challenge is running processes without accumulating tokens and without producing a deadlock
- Tom Parks’ Algorithm: Schedules a Kahn Process Network in bounded memory
  - Parks’ algorithm expensive and fussy to implement
  - Difficult to schedule because of need to balance relative process rates

Synchronous Dataflow (SDF)

　从上面论述，我们了解到，KPN 需要infinite buffer size，另外，它难以调度，这些都是实际应用中几乎不可能解决的问题；相比之下，SDF 则更多运用在实际场景中。

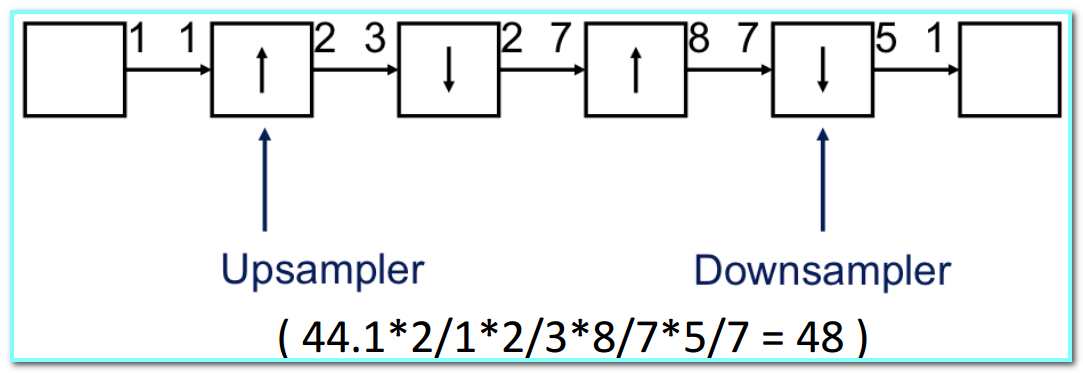
Example: DAT-to-CD rate converter (converts a 44.1 kHz sampling rate to 48 kHz)

KPN $\rightarrow$ SDF
- Restriction of Kahn Networks to allow compile-time scheduling
  - Each process reads and writes a fixed number of tokens each time it fires
  - Firing is an atomic process
调度策略 $\Longrightarrow$ the schedule can be executed repeatedly without accumulating tokens in buffers
- Solving the Balancing Equation $\Longrightarrow$ Establish relative execution rates
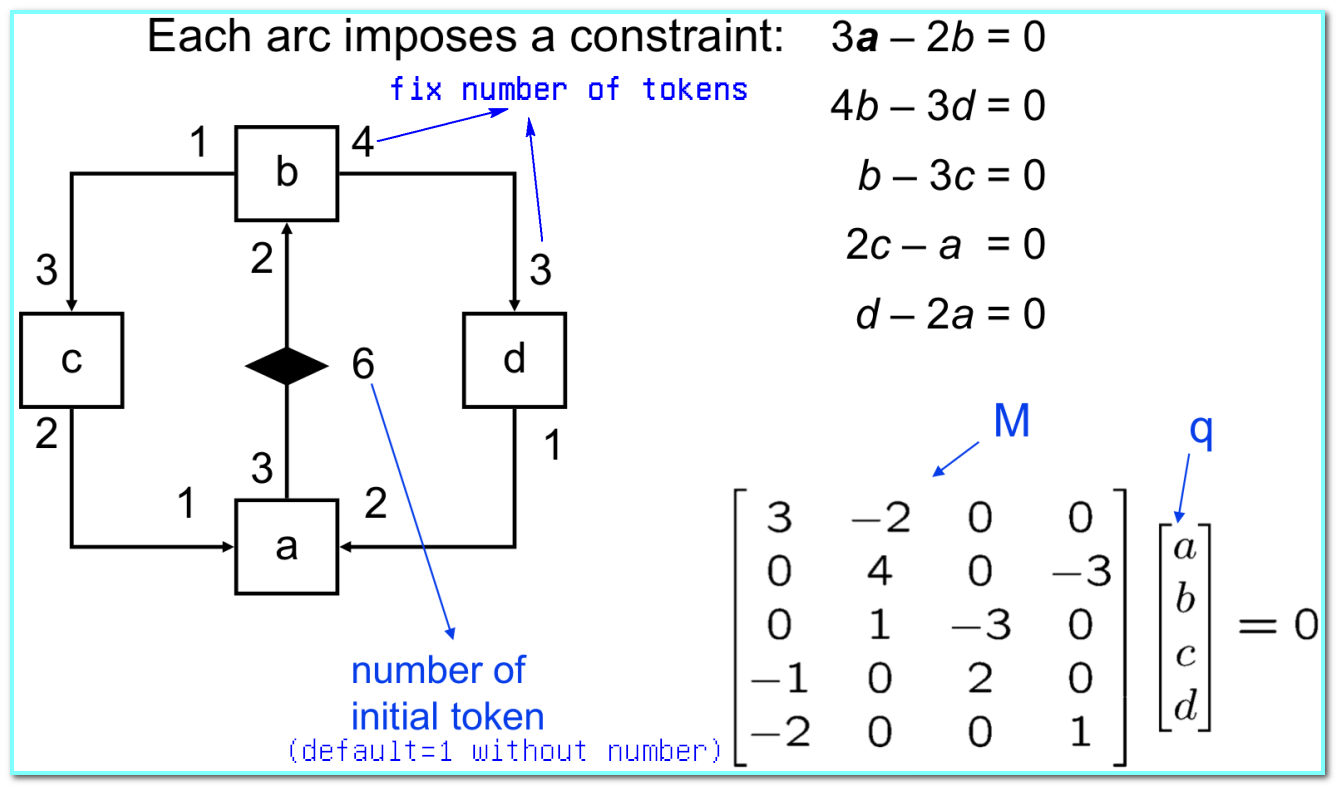
  - 对$n$ 个进程构成的 SDF 中的各条 channel 建立约束方程，得到 topology matrix（拓扑矩阵）M
  - 解线性方程组 $M \overrightarrow{q} = 0$，得到每个进程在每个周期中的运行次数 $\overrightarrow{q}$
    - rank(M) = n-1: A connected SDF graph（连通且相容的 SDF）, then there exists a unique smallest positive integer solution $\overrightarrow{q}$ （存在周期性调度，最小正整数为对应的进程在每个周期中的运行次数）
    - rank(M) < n-1: Disconnected systems（不连通的 SDF）, then have two- or higher-dimensional solutions （存在某些进程可以独立运行，它们与整个系统脱离）
    - rank(M) = n: Inconsistent systems（不相容的 SDF）, then only have the all-zeros solution （不存在可能的调度策略去运行，因为总会出现无限累积）
- Determine Periodic Schedule
  - Consistent Rates Not Enough: ① Rates do not avoid deadlock; ② Add an initial token (delay) on one of the channels $\Longrightarrow$ 在满足每个进程的运行次数下，决定一个周期内所有进程的运行顺序。
  - Systems often have many possible schedules. How can we use this flexibility
    - Reduced code size (loop structure, hierarchy): BBBCDDDDAA$\Longrightarrow$(3B)C(4D)(2A)
    - Reduced buffer sizes: 虽然整个系统在每次周期运行后，进程间的 channels 都不会出现数据积累，但每个周期运行过程中，每条 channel 需要有足够大小的 buffer 用于转存数据。

References

本文标题:嵌入式系统导论[03] Model of Computation

文章作者:Gary

发布时间:2017-10-24, 12:50:14

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/10/24/TACouses_ES2017_MoCs/