Books:数字图像处理(冈萨雷斯)
Codes:https://github.com/Durant35/Courses/tree/master/dip
第2章 数字图像基础
- 取样和量化
- 空间和灰度分辨率
- 图像内插
- 像素间的一些基本关系
- $N_4(p)$;$N_8(p) = N_4(p) + N_D(p)$(对角像素) 4领域/8领域
- 距离度量 $D_e(p, q)$
- 城市街区距离:$p(x, y)$;$q(s, t)$;$D_4(p, q) = |x-s| + |y-t|$
- 棋盘距离:$p(x, y)$;$q(s, t)$;$D_4(p, q) = |x-s| + |y-t|$
- 邻接性:
- 4 邻接;8邻接:二义性(像素到另一个像素有多条路径)
- m 邻接:p是q的m邻接,首先p,q具有V中的数值;
-(i)p在$N_4(q)$中或
-(ii)p在$N_D(q)$且$N_4(p)∩N_4(q)$中没有V值(为空或不为空但没有V值)
- Path:从一个像素到另一个像素的一个像素序列
- 4-path:一个路径上的相邻像素互为4邻接
- 8-path:一个路径上的相邻像素互为8-neighbors
- 闭合通路:一个有限区域的边界形成一条闭合通路
第6章 彩色图像处理
- 人眼对彩色的敏感程度要远远高于对灰度级别的敏感程度
- CMY/CMYK(青色 深红色 黄色 黑色)$\begin{bmatrix} C\\ M \\Y \end{bmatrix} = \begin{bmatrix} 1 \\1 \\1\end{bmatrix} - \begin{bmatrix} R \\G \\B\end{bmatrix}$
- HSI(色调 饱和度 强度)
- 色调,饱和度和强度
- 色调(Hue):与光波的波长有关,它表示人的感官对不同颜色的感受
- 饱和度(Saturation):表示颜色的纯度,纯光谱色是完全饱和的
- 强度(Intensity):颜色的明亮程度
- 强度轴:$(0, 0, 0) \rightarrow (1, 1, 1) $
- 色调平面
- $强度轴 + 彩色点 \Rightarrow 三角面$
- $R(0°) \rightarrow G(120°) \rightarrow B(240°)$
- 饱和度(纯度)
- 纯色被白光稀释的程度
- 以与强度轴的距离为函数
- $RGB \rightarrow HSI$ RGB归一化到$[0, 1]$
- $ H[0, 360] = \begin{cases} \theta, &B \leq G \cr 360 - \theta, &B \gt G \end{cases} $,其中$ \theta = arccos\{\frac{\frac{1}{2}[(R-G)+(R-B])}{[(R-G)^2 + (R-B)(G-B)]^\frac{1}{2}} \}$
- $ S[0, 1] = 1 - \frac{3}{R+G+B}[min(R, G, B)] $,纯色值为 1
- $ I[0, 1] = \frac{1}{3}(R + G + B) $,黑色值为 0/白色值为 1
- $HSI \rightarrow RGB$ $H[0, 360]; S[0, 1]; I[0, 1]$
- $ 0° \leq H \le 120°,\begin{cases} B = I(1-S) \cr R = I[1 + \frac{ScosH}{cos(60° - H)}] \cr G = 3I - (R+B) \end{cases} $
- $ 120° \leq H \le 240°,H = H - 120°,\begin{cases} R = I(1-S) \cr G = I[1 + \frac{ScosH}{cos(60° - H)}] \cr B = 3I - (R+G) \end{cases} $
- $ 240° \leq H \le 360°,H = H - 240°,\begin{cases} G = I(1-S) \cr B = I[1 + \frac{ScosH}{cos(60° - H)}] \cr R = 3I - (G+B) \end{cases} $
- HSI 模型更符合人眼对颜色的解释,该模型可以在彩色图像中从携带的彩色信息中将色度信息(色调和饱和度)和强度信息的分量分开
- 色调,饱和度和强度
- 伪彩色:基于一种指定的规则对灰度值赋以颜色的处理
- 一幅单色图像
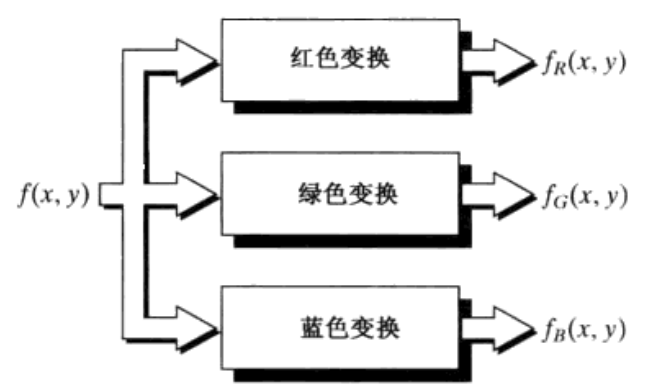
- 多幅单色图像
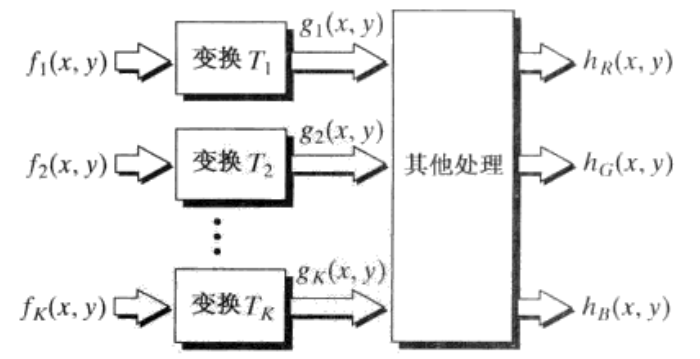
- 一幅单色图像
- 全彩色图像:全彩色传感器采集的图像
$ \begin{cases} 分别处理每一个向量 \cr 直接处理彩色像素 \end{cases} \Longleftarrow[条件] \begin{cases} ①处理必须对于向量和标量都可用 \cr ②对向量的每一个分量的操作对于其他分量必须是独立的 \end{cases} $ - 独立于设备的彩色模型:
CIEL*a*b*(亮度;红减绿;绿减蓝)- 没有可直接显示的格式(需要变换到另外的彩色空间),但其色域包括整个可见光谱,并可以准确地表示任何显示设备,打印设备或输入设备的颜色
- 通常的彩色显设备是不能显示自然界所有颜色,仅限于该显示器的三原色所构成的三角形内,不能完全覆盖整个色度图
- 色调范围(主调类型):颜色强度的基本分布
- 高主调:高(亮)强度处
- 中主调
- 低主调:低(暗)亮度处
- 单独对彩色图像的分量进行直方图均衡通常是不明智的,应当均匀地展开这种彩色灰度,而保持彩色本身(即色调)不变$ \Rightarrow $ 转换到HSI彩色空间进行直方图处理
- 彩色图像的噪声内容在每个彩色通道中具有相同的特性,但噪声对不同的彩色通道所造成的影响不同
- 彩色图像平滑
- 领域平均平滑可以在每个彩色平面的基础上执行,其结果与使用RGB彩色向量执行平均效果是相同的
- 彩色图像锐化
- 一个向量的拉普拉斯被定义为一个向量,其分量等于输入向量的各个标量分量的拉普拉斯
第3章 灰度变换与空间滤波
- 空间域 vs 变换域
- 空间域:直接以图像中的像素操作为基础
- 空间域处理$ \begin{cases} 灰度变换:在图像的单个像素上操作,主要以对比度/阈值处理为目的(图像增强/图像分割) \cr 空间滤波:图像中每一个像素的领域处理 \end{cases} $
- 变换域:先把一幅图像变换到变换域,在变换域中进行处理,然后反变换把处理的结果返回到空间域
- 点处理技术 vs 领域处理技术
- 图像增强
- 对图像进行加工,使其结果对于特定的应用比原始图像更合适的一种处理
- “特定”:面向问题,没有通用的“理论”;效果没办法量化
- 基本的灰度变换函数
- 图像反转
- $ S = L - 1 - r,(r \in [0, L-1])$
- 增强嵌入在一幅图像的暗区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时
- 对数变换
- $ S = clog(1+r),(c为常数,r \geq 0) $
- 扩展图像中的暗像素的值,同时压缩更高灰度级的值 $\Longleftrightarrow$ 反对数
- 压缩像素值变化较大的图像的动态范围,如傅里叶频谱$(0,10^6)\Longrightarrow$ 图像显示系统通常不能如实地再现如此大的范围
- 幂律(伽马)变换
- $ S = cr^{\gamma},(c,\gamma为正常数) $
- 参数性质
- $ \gamma \gt 1 $,(越大越)扩展高灰度级值(亮部的细节)
- $ \gamma \lt 1 $,(越小越)扩展低灰度级值(暗部的细节)
- 有些计算机系统内置部分伽马校正,因为计算机屏幕内部自带伽马校正,改变伽马值不仅会改变亮度,而且会改变彩色图像中的 R,G,B 比率
- 整体偏暗的对比度增强
- “冲淡”外观的灰度级压缩
- 分阶级性变换函数
- 对比度拉伸:特定灰度级范围斜率变化大(低于 k 的灰度级更暗,高于 k 的灰度级更亮)
- 灰度级分层:特定灰度级范围的亮度进行不同赋值(例如二值化)
- 比特平面分层
- $ \begin{cases} 高阶比特:视觉上很重要的大部分数据 \cr 低阶比特:更精细的灰度细节 \end{cases} $ $\Longrightarrow$ 图像压缩:4个高阶比特平面将允许我们从可接受的细节来重建原图像
- 图像反转
- 直方图处理
- 概述
- 灰度级范围为$[0, L-1]$的数字图像的直方图:$h(r_k) = n_k$,$r_k$ 是第 k 级灰度值,$n_k$ 是 $r_k$ 的像素个数
- 归一化:$p(r_k) = \frac{n_k}{MN}$,灰度级 $r_k$ 在图像中出现的概率
- 图像的直方图反映了图像的明暗程度以及对比强度,对比度适中的图像通常具有均匀分布的直方图
- 低对比度图像具有较窄的直方图,且集中于灰度级的中部;高对比度图像中直方图的分量覆盖了很宽的灰度级范围,而且像素的分布没有太不均匀
- 若一幅图像的像素倾向于占据整个可能灰度级并且分布均匀,则该图像会有高对比度的外观并展示灰色调的较大变化
- 直方图均衡化
- 直方图均衡化变换(直方图线性变换)
$ S_k = T(r_k) = (L-1) \sum_{j=0}^k p_r(r_j) = \frac{L-1}{MN} \sum_{j=0}^k n_j,k=0, 1, 2, 3, …, L-1$ - “自动的”:因为图像有相同的内容,直方图均衡导致的对比度增强足以补偿图像在视觉上难以区分灰度级的差别
- 直方图均衡化变换(直方图线性变换)
- 直方图匹配(直方图规定化)
- Histogram Matching(Specification):是指对一副图像进行变换,使其直方图与另一幅图像的直方图或特定函数形式的直方图匹配;是用户处理图像后,产生特殊直方图的方法
- 步骤
- 计算直方图 $p_r(r)$,获取直方图均衡变换 $S_k$,把 $S_k$ 四舍五入到 $[0, L-1]$ 范围内的整数
- 计算变换函数:$G(z_q) = (L-1) \sum_{i=0}^{q} p_z(z_i)$,其中 $q=0, 1, 2, 3, …, L-1$,$p_z(z_i)$ 是规定的直方图
- 把 G 的值四舍五入到 $[0, L-1]$ 范围整数,存储在查找表中
- 满足最接近 $S_k$ 的 $G(z_q)$ 的 $z_q$ 值即为直方图规定化后的像素值(当满足给定的 $S_k$ 的 $z_q$ 值多于一个时,选择最小的 $z_q$ 值)
- 局部直方图均衡化:增强小区域的细节
- 在图像增强中使用直方图统计
- 统计量
- 平均灰度:$m = \sum_{i=0}^{L-1} r_i p(r_i)$ 或(取样均值)$m = \frac{1}{MN} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y)$
- 灰度方差:$\mu_2(r) = \sum_{i=0}^{L-1} (r_i - m)^2 p(r_i)$ 或(取样方差)$\sigma^2 = \frac{1}{MN} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} [f(x, y) - m]^2$
- n阶矩:$\mu_{n}(r) = \sum_{i=0}^{L-1} (r_i - m)^n p(r_i)$
- 根据统计量判断
- 判断一个区域在点 $(x, y)$ 是暗还是亮:$m_{S_{xy}} \leq km_G$,其中 $m_{S_{xy}}$ 为局部平均灰度,$m_G$ 为全局均值
- 判断一个区域的对比度是否可作为低对比度区域:$k_1 \sigma_G \leq \sigma_{S_{xy}} \leq k_2 \sigma_G$(标准差为 0 的区域需排除)
- 统计量
- 概述
- 空间滤波(线性空间滤波器;非线性空间滤波器)
- 一个邻域(典型的是一个较小的矩形;奇数尺寸,最小 $3x3$)
- 对该邻域包围的图像像素执行的预定义操作
- 一个 mxn 的滤波器 $\omega(x, y), m=2a+1, n=2b+1$
- 操作:$g(x, y) = \sum_{s=-a}^a \sum_{t=-b}^b \omega(s, t)f(x+s, y+t) $(一般空间滤波器旋转180°后保持不变)
- 相关 vs 卷积
- 1D
- 要求:n 必须满足 $g(n)$ 完全滑过 $f(n)$
- 卷积需要将 $g(n)$ 旋转180°(怎么补零?)$ \Longleftarrow \begin{cases} 卷积:(f \otimes g)[n] = \sum_{m=0}^{N-1} f(m)g(n-m) \cr 相关:(f \circ g)[n] = \sum_{m=0}^{N-1} f(m)g(n+m) \end{cases} $
- 2D
- 对所有位移变量 x 和 y 求值,以便 $\omega$ 的所有元素访问 $f$ 的每一个像素
- $ \Longrightarrow \begin{cases} 卷积:\omega (x, y) \otimes f(x, y) = \sum_{s=-a}^a \sum_{t=-b}^b \omega(s, t)f(x-s, y-t) \cr 相关:\omega (x, y) \circ f(x, y) = \sum_{s=-a}^a \sum_{t=-b}^b \omega(s, t)f(x+s, y+t) \end{cases} $
- 1D
- 平滑空间滤波器:用于模糊处理 $\Rightarrow$ 降低噪声
- 平滑线性滤波器(均值滤波器):响应是包含在滤波器模板邻域内的像素的简单平均值
- 降低了图像灰度的“尖锐”变化,比如典型的随机噪声就由灰度级急剧变化组成
- 图像边缘也是由图像灰度尖锐变化带来的特性 $\Rightarrow$ 边缘模糊的负面效应
- 盒状滤波器 vs 加权平均
- 随着距中心点的距离的增加而减小系数值的加权策略 $\Rightarrow$ 降低模糊
$g(x, y) = \frac{\sum_{s=-a}^a \sum_{t=-b}^b \omega(s, t)f(x+s, y+t)}{\sum_{s=-a}^a \sum_{t=-b}^b \omega(s, t)}$ - 空间均值处理:模糊图像,较小物体的灰度与背景混在一起,较大物体变得像“斑点”而易于检测
- 随着距中心点的距离的增加而减小系数值的加权策略 $\Rightarrow$ 降低模糊
- 统计排序(非线性)滤波器
- 响应以滤波器包围的区域中所包含像素的排序为基础,使用统计排序结果决定的值代替中心像素的值
- 中值滤波器 最大值滤波器
- 锐化空间滤波器:突出灰度的过渡部分
- $ \begin{cases} 图像模糊:通过在空间域用像素邻域平均法实现 \Rightarrow 积分 \cr 锐化可以用空间微分来实现 \Rightarrow 增强边缘和其它突变(如噪声),而削弱灰度变化缓慢的区域 \end{cases} $
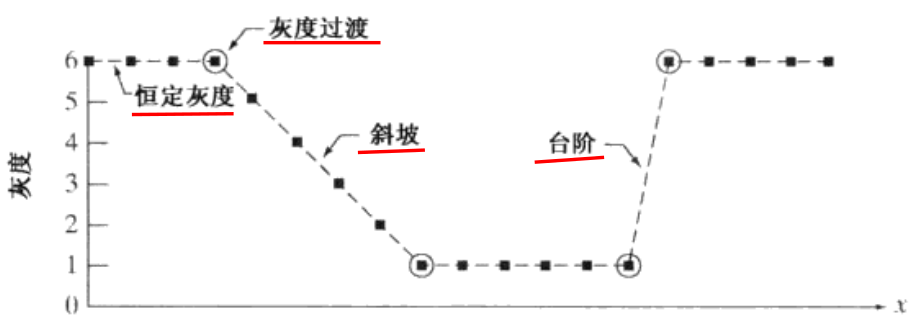
- 微分
- 一阶微分:$\frac{\partial f}{\partial x} = f(x+1) - f(x)$,用到下一个点,“预测未来”
- 二阶微分:$\frac{\partial^2 f}{\partial^2 x} = f(x+1) + f(x-1) - 2f(x)$
- 数字图像中的边缘在灰度上常常类似于斜坡过渡,一阶微分会产生较粗的边缘,二阶微分产生由零分开的一个像素宽的双边缘。二阶微分在增强细节方面要比一阶微分好的多,适合锐化图像
- 拉普拉斯算子:$\nabla^2 f = \frac{\partial^2 f}{\partial^2 x} + \frac{\partial^2 f}{\partial^2 y}$
- 是一个各向同性滤波器:响应与作用的图像的突变方向无关;将原图像旋转后进行滤波处理给出的结果与先滤波再旋转的结果相同
- $\nabla^2 f(x, y) = f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x, y)$
- 上面公式只是四种算子中的一个
$\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix}$ $\begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}$ $\begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix}$ $\begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{bmatrix}$ - 输入图像 $f(x, y)$,锐化后的图像 $g(x, y)$:$g(x, y) = f(x, y) + c[\nabla^2 f(x, y)]$,c 的符号与中心系数 $[f(x, y)]$ 的符号相反
- 任意阶微分都是线性操作,$\nabla^2 f(x, y)$ 也是一个线性算子
- 将原图像和拉普拉斯图像叠加,可以复原背景特性并保持拉普拉斯锐化处理的结果(强调灰度的突变,并不强调灰度缓慢变化的区域)
- 通过拉普拉斯变换增强了图像中灰度突变处的对比度,使图像中的细节部分得到了增强,并良好地保留了图像的基本色调
- $ \begin{cases} 图像模糊:通过在空间域用像素邻域平均法实现 \Rightarrow 积分 \cr 锐化可以用空间微分来实现 \Rightarrow 增强边缘和其它突变(如噪声),而削弱灰度变化缓慢的区域 \end{cases} $
- 非锐化掩蔽
- 从原图像中减去一幅非锐化(平滑/模糊过的)图像 $\bar{f}(x, y) \leftarrow$ 高斯滤波器模糊
- 非锐化模板:$g_{mask}(x, y) = f(x, y) - \bar{f}(x, y)$
- $g(x, y) = f(x, y) + k * g_{mask}(x, y)$
- $k = 1$:非锐化掩蔽
- $k \gt 1$:高提升滤波
- 梯度与 Sobel 算子
- 梯度
- $\nabla f = grad(f) = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}$
- $\nabla f $ 为向量,幅度值 $M(x, y) = mag(\nabla f) = \sqrt{g_x^2 + g_y^2}$,不是线性算子,因为做了平方和平方根操作
- $\Longrightarrow M(x, y) ≈|g_x| + |g_y|$,仍保留灰度的相对变化,虽然通常丢失了方向性
- Sobel 算子
- $M(x, y) ≈|(z_7 + 2z_8 + z_9) - (z_1 + 2z_2 + z_3)| + |(z_3 + 2z_6 + z_9) - (z_1 + 2z_4 + z_7)|$
- 矩阵形式:$\begin{bmatrix} z_1 & z_2 & z_3 \\ z_4 & z_5 & z_6 \\ z_7 & z_8 & z_9 \end{bmatrix}$ $\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$ $\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}$
- 梯度
- 应用多种互补的图像增强技术
- 拉普拉斯操作作为一种二阶微分算子在图像细节增强方面,它是最好的,但这会导致产生比梯度操作更多的噪声
- 梯度操作(Sobel 算子)对噪声和小细节响应要比拉普拉斯变换操作的响应弱,而且可以通过均值滤波器进行平滑而进一步降低
- 拉普拉斯图像与平滑处理后的梯度图像相乘,乘积会保留灰度变化强烈区域的细节,同时降低灰度变化相对平坦区域的噪声
- 具有重要边缘内容的梯度图像,边缘要比拉普拉斯图像突出,乘积的关键目的:强边缘的优势和可见噪声的减少
- 锐化/平滑过程从感知方法上没有影响图像灰度的动态变化,通过幂律变换可以增大锐化后图像的动态范围
第4章 频率域滤波
- 一维连续
- 傅里叶变换对
$ F(\mu) = \zeta\{f(t)\} = \int_{-\infty}^{\infty} f(t) e^{-j2\pi \mu t}\, dt$
$ f(t) = \zeta^{-1}\{F(\mu)\} = \int_{-\infty}^{\infty} F(\mu) e^{j2\pi \mu t}\, d\mu$ - 卷积
$ f(t) \bigotimes h(t) = \int_{-\infty}^{\infty} f(\tau) h(t- \tau) \, d\tau = F(\mu)H(\mu) = \sum_{n=-\infty}^{\infty}f(n\Delta T)h(t - n\Delta T)$
- 傅里叶变换对
- 一维离散
- $f(t)$ 的 M 个样本组成集合 $\{f_n\} = f(x)$
- $M$ 个复数离散值的傅里叶变换样本集合 ${f_m} = F(\mu)$
$ F(\mu) = \sum_{x=0}^{M-1} f(x) e^{-j2\pi \frac{\mu x}{M} },\mu = 0, 1, 2, …, M-1$
$ f(x) = \frac{1}{M}\sum_{\mu =0}^{M-1} F(\mu) e^{j2\pi \frac{\mu x}{M} },x = 0, 1, 2, …, M-1$
- 二维
- 连续
$ F(\mu, \nu) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-j2\pi(\mu t + \nu z)}\, dt\, dz$
$ f(t, z) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(\mu, \nu) e^{j2\pi(\mu t + \nu z)}\, d\mu \, d\nu$ - 离散
$ F(\mu, \nu) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j2\pi(\frac{\mu x}{M} + \frac{\nu y}{N})}$
$ f(x, y) = \frac{1}{MN}\sum_{\mu =0}^{M-1} \sum_{\nu =0}^{N-1} F(\mu, \nu) e^{j2\pi(\frac{\mu x}{M} + \frac{\nu y}{N})}$
- 连续
- 使用DFT时,图像和滤波器的大小必须相同
- $MxN$ 的图像 $f$
- 进行 $PxQ$ 填充成 $f_p$($P\geq2M-1, Q\geq2N-1$)
- $(-1)^{x+y}$ 乘以 $f_p$
- $f_p$ 的傅里叶变换(DFT)生成 $F_p$
- 滤波器扩容成 $PxQ$,关于中心对称化后生成 $H(u, v)$
- $H(u, v)F_p \Rightarrow G(u, v)$
- 计算 $G(u, v)$ 的 IDFT,得到 $\zeta^{-1}[G(u, v)]$
- 处理后得到图像 $g_p = \{ real[\zeta^{-1}[G(u, v)]] \}(-1)^{x+y}$
- 裁剪 $g_p$ 的前 M 行和前 N 列得到最终的结果
- 空间模板 [转换]$\Longrightarrow$ 频率域滤波器 $H(u, v)$
- $h(x, y)$ 扩充成 $h_p(x, y)$
- $(-1)^{x+y}$ 乘以 $h_p(x, y)$ 以便频率域滤波器“中心化”
- 计算上述结果的 DFT
- 滤波器 $H(u, v)$ 必须是纯虚函数,将得到的 DFT 实部置零
- $H(u, v)$ 等于 $(-1)^{x+y}$ 乘以上述结果,隐含着 $h(x, y)$ 被移到 $h_p(x, y)$ 的中心
- 傅里叶频谱
- 傅里叶频谱中心点对应于空间域的平均灰度或背景灰度
- 从中心点离开,低频信息对应慢变化的分量,如大体轮廓,背景等平滑部分
- 进一步离开中心点,较高频率对应变化越来越快的灰度级,如边缘,细节,噪声
第5章 图像复原与重建
- 图像退化/复原过程的模型
- $G(u, v) = H(u, v)F(u, v) + N(u, v)$
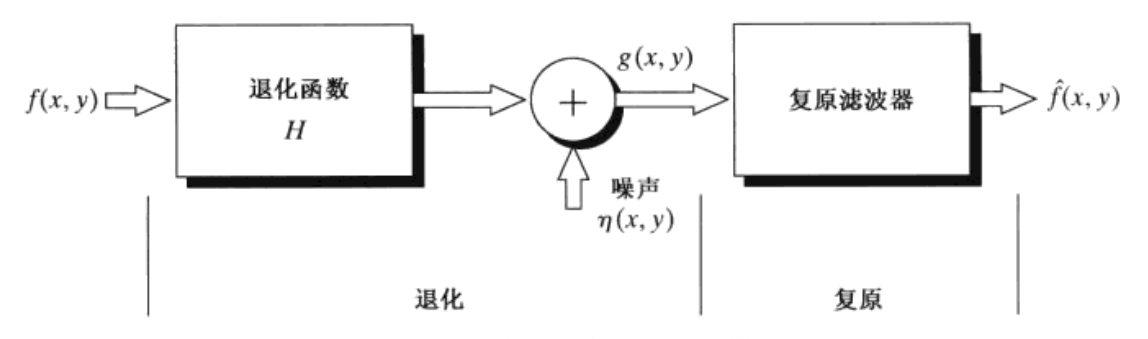
- $G(u, v) = H(u, v)F(u, v) + N(u, v)$
- 图像增强 vs 图像复原
- 图像增强主要是一个主观过程,首要目标是处理图像,使其比原始图像更适合于特定应用,如对比度增强
- 图像复原大部分过程是一个客观过程,利用退化现象的先验知识来重建或复原被退化的原始图像
- 噪声模型
- 高斯噪声

- 去噪:均值,中点
- 瑞利噪声

- 近似歪斜,比较胖
- 去噪:
- 伽马噪声

- 比较尖
- 去噪:
- 指数噪声

- 去噪:
- 均匀噪声

- 去噪:中点
- 脉冲噪声

- 去噪:谐波均值,逆谐波均值,中值,最大值/最小值
- 周期噪声
- 傅里叶共轭点,近似圆
- 去噪:低通,带通……
- 如何获取$ N(u, v) $?
- 在图像的平坦区域取一小块自图像做直方图,与已有的噪声模型作对比
- 高斯噪声
- 常见滤波器降噪情况
- 高斯或者均匀随机噪声 $ \Longleftarrow \begin{cases} 均值滤波平滑一幅图像中的局部变化,虽然模糊了结果,但降低了噪声 \cr 几何均值丢失的图像细节更少 \end{cases} $
- 谐波均值对盐噪声较好,不适用于椒噪声,善于处理像高斯噪声
- 逆谐波均值,$ Q \gt 0 $,椒噪声;$ Q \lt 0 $,盐噪声;$ Q = 0 $为算数均值滤波
- 中值滤波器:比相同尺寸的线性平滑滤波器引起的模糊更小,在存在单极或双极脉冲噪声(椒噪声 and/or 盐噪声)的情况下,尤其有效
- 最大值降椒噪声,最小值降盐噪声
- 中点滤波器对于随机分布噪声工作得最好(高斯/均匀)
- 高斯噪声和椒盐噪声混合的情况
- 修正的阿尔法均值滤波器,降噪方面更好
- 算术均值和几何均值由于脉冲噪声的存在并没有起到良好的作用
- 使用中值滤波器重复地进行处理$\Longrightarrow$会使得图像变模糊,细节损失
$\Longrightarrow$ 自适应中值滤波器:
- A层确保$Z_{med}(Z_{min} \lt Z_{med} \lt Z_{max})$ 不是脉冲,B层确保$Z_{xy}(Z_{min} \lt Z_{xy} \lt Z_{max})$不是脉冲
- 动态增大窗口
- 不改变“中心灰度级”,减少图像中的失真
- 去除椒盐噪声(脉冲噪声),平滑其他非脉冲噪声,并减少诸如物体边界细化或粗化等失真
- 自适应局部降噪降噪:$\hat{f}(x, y) = g(x, y) \frac{ \sigma^2_{\eta} }{ \sigma^2_L }[g(x, y) - m_L]$
- 参数说明
- 滤波器作用于局部区域$S_{xy}$
- $\sigma^2_{\eta}$ :污染 $f(x, y)$ 以形成 $g(x, y)$ 的噪声的方差
- $m_L$ :$S_{xy}$中像素的局部均值
- $\sigma^2_L$ :$S_{xy}$中像素的局部方差
- 计算结果为局部均值或保留原始像素
- 高局部方差与边缘相关,因此能够保护边缘
- 参数说明
- 逆滤波存在的问题
$$ \hat{F}(u, v) = F(u, v) + \frac{N(u, v)}{H(u, v)} $$- $H(u, v)$ 为零或为非常小的值
- 解决问题的一种方法是限制滤波的频率,使其接近于频谱原点