本文介绍 Divide and Conquer（分而治之） 的一种典型算法，FFT（快速傅里叶变换）。

DFT

DFT：$X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2 \pi k}{N} n}, k = 0, 1, 2, …, N-1$

• for each k: N complex mults, N-1 complex adds
• $e^{-j \frac{2 \pi k}{N} n}$ 预计算并保存在计算机中
• $O(N^2)$ computations for direct DFT $\Longrightarrow$ $O(N log_2 N)$ for FFT

  FFT 算法原理

  　做出如下定义：$W_N = e^{-j \frac{2 \pi}{N}}$，则：$W_N^{kn} = e^{-j \frac{2 \pi k}{N} n}$，具有如下性质：

1. $W_N^{kN} = e^{-j 2 \pi k } = 1$
2. 复共轭对称：$W_N^{k(N-n)} = W_N^{-kn)} = (W_N^{kn})^{*}$
3. 周期性：$W_N^{kn} = W_N^{k(N+n))} = W_N^{(k+N)n}$

　假设 $N = 2^m$，separate $x[n]$ into even and odd-indexed subsequences
　$ X[k] = \sum_{n=0}^{N-1} x[n] W_N^{kn} = \sum_{n \in even} x[n] W_N^{kr} + \sum_{n \in odd} x[n] W_N^{kr} $
　$ X[k] = \sum_{r=0}^{\frac{N}{2}-1} x[2r] W_N^{k 2r} + \sum_{r=0}^{\frac{N}{2}-1} x[2r+1] W_N^{k(2r+1)} $
　　　$ = \sum_{r=0}^{\frac{N}{2}-1} x[2r] (W_N^2)^{kr} + W_N^k \sum_{r=0}^{\frac{N}{2}-1} x[2r+1] (W_N^2)^{kr} $
　But：$W_N^2 = e^{-j \frac{2 \pi}{N} 2} = e^{-j \frac{2 \pi}{\frac{N}{2}}} = W_{\frac{N}{2}}$
　$ X[k] = \sum_{r=0}^{\frac{N}{2}-1} x[2r] W_{\frac{N}{2}}^{kr} + W_N^k \sum_{r=0}^{\frac{N}{2}-1} x[2r+1] W_{\frac{N}{2}}^{kr} $
　　　$ = X_e[k] + W_N^k X_o[k]$
　其中，$X_e[k]$：N/2 DFT of even samples，$X_o[k]$：N/2 DFT of odd samples，$X[k] \Rightarrow$ sum of 2 N/2 point DFTs
　
　举$N=8$作为一个例子，根据上述的思路进行一次二分，如下图：

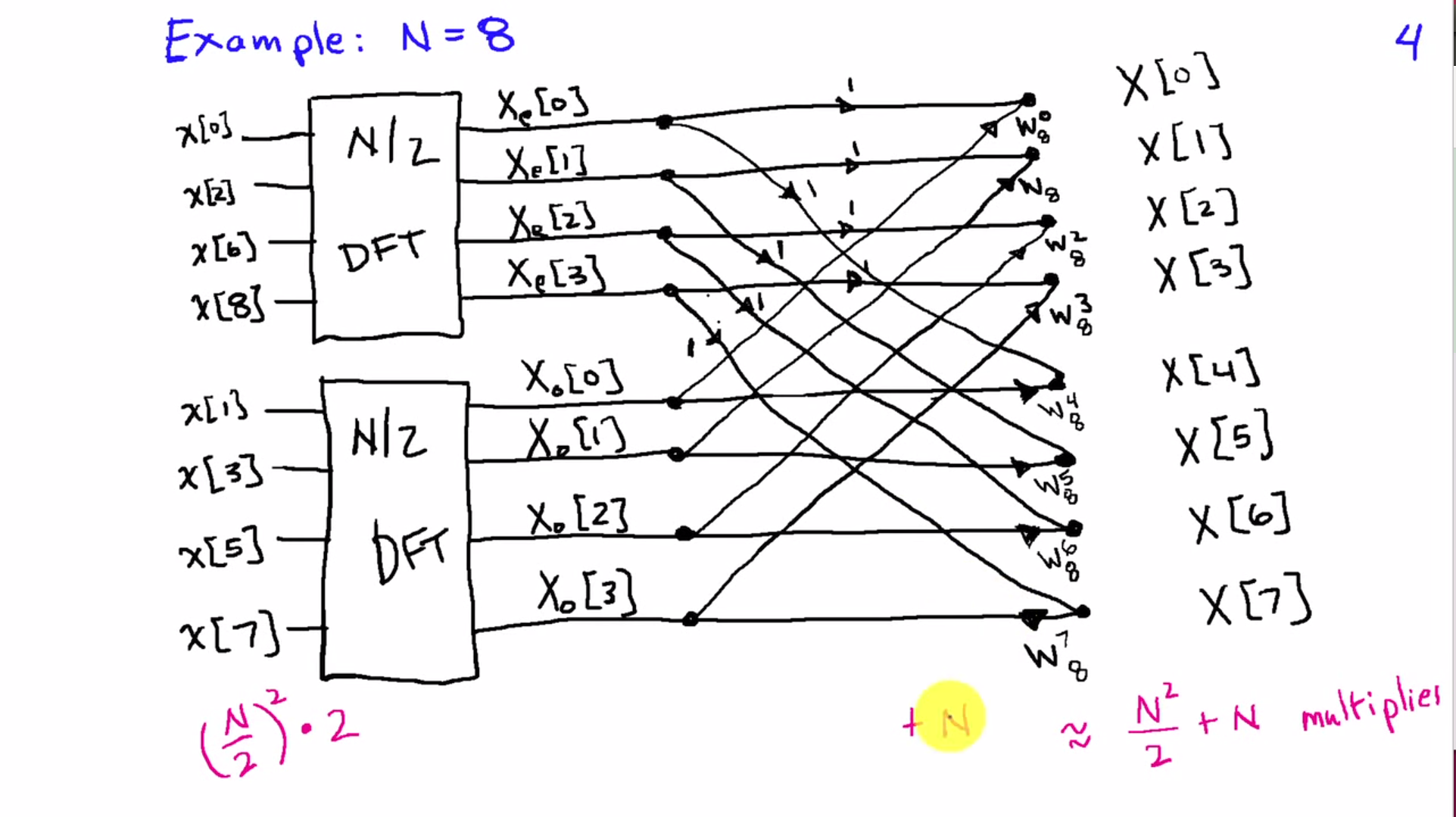
　左边按照普通的 DFT 计算（$O(n^2)$的时间复杂度）得到$x_e[0…3]$和$x_o[0…3]$，需要$(\frac{N}{2})^2·2$ 次乘法；$W_8^{0…7}$ 的预计算需要 $N$ 次乘法；最后的 $X[0…7]$ 的计算每一项都需要一次乘法，总共需要 $N$ 次乘法。故通过一次二分得出的计算复杂度估计为 $\frac{N^2}{2} + N$

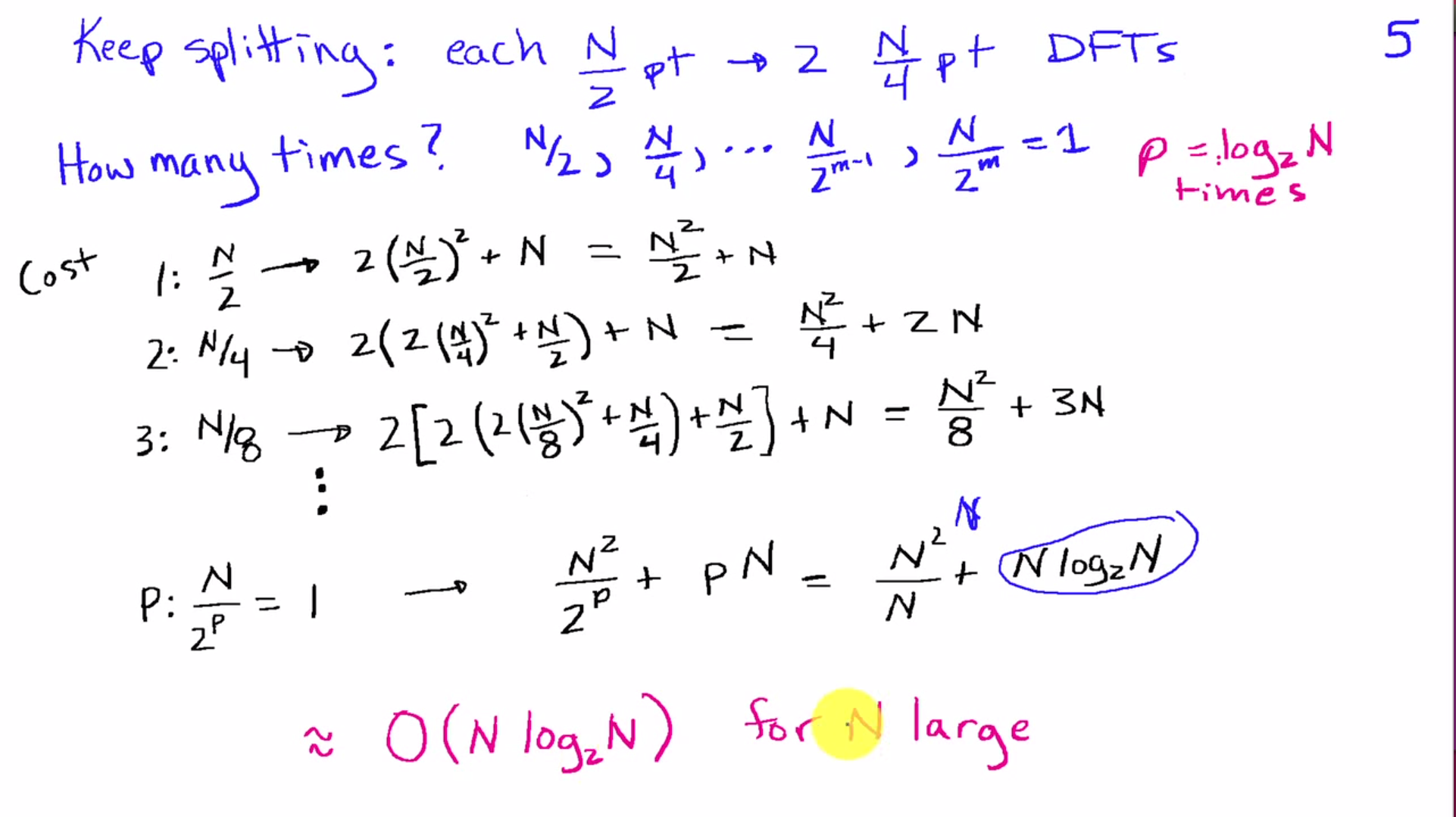
　按照这种思路，继续二分下去（如下图），得到 FFT 算法的最终时间复杂度：$O(N log_2 N)$

FFT算法实现

• 源代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212

  // FFT.cpp #include <stdio.h> #include <stdlib.h> #include <time.h> #include <math.h> #ifndef M_PI #define M_PI 3.14159265358979323846 #endif #define SIZE 1024*16 #define VALUE_MAX 1000 // define a complex structure struct Complex_ { double real; double imagin; }; typedef struct Complex_ Complex; // define complex computation: add/subtract/multiply void Complex_Add(Complex* src1, Complex* src2, Complex* dst){ dst->real = src1->real + src2->real; dst->imagin = src1->imagin + src2->imagin; } void Complex_Sub(Complex* src1, Complex* src2, Complex* dst){ dst->real = src1->real - src2->real; dst->imagin = src1->imagin - src2->imagin; } void Complex_Multiply(Complex* src1, Complex* src2, Complex* dst){ double r1 = 0.0, r2 = 0.0; double i1 = 0.0, i2 = 0.0; r1 = src1->real; i1 = src1->imagin; r2 = src2->real; i2 = src2->imagin; dst->real = r1*r2 - i1*i2; dst->imagin = i1*r2 + r1*i2; } // get W_N^k void getWN(double k, double N, Complex* dst){ double x = 2.0*M_PI*k/N; dst->real = cos(x); dst->imagin = -sin(x); } // input generator void input_generator(double* data, int n){ srand((int)time(0)); for(int i=0; i<SIZE; i++){ data[i] = rand()%VALUE_MAX; printf("%lf\n",data[i]); } } /* * normal DFT algorithm, with O(n^2) complexity */ void DFT(double* src, Complex* dst, int size) { clock_t start, end; start = clock(); // 2 cycle, each with step of 1, size n, so O(n*n) for(int m=0; m<size; m++){ double real = 0.0; double imagin = 0.0; for(int n=0; n<size; n++){ double x = M_PI*2*m*n; real += src[n]*cos(x/size); imagin += src[n]*(-sin(x/size)); } dst[m].imagin = imagin; dst[m].real = real; if(imagin >= 0.0) printf("%lf+%lfj\n", real, imagin); else printf("%lf%lfj\n", real, imagin); } end = clock(); printf("DFT use time :%lf for Datasize of:%d\n",(double)(end-start)/CLOCKS_PER_SEC, size); } void IDFT(Complex* src, Complex* dst, int size) { clock_t start, end; start = clock(); for(int m=0; m<size; m++) { double real = 0.0; double imagin = 0.0; for(int n=0; n<size; n++) { double x = M_PI*2*m*n/size; real += src[n].real*cos(x)-src[n].imagin*sin(x); imagin += src[n].real*sin(x)+src[n].imagin*cos(x); } real /= SIZE; imagin /= SIZE; if(dst != NULL){ dst[m].real = real; dst[m].imagin = imagin; } if(imagin >= 0.0) printf("%lf+%lfj\n", real, imagin); else printf("%lf%lfj\n", real, imagin); } end=clock(); printf("IDFT use time :%lfs for Datasize of:%d\n", (double)(end-start)/CLOCKS_PER_SEC,size); } // define FFT initialization data, remapping int FFT_remap(double* src, int N) { if(N == 1) return 0; double* temp = (double *)malloc(sizeof(double)*N); for(int i=0; i<N; i++) if(i%2==0) temp[i/2] = src[i]; else temp[(N+i)/2] = src[i]; for(int i=0; i<N; i++) src[i] = temp[i]; free(temp); FFT_remap(src, N/2); FFT_remap(src+N/2, N/2); return 1; } void FFT(double* src, Complex* dst, int N){ FFT_remap(src, N); for(int i=0; i<N; i++) printf("%lf\n", src[i]); clock_t start, end; start = clock(); int n = N; int k = 0; // get number of stage int stage = 0; while(n /= 2) { stage++; } n = stage; if(N != (1<<n)) exit(0); Complex* src_complex = (Complex*)malloc(sizeof(Complex)*N); if(src_complex == NULL) exit(0); for(int i=0; i<N; i++){ src_complex[i].real = src[i]; src_complex[i].imagin = 0; } for(int i=0; i<n; i++) { k = 0; for(int j=0; j<N; j++) { if((j/(1<<i))%2 == 1) { Complex WNk; getWN(k, N, &WNk); Complex_Multiply(&src_complex[j], &WNk, &src_complex[j]); k += 1<<(k-i-1); Complex temp; int neighbour = j-(1<<(i)); temp.real = src_complex[neighbour].real; temp.imagin = src_complex[neighbour].imagin; Complex_Add(&temp, &src_complex[j], &src_complex[neighbour]); Complex_Sub(&temp, &src_complex[j], &src_complex[j]); } else k = 0; } } for(int i=0; i<N; i++) { if(src_complex[i].imagin >= 0.0) { printf("%lf+%lfj\n", src_complex[i].real, src_complex[i].imagin); } else printf("%lf%lfj\n", src_complex[i].real, src_complex[i].imagin); } for(int i=0; i<N; i++){ dst[i].imagin = src_complex[i].imagin; dst[i].real = src_complex[i].real; } end = clock(); printf("FFT use time :%lfs for Datasize of:%d\n",(double)(end-start)/CLOCKS_PER_SEC, N); } int main(int argc, char* argv[]) { double input[SIZE]; Complex dst[SIZE]; input_generator(input, SIZE); printf("\n\n"); DFT(input, dst, SIZE); printf("\n\n"); FFT(input, dst, SIZE); return 0; }

　

• 编译构建

  1	$ gcc -o FFT FFT.cpp -lm

　

• 测试结果

  DFT use time :33.963164 for Datasize of:16384
  FFT use time :0.090624s for Datasize of:16384