2017-03-15

算法设计与分析[0004] Depth First Search（深度优先搜索）

　本文主要介绍 DFS 的 C++ 和 C 语言实现，并借助 LeetCode 上的一道题，说说基本的 DFS 在问题求解中的应用。

What’s D(epth)F(irst)S(earch)

　深度优先搜索算法（Depth First Search），是搜索算法的一种。是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点 N 的所有边都己被探寻过，搜索将回溯到发现节点 N 的那条边的起始节点，这一过程一直进行到已发现从源节点可达的所有节点为止。
　如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

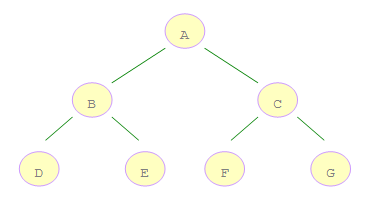
　如上图所示的二叉树，A 是第一个访问的，然后顺序是 B、D，然后是 E。接着再是 C、F、G。

DFS（C++）

C++ 中借助堆栈数据结构来保证这个访问的顺序。由于堆栈是后进先出的顺序，由此可以先将右子树压栈，然后再对左子树压栈，这样一来，左子树结点就存在了栈顶上，因此某结点的左子树能在它的右子树遍历之前被遍历。这样一来，在遍历了根结点后，就开始遍历左子树，最后才是右子树（void depthFirstSearch(Tree root) ）。

// DFS.cpp
#include <stdio.h>
#include <malloc.h>
#include <stack>
 
using namespace std;
 
#define ELEMENT char
#define FORMAT "%c"
#define NODE_NUM 15
 
typedef struct Node {
    ELEMENT data;
    struct Node* left;
    struct Node* right;
}* Tree;
 
/*
 * Binary Tree Constructor
 *  1. construct in preorder
 *  2. '#' means no left child or right child
 */
void binaryTreeConstructor(Tree &root, ELEMENT data[]) {
    static int index = 0;
    if(index >= NODE_NUM) {
        return;
    }
 
    ELEMENT ele = data[index++];
    if(ele == '#') {
        root = NULL;
    }else {
        root = (Node *)malloc(sizeof(Node));
        root->data = ele;
        binaryTreeConstructor(root->left, data);
        binaryTreeConstructor(root->right, data);
    }
}
 
void depthFirstSearch(Tree root) {
    stack<Node *> treeStack;                    // using stack in STL
    treeStack.push(root);
    Node* curNode;
    while(!treeStack.empty()) {
        curNode = treeStack.top();
        treeStack.pop();
        printf(FORMAT, curNode->data);
 
        if(curNode->right) {
            treeStack.push(curNode->right);     // push right child first
        }
        if(curNode->left) {
            treeStack.push(curNode->left);
        }
    }
}
 
int main() {
    ELEMENT data[NODE_NUM] = {'A', 'B', 'D', '#', '#', 'E', '#', '#', 'C', 'F','#', '#', 'G', '#', '#'};
    Tree tree;
    binaryTreeConstructor(tree, data);
 
    printf("Traversal using DFS: ");
    depthFirstSearch(tree);
    printf("\n");
    return 0;
}

　构建运行，结果如下：

1
2
3

gary@xxx:xxx$ g++ DFS.cpp -o DFS
gary@xxx:xxx$ ./DFS
Traversal using DFS: ABDECFG

DFS（C）

C语言 中采取类似的策略，使用的是递归调用这个“堆栈”（void dfs(Node tree[], int vertexIndex, bool visited[])）。

// DFS.c
#include <stdlib.h>
#include <stdio.h>
 
#define NODENUM 7            	// node number
#define ELEMENT char
#define FORMAT "%c "
 
typedef enum {false, true} bool;

// structure for adjacency lists
typedef struct AdjList {
  int vertexIndex; 
  struct AdjList* next;
} AdjList;
  
// Graphic node structure
typedef struct {
  ELEMENT data;			// data area
  struct AdjList* listAdj; 	// pointing to neighbouring node
} Node;
 
int createTree(Node[]);
// return the location of current vertex data in array, -1 if not exit. 
int locate(char, Node[]);
void traverseDFS(Node[]);
void dfs(Node[], int, bool[]);
 
void treeRelease(Node[]);
 
int main(int argc, char* argv[]) {
  Node tree[NODENUM+1];
 
  if(createTree(tree)) {
    printf("DFS result as follow:\n");
    traverseDFS(tree);
    putchar('\n');
 
    treeRelease(tree);
  }
  else {
    printf("Create graphic fail!\n");
  }
 
  return EXIT_SUCCESS;
}
 
/*
 * 1. create a tree by entering all nodes' value and edges of the tree
 * 2. store the tree in an adjacency list
 */
int createTree(Node tree[]) {
  int i,location;
  char c;
 
  printf("Input all nodes's value(should be in [A~Z]||[a~z]):\n");
  for(i=0; i<NODENUM; i++) {
    tree[i].data = getchar();
    if(tree[i].data < 'A' || (tree[i].data > 'Z' && tree[i].data < 'a') || tree[i].data > 'z') {
      printf("Node's value should be in [A~Z]||[a~z]\n");
      exit(EXIT_FAILURE);
    }
  }
  // eliminate '\n'
  getchar();
 
  printf("\nInput the directly connected nodes, given a node:\n");
  for(i = 0; i < NODENUM; i++) {
    putchar(tree[i].data);
    putchar(' ');
    c = getchar();
    tree[i].listAdj = NULL;
    while((location = locate(c, tree)) != -1) {
      AdjList* newAdjVertex = (AdjList *)malloc(sizeof(AdjList));
      newAdjVertex->vertexIndex = location;
      newAdjVertex->next = NULL;
 
      // insert an adjacent node, as the head need to be dealt with separately 
      if(tree[i].listAdj == NULL) {
        tree[i].listAdj = newAdjVertex;
      }
      else {
        AdjList* temp = tree[i].listAdj;
        while(temp->next != NULL) {
          temp = temp->next;
        }
        temp->next = newAdjVertex;
      }
 
      // '\n' will lead to exit
      c = getchar();
    }
  }
 
  return 1;
}
 
// return the index of the given node in the node array, -1 if not exist.
int locate(ELEMENT givenVal, Node tree[]) {
  int location;
  for(location = NODENUM-1; location>=0; location--) {
    if(tree[location].data == givenVal) {
      break;
    }
  }
  return location;
}
 
void traverseDFS(Node tree[]) {
  int i;
  static bool visited[NODENUM];
  for(i=0; i<NODENUM; i++) {
    visited[i] = false;
  }
  // need to traverse all nodes, avoid not-connected graph
  for(i=0; i<NODENUM; i++){
    if(!visited[i]) {
      dfs(tree, i, visited);
    }
  }
}
 
void dfs(Node tree[], int vertexIndex, bool visited[]) {
  AdjList *pAdjList;
 
  printf(FORMAT, tree[vertexIndex].data);
  visited[vertexIndex] = true;
 
  pAdjList = tree[vertexIndex].listAdj;
  while(pAdjList != NULL) {
    vertexIndex = pAdjList->vertexIndex;
    if(!visited[vertexIndex]) {
      dfs(tree, vertexIndex, visited);
    }
    pAdjList = pAdjList->next;
  }
}
 
// reslease the dynamically allocated memory
void treeRelease(Node tree[]) {
  AdjList *p, *temp;
  int i;
  for(i=0; i<NODENUM; i++) {
    p = tree[i].listAdj;
    while(p != NULL){
      temp = p;
      p = p->next;
      free(temp);
    }
  }
}

　构建运行，结果如下：

gary@xxx:xxx$ g++ DFS.c -o DFS
gary@xxx:xxx$ ./DFS
Input all nodes's value(should be in [A~Z]||[a~z]):
ABCDEFG
 
Input the directly connected nodes, given a node:
A BC
B ADE
C AFG
D B
E B
F C
G C
DFS result as follow:
A B D E C F G

112.&113. Path Sum I&II

Description
　Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
　For example:
　Given the below binary tree and sum = 22,
1
2
3
4
5
6
7
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
　即：

给定一个二叉树root和一个和sum，
 
决定这个树是否存在一条从根到叶子的路径使得沿路所有节点的和等于给定的sum。
 
例如：
给定如下二叉树和sum=22，
              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1
返回真，因为这里存在一条根叶路径（5->4->11->2），它的和为22。
 
112&113 都是这样的问题，只不过前者只需要判断是否存在，后者则需要遍历所有节点以得到所有满足条件情况：
　return
　[
   　[5,4,11,2],
   　[5,8,4,5]
　]

解题思路
- 是一个典型的 DFS 遍历的问题，因为需要遍历 root->leaf 这样一类路径，通过递归实现。
- 需要考虑的是在 path 上传递的变量（递归调用过程中传递的参数），问题 112 只需要传递 root->当前节点 的求和（这里通过 Sum 减去当前节点值的方式），如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        // 1. An empty tree
        if(!root) {
            return false;
        }
        // 2. A leaf, check sum
        if(!root->left && !root->right) {
            return (root->val == sum);
        }
        // 3. Not a leaf, recursive to a child node(|| for "exist")
        return hasPathSum(root->left, sum-(root->val)) || hasPathSum(root->right, sum-(root->val));
    }
};

问题 113 除了传递 Sum 外，还需要传递 root->leaf 路径上的节点值。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<vector<int>> pathSet;
        // 1. An empty tree, return empty path Set
        if(root) {
            vector<int> path;
            dfs(root, sum, path, pathSet);
        }
        
        return pathSet;
    }
    
    void dfs(TreeNode* root, int sum, vector<int>& curPath, vector<vector<int>>& pathSet) {
        curPath.push_back(root->val);
        sum -= root->val;
        
        // 2. A leaf reached
        if(!root->left && !root->right) {
            if(sum==0) {
                pathSet.push_back(curPath);
            }
        }
        // 3. Recursive to a child node
        else {
            if(root->left) {
                dfs(root->left, sum, curPath, pathSet);
            }
            if(root->right) {
                dfs(root->right, sum, curPath, pathSet);
            }
        }
        
        // backtracking
        curPath.pop_back();
    }
};

　此外还需要留意 backtracking 部分，因为对于 Sum，是一个形式参数，当递归函数返回时，不影响调用函数中的 Sum，但对于引用参数 curPath 就不一样了，因此，需要在递归函数返回前进行回溯，保证 curPath 始终记录 root->当前节点 路径上的节点值。

本文标题:算法设计与分析[0004] Depth First Search（深度优先搜索）

文章作者:Gary

发布时间:2017-03-15, 14:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/03/15/Algorithms_DFS/