2017-03-22

算法设计与分析[0005] Breadth First Search（广度优先搜索）

　本文主要介绍 BFS 的 C++ 和 C 语言实现，并借助 LeetCode 上的一道题，说说基本的 BFS 在问题求解中的应用。

What’s B(readth)F(irst)S(earch)

　广度优先搜索算法（Breadth First Search），又叫宽度优先搜索，或横向优先搜索。是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

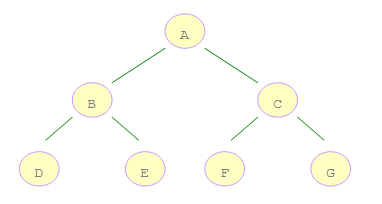
　如上图所示的二叉树，A 节点第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。

BFS（C++）

C++ 中借助队列数据结构来保证这个访问的顺序。由于队列是先进先出的顺序，因此可以先将左子树入队，然后再将右子树入队，这样一来，左子树结点就存在队头，可以先被访问到（void breadthFirstSearch(Tree root) ）。

// BFS.cpp
#include <stdio.h>
#include <malloc.h>
#include <queue>
 
using namespace std;
 
#define ELEMENT char
#define FORMAT "%c"
#define NODE_NUM 15
 
typedef struct Node {
    ELEMENT data;
    struct Node* left;
    struct Node* right;
}* Tree;
 
/*
 * Binary Tree Constructor
 *  1. construct in preorder
 *  2. '#' means no left child or right child
 */
void binaryTreeConstructor(Tree &root, ELEMENT data[]) {
    static int index = 0;
    if(index >= NODE_NUM) {
        return;
    }
 
    ELEMENT ele = data[index++];
    if(ele == '#') {
        root = NULL;
    }else {
        root = (Node *)malloc(sizeof(Node));
        root->data = ele;
        binaryTreeConstructor(root->left, data);
        binaryTreeConstructor(root->right, data);
    }
}
 
void breadthFirstSearch(Tree root) {
    queue<Node *> treeQueue;			// using queue in STL
    treeQueue.push(root);
    Node* curNode;
    while(!treeQueue.empty()) {
        curNode = treeQueue.front();
        treeQueue.pop();
        printf(FORMAT, curNode->data);
 
        if(curNode->left) {
            treeQueue.push(curNode->left);	// push left child first
        }
        if(curNode->right) {
            treeQueue.push(curNode->right);
        }
    }
}
 
int main() {
    ELEMENT data[NODE_NUM] = {'A', 'B', 'D', '#', '#', 'E', '#', '#', 'C', 'F','#', '#', 'G', '#', '#'};
    Tree tree;
    binaryTreeConstructor(tree, data);
 
    printf("Traversal using BFS: ");
    breadthFirstSearch(tree);
    printf("\n");
    return 0;
}

　构建运行，结果如下：

1
2
3

gary@xxx:xxx$ g++ BFS.cpp -o BFS
gary@xxx:xxx$ ./BFS 
Traversal using BFS: ABCDEFG

BFS（C）

C语言 中采取类似的策略，不过需要手动实现一个队列功能（void bfs(Node tree[], int vertexIndex, bool visited[])）。

// BFS.c
#include <stdlib.h>
#include <stdio.h>
 
#define NODENUM 7            	// node number
#define ELEMENT char
#define FORMAT "%c "
 
typedef enum {false, true} bool;
 
// structure for adjacency lists
typedef struct AdjList {
  int vertexIndex;
  struct AdjList* next;
} AdjList;
 
// Graphic node structure
typedef struct {
  ELEMENT data;			// data area
  struct AdjList* listAdj; 	// pointing to neighbouring node
} Node;
 
int createTree(Node[]);
// return the location of current vertex data in array, -1 if not exit. 
int locate(char, Node[]);
void traverseBFS(Node[]);
void bfs(Node[], int, bool[]);
 
void treeRelease(Node[]);
 
int main(int argc, char* argv[]) {
  Node tree[NODENUM+1];
 
  if(createTree(tree)) {
    printf("BFS result as follow:\n");
    traverseBFS(tree);
    putchar('\n');
 
    treeRelease(tree);
  }
  else {
    printf("Create graphic fail!\n");
  }
 
  return EXIT_SUCCESS;
}
 
/*
 * 1. create a tree by entering all nodes' value and edges of the tree
 * 2. store the tree in an adjacency list
 */
int createTree(Node tree[]) {
  int i,location;
  char c;
 
  printf("Input all nodes's value(should be in [A~Z]||[a~z]):\n");
  for(i=0; i<NODENUM; i++) {
    tree[i].data = getchar();
    if(tree[i].data < 'A' || (tree[i].data > 'Z' && tree[i].data < 'a') || tree[i].data > 'z') {
      printf("Node's value should be in [A~Z]||[a~z]\n");
      exit(EXIT_FAILURE);
    }
  }
  // eliminate '\n'
  getchar();
 
  printf("\nInput the directly connected nodes, given a node:\n");
  for(i = 0; i < NODENUM; i++) {
    putchar(tree[i].data);
    putchar(' ');
    c = getchar();
    tree[i].listAdj = NULL;
    while((location = locate(c, tree)) != -1) {
      AdjList* newAdjVertex = (AdjList *)malloc(sizeof(AdjList));
      newAdjVertex->vertexIndex = location;
      newAdjVertex->next = NULL;
 
      // insert an adjacent node, as the head need to be dealt with separately 
      if(tree[i].listAdj == NULL) {
        tree[i].listAdj = newAdjVertex;
      }
      else {
        AdjList* temp = tree[i].listAdj;
        while(temp->next != NULL) {
          temp = temp->next;
        }
        temp->next = newAdjVertex;
      }
 
      // '\n' will lead to exit
      c = getchar();
    }
  }
 
  return 1;
}
 
// return the index of the given node in the node array, -1 if not exist.
int locate(ELEMENT givenVal, Node tree[]) {
  int location;
  for(location = NODENUM-1; location>=0; location--) {
    if(tree[location].data == givenVal) {
      break;
    }
  }
  return location;
}
 
void traverseBFS(Node tree[]) {
  int i;
  static bool visited[NODENUM];
  for(i=0; i<NODENUM; i++) {
    visited[i] = false;
  }
  // need to traverse all nodes, avoid not-connected graph
  for(i=0; i<NODENUM; i++){
    if(!visited[i]) {
      bfs(tree, i, visited);
    }
  }
}
 
void bfs(Node tree[], int vertexIndex, bool visited[]) {
  /*
	 * 采用队列，访问一个节点并让其入队，然后按照同样的方法访问其兄弟节点，访问完毕
	 * 然后再从队列里按顺序再拉出一个节点来，继续访问
	 */
  int treeQueue[NODENUM];
  int popIdx=0, pushIdx=0;
  AdjList *pAdjList;

  printf(FORMAT, tree[vertexIndex].data);
  visited[vertexIndex] = true;
  treeQueue[0] = vertexIndex;			// insert the first node
 
  while(popIdx <= pushIdx) {
    vertexIndex = treeQueue[popIdx++];		// pop one by one in the queue
    pAdjList = tree[vertexIndex].listAdj;
    while(pAdjList != NULL) {
      vertexIndex = pAdjList->vertexIndex;
      if(!visited[vertexIndex]) {
        printf(FORMAT, tree[vertexIndex].data);
        visited[vertexIndex] = true;
        treeQueue[++pushIdx] = vertexIndex;	// push adjacent nodes into the queue 
      }
      pAdjList = pAdjList->next;
    }
  }
}
 
// reslease the dynamically allocated memory
void treeRelease(Node tree[]) {
  AdjList *p, *temp;
  int i;
  for(i=0; i<NODENUM; i++) {
    p = tree[i].listAdj;
    while(p != NULL){
      temp = p;
      p = p->next;
      free(temp);
    }
  }
}

　构建运行，结果如下：

gary@xxx:xxx$ g++ BFS.c -o BFS
gary@xxx:xxx$ ./BFS
Input all nodes's value(should be in [A~Z]||[a~z]):
ABCDEFG
 
Input the directly connected nodes, given a node:
A BC
B ADE
C AFG
D B
E B
F C
G C
BFS result as follow:
A B C D E F G

102&107. Binary Tree Level Order Traversal I&II

Description
　Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
　For example:
　Given binary tree [3,9,20,null,null,15,7],
1
2
3
4
5
3
/ \
9 20
/ \
15 7

　return its level order traversal as:

[
   [3],
   [9,20],
   [15,7]
]

　即：

给定一个二叉树，返回按层级顺序遍历的每个节点的值。
 
从左到右，逐层遍历。
 
例如：
给定一个二叉树 {3,9,20,#,#,15,7}，
    3
   / \
  9  20
    /  \
   15   7
返回它的层级顺序遍历结果为：
[
  [3],
  [9,20],
  [15,7]
]
102&107 都是这样的问题，只不过前者返回从上至下每一层的所有节点，后者则按照从下到上的顺序。

解题思路
- 是一个典型的 BFS 遍历的问题，因为 BFS 遍历的过程就是一个按层由上至下访问的过程；问题的难点在于，如何区分哪些节点属于哪一层，然后，按照遍历顺序（已经是满足要求的从左到右的顺序），将节点的值插入到每一层对应的向量里面
- 一开始想到的方式是，BFS 遍历通过队列 queue 实现，基本的 BFS 遍历队列维护的只有节点，想要知道每个节点对应的深度，可以维护一个既包含节点又包含节点深度的队列，可以考虑使用 map 字典。

Solution & Analysis

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(!root) {
            return result;
        }
         
        // pair's int for recording depth
        queue<pair<int, TreeNode*>> treeQueue;
        treeQueue.push(make_pair(0, root));
        
        while(!treeQueue.empty()) {
            int curDepth = treeQueue.front().first;
            TreeNode* curNode = treeQueue.front().second;
            treeQueue.pop();
            
            while(result.size() < curDepth+1) {
                result.push_back(vector<int>());
            }
            result[curDepth].push_back(curNode->val);
            
            if(curNode->left) {
                treeQueue.push(make_pair(curDepth+1, curNode->left));
            }
            
            if(curNode->right) {
                treeQueue.push(make_pair(curDepth+1, curNode->right));
            }
        }
        
        return result;
    }
};

　另外需要注意的是 Line: 27-29。一开始我们并不知道这个树有多少层，即 result 结果集的大小，可以利用 vector 自带的动态增长功能灵活检测。
　Accepted，不过耗时：6ms，感觉挺长的…

问题 107 只需要将上述得到的结果集反转一下就可以了，可以直接使用 <algorithm> 库中的 reverse 函数直接调用（如下），不过耗时较大。
1
reverse(result.begin(), result.end());

　使用自己实现的反转函数（如下）效率更高，提交信息号称快了 3ms。

private:
    void orderReverse(vector<vector<int>>& result) {
        int depth;
        vector<int> tmp;
        for(depth=0; depth<result.size()/2; depth++) {
            tmp = result[result.size()-1 - depth];
            result[result.size()-1 - depth] = result[depth];
            result[depth] = tmp;
        }
    }

其他思路的实现
　采用递归实现的 DFS 同样能获取树节点的分层信息。在 DFS 的过程中可以直接记录一下当前递归到第几层，就可能找到当前节点对应着哪一行向量；为了满足在同一层中，所有节点按照从左到右的顺序排列，我们需要让遍历节点的顺序也同样满足先到左边子树的节点，再到右边子树的节点，可以通过先递归处理左子树，再处理右子树来实现。
　此外，与上面解答类似的，由于我们一开始并不知道整个子树的层数，所以需要根据当前的层数去动态结果集中每层节点对应的向量数量。
　代码实现起来比较简单，不过，由于频繁的递归调用，运行时间较长，耗时：9ms

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    void dfs(TreeNode* root, int depth, vector<vector<int>>& result) {
        if (!root) {
            return;
        }
        
        // dynamically increase the size of result
        if (result.size() <= depth){
            result.push_back(vector<int>());
        }
        // put current node's value into corresponding depth index
        result[depth].push_back(root->val);
        
        // recursive to child nodes, first left child, then right
        dfs(root->left, depth+1, result);
        dfs(root->right, depth+1, result);
        
        return;
    }
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        dfs(root, 0, result);
        return result;
    }
};

　下面这一种实现，思路则更加直接：假如每次循环都把上一层的所有节点的左右子树（假如存在）遍历一遍，则会把当前层中的所有节点也遍历一遍；遍历是从根节点出发的，按照这一思路进行迭代，每次循环中将当前循环遍历的当前层所有节点更新成上一层节点；先左子树后右子树以及从0开始遍历上一层的所有节点信息可以保证每一层的节点符合从左往右的顺序。
　这种方式，感觉每个节点都需要遍历两次（一次通过上一层节点左右子树的方式；一次为了遍历下一层节点所作的遍历），所以时间也比较长，耗时：6ms

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(!root) {
            return result;
        }
        
        // record last-layer nodes
        vector<TreeNode*> lastDepth;
        lastDepth.push_back(root);
        
        while(lastDepth.size() > 0) {
            vector<int> tmp;
            vector<TreeNode*> curDepth;
            
            for(int i=0; i<lastDepth.size(); i++) {
                TreeNode* curNode = lastDepth[i];
                tmp.push_back(curNode->val);
                
                if(curNode->left) {
                    curDepth.push_back(curNode->left);
                }
                 if(curNode->right) {
                    curDepth.push_back(curNode->right);
                }
                
            }
            
            if(tmp.size() > 0) {
                result.push_back(tmp);
            }
            
            lastDepth = curDepth;
        }
        
        return result;
    }
};

　最后一种方法，利用这样一种特点：每一层所有节点的左右子树遍历完，则下一层的所有所有节点也被遍历一遍。使用队列这种数据结构实现 BFS，通过向队列中插入额外分割符作为实现层与层之间节点的区分，问题变成何时能够插入这样一个分隔符？这就用到上面的特点，即，当我从队列中取出一个分隔符时，说明上一层的所有节点已经从队列中取出，而且根据上一层所有节点遍历到的所有下一层的节点已经放入队列，因此，此时就需要插入一个分隔符。
　这种方法与普通的 BFS 遍历过程几乎一样，每个节点也只是遍历一遍（额外的分隔符其实并不多吧…），耗时最少：3ms

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
  vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int> > result;
    result.clear();
    if(root == NULL) {
      return result;
    }
    queue<TreeNode*> S;
    S.push(root);
    S.push(NULL);
    
    vector<int> tmp;
    while(!S.empty()){
      // travesal current level
      TreeNode* curNode = S.front();
      S.pop();
      if(curNode != NULL) {
        tmp.push_back(curNode->val);
        if(curNode->left) {
          S.push(curNode->left);
        }
        if(curNode->right) {
          S.push(curNode->right);
        }
      }else {
        if(!tmp.empty()) {	
          S.push(NULL);
          result.push_back(tmp);
          tmp.clear();
        }
      }
    }
    
        return result;
    }
};

本文标题:算法设计与分析[0005] Breadth First Search（广度优先搜索）

文章作者:Gary

发布时间:2017-03-22, 14:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/03/22/Algorithms_BFS/