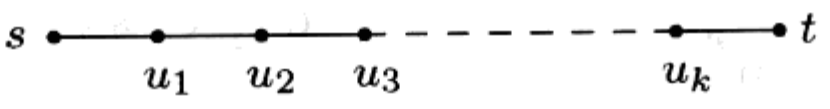算法设计与分析[0006] Some Shortest-path Algorithms（最短路径算法）

编程珠玑Algorithm

　本文介绍几种常见的最短路径算法：

  • Breadth-first Search 无权最短路径算法；
  • Dijkstra 带权（非负权）图的单源最短路算法；
  • Bellman-Ford 带权（可负权）图的单源最短路算法；
  • Floyd-Warshall 带权（可负权）图的全源最短路算法，
    　包括它们各自的使用条件&范围，算法原理介绍以及代码实现。

Breadth-first Search 无权最短路径算法

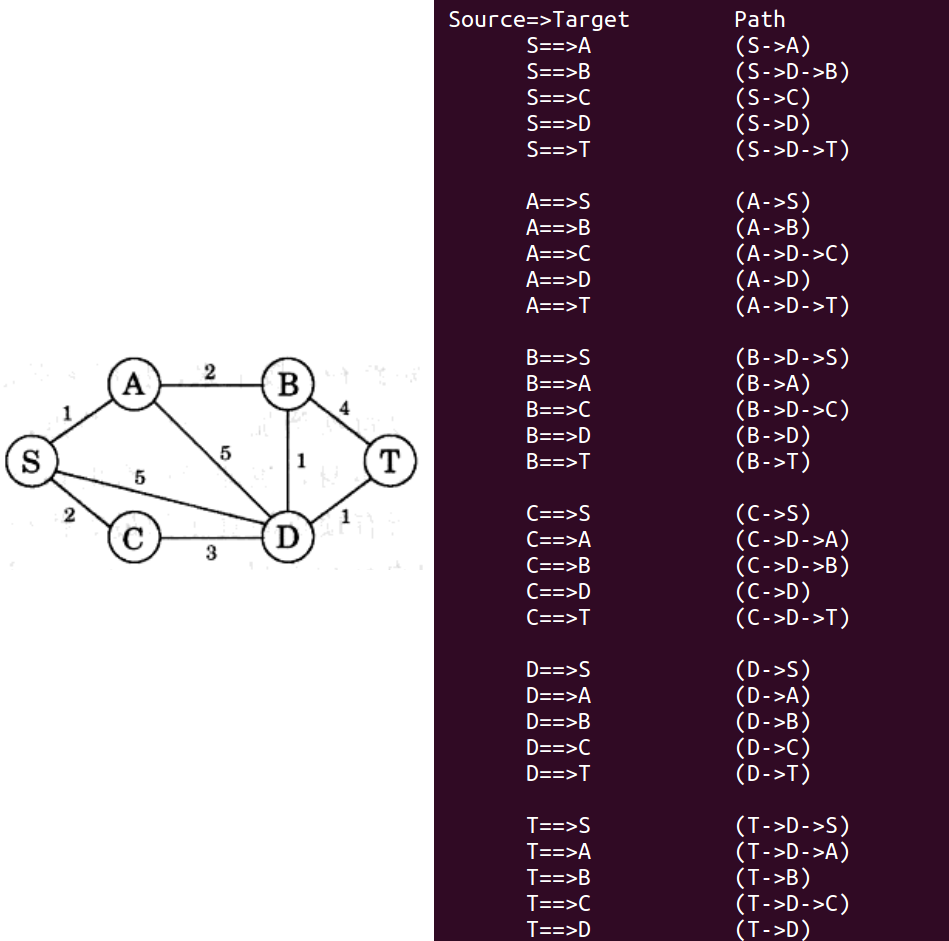
  • BFS 适合边的权值均是 1（无权图）的最短路径问题，因为，假设 S 为起始点，BFS 每次都会先发现距离 S 为 k 的所有顶点，然后才会发现距离 S 为 k+1 的所有顶点。

    ① 对于外面的while循环，会执行|V|次，因为每个顶点入队出队一次。
    ② dist(v)==∞ 说明节点 v 还没被访问，将其放入队列并更新dist值。
    ③ 里面的for循环一共会执行|E|次，即变长，所以该算法时间复杂度为O(|V|+|E|)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
#include <queue>
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
  char data;
  adjVertexNode* list;
  int dist;
  // How to restore a shortest path: recording the pre-visit VertexNode in the path
  VertexNode* preVertexNode;
};
 
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
 
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << " ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
void BFS(Graph& g, VertexNode& Source) {
  queue<VertexNode*> vertexQueue;
  int i;
  for(i=0; i<g.vertexNum; i++) {
    g.VertexNodes[i].dist = INT_MAX;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  Source.dist = 0;
  vertexQueue.push(&Source);
  while (!vertexQueue.empty()) {
    VertexNode* v = vertexQueue.front();
    vertexQueue.pop();
    adjVertexNode* head = v->list;
    while (head != NULL) {
      if (g.VertexNodes[head->adjVertexIdx].dist == INT_MAX) {
        g.VertexNodes[head->adjVertexIdx].dist = v->dist + 1;
        g.VertexNodes[head->adjVertexIdx].preVertexNode = v;
        vertexQueue.push(&g.VertexNodes[head->adjVertexIdx]);
      }
      head = head->next;
    }
  }
}
 
// backtracking for the path
void PrintPath(Graph& g, VertexNode* target) {
  if (target->preVertexNode != NULL) {
    PrintPath(g, target->preVertexNode);
    cout << "->";
  }
  cout << target->data;
}
 
int main(int argc, const char** argv) {
  freopen("BFS.txt", "r", stdin);
  cout << sizeof(VertexNode) << sizeof(adjVertexNode*) << endl;
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  cout << endl;
  cout << "  Source=>Target\tPath" << endl;
  for(int from=0; from<g.vertexNum; from++) {
    BFS(g, g.VertexNodes[from]);
    for(int to=0; to<g.vertexNum; to++) {
      if(from == to) {
        continue;
      }
      cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data << " \t\t(";
      PrintPath(g, &g.VertexNodes[to]);
      cout << ")" << endl;
    }
    cout << endl;
  }
   
  DeleteGraph(g);
  return 0;
}
  • 忽略边的权值，该图对应的输入文件 BFS.txt 如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6 18
S A B C D T
0 1
0 3
0 4
1 0
1 2 
1 4
2 1
2 4
2 5
3 0
3 4
4 0
4 1
4 2
4 3
4 5
5 2
5 4
  • 通过g++进行构建
1
2
// -m32 option for 32-bit execution
g++ [-m32] BFS.cpp -o BFS

更多关于BFS算法的实现，可以点击阅读

Dijkstra 算法

References:

  • Dijkstra 算法推导
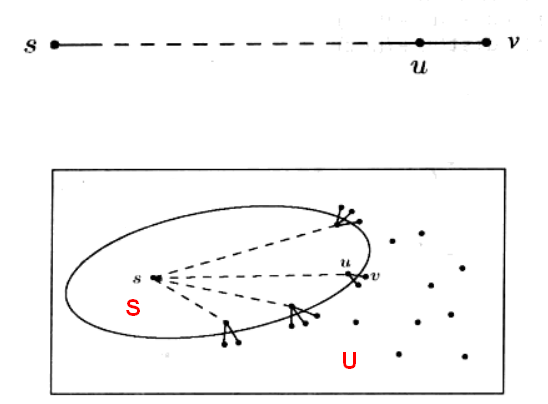
    • 已知区域S 是包含 s 的某个顶点子集。
    • 关于当前最短路径有很多单边扩展路径，其中 u→v 是最短的一条。
    • 上图中，s 到 v 的最短路径即为这样一条路径：基于一条已知的最短路径中的某条边（如上图s→u）的扩展路径。
      • 推导条件：假设无负权，u 一定比 v 距离 s 更近，这意味着 u 在已知区域 S 中，否则将与 v 是 S 之外且与 s 距离最近的顶点 这一假设相矛盾。
    • 检查当前已知最短路径集合 S 的所有单边扩展路径，找到这些扩展路径中的最短路径，该路径的另一个端点即为加入 S 的下一个顶点。
    • 提高算法的执行效率：基于这样一个事实，在算法的任意迭代步骤中，仅有的新扩展路径是那些连接最近加入到 S 中的顶点的路径，其它所有路径的长度之前已经计算过，无需重新计算。
  • Dijkstra 算法思想 ：
    • 左图：① dist(v)：指向 v 的当前最短单边扩展路径的长度（对于与 S 不相邻的顶点，取值为 ∞）；② 每次 while 循环迭代的末尾，（1）存在一个值 d，使得从 s 到 S 中所有顶点的距离 ≤d。同时 s 到 S 外的所有顶点的距离≥d；（2）对于每个顶点 v，dist(v) 表示一条从 s 到 v 的最短路径的长度，该路径经过的顶点均在 S 中（如果不存在这样的路径，dist 为 ∞）。
    • 右图：设 G=(V，E) 是一个带权有向图（无向可以转化为双向有向），把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时 S 中只有一个源点，以后每求得一条最短路径 , 就将其加入到集合 S 中，直到全部顶点都加入到 S 中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中，总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。此外，每个顶点对应一个距离， S 中的顶点的距离就是从 v 到此顶点的最短路径长度， U 中的顶点的距离，是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。
  • Dijkstra 算法具体步骤
    （1）初始时，S只包含源点，即S＝{v}，v的距离dist[v]为0。U包含除v外的其他顶点，U中顶点u距离dis[u]为边上的权值（若v与u有边）或 ∞（若u不是v的出边邻接点即没有边 <v→u>）。
    （2）从U中选取一个距离 v 最小的顶点 k，把 k，加入 S 中（该选定的距离（dist[k]）就是 v 到 k 的最短路径长度）。
    （3）以 k 为新考虑的中间点，修改 U 中各顶点的距离（松弛操作）：若从源点v到顶点u（u∈ U）的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值等于顶点k的距离加上边上的权（即如果 dist[k]+w[k,u]<dist[u]，那么把dist[u]更新成更短的距离 dist[k]+w[k,u]）。
    （4）重复步骤（2）和（3）直到所有顶点都包含在 S 中(要循环n-1次)。
  • 基于数组实现的 Dijkstra 算法（void Dijkstra(Graph& g, VertexNode& Source) 函数）
    • 总共需要循环 |V| 次（步骤（4）），实现将所有节点添加进已知区域 S。
    • 每次循环，需要选取一个距离最小的顶点（步骤（2）），需要对所有节点进行遍历（$O(|V|)$）。
    • 在循环执行的过程中，该循环为了更新距离（步骤（3）），需要访问每条边一次（有向图的情况）或两次（无向图的情况），从而花费了 $O(|E|)$ 的时间。
    • 该算法的整体运行时间为：$O(|V|^2)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  // weight: length on edges
  int weight;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
  char data;
  adjVertexNode* list;
  int dist;
  // How to restore a shortest path: recording the pre-visit VertexNode in the path
  VertexNode* preVertexNode;
};
  
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
  
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
void Dijkstra(Graph& g, VertexNode& Source) {
  bool visited[g.vertexNum];
  for(int i=0; i<g.vertexNum; i++) {
    g.VertexNodes[i].dist = INT_MAX;
    g.VertexNodes[i].preVertexNode = NULL;
    visited[i] = false;
  }
 
  Source.dist = 0;
  for (int vertexNuminS = 0; vertexNuminS < g.vertexNum; vertexNuminS++) {
    // Pick the node not in S with smallest dist
    int minDist = INT_MAX;
    int pickIdx = -1;
    for(int i=0; i<g.vertexNum; i++) {
      if(!visited[i] && g.VertexNodes[i].dist<minDist) {
        minDist = g.VertexNodes[i].dist;
        pickIdx = i;
      }
    }
    // other nodes are unreachable
    if(pickIdx == -1) {
      break;
    }

    visited[pickIdx] = true;
    VertexNode* v = &g.VertexNodes[pickIdx];

    // update the current new extended path and the predecessor vertex
    adjVertexNode* head = v->list;
    while (head != NULL) {
      // visited to avoid repeatedly enqueue
      if(!visited[head->adjVertexIdx] && g.VertexNodes[head->adjVertexIdx].dist 
        > (v->dist + head->weight)) {
        g.VertexNodes[head->adjVertexIdx].dist = v->dist + head->weight;
        g.VertexNodes[head->adjVertexIdx].preVertexNode = v;
      }
      head = head->next;
    }
  }
}
 
// backtracking for the path
void PrintPath(Graph& g, VertexNode* target) {
  if (target->preVertexNode != NULL) {
    PrintPath(g, target->preVertexNode);
    cout << "->";
  }
  cout << target->data;
}
 
int main(int argc, const char** argv) {
  freopen("Dijkstra.txt", "r", stdin);
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  cout << endl;
  cout << "  Source=>Target\tShortest Distance\tPath" << endl;
  for(int from=0; from<g.vertexNum; from++) {
    Dijkstra(g, g.VertexNodes[from]);
    for(int to=0; to<g.vertexNum; to++) {
      if(from == to) {
        continue;
      }
      cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data 
        << "\t\t\t";
      if(g.VertexNodes[to].dist == INT_MAX) {
        cout << "INF";
      }else {
        cout << g.VertexNodes[to].dist;
      }
      cout << " \t\t(";
      PrintPath(g, &g.VertexNodes[to]);
      cout << ")" << endl;
    }
    cout << endl;
  }
   
  DeleteGraph(g);
  return 0;
}
  • 基于 std::priority_queue 实现的 Dijkstra 算法（void Dijkstra(Graph& g, VertexNode& Source) 函数）
    • 由于使用了指针类型（VertexNode*）的优先级队列，需要声明额外的比较方法 struct cmp，重载其 operator()，并按以下方式声明：priority_queue<VertexNode*, vector<VertexNode*>, cmp> vertexQueue;，而不能通过直接重载优先级队列元素类型的比较函数 operator<。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
#include <queue>
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  int weight;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
  char data;
  adjVertexNode* list;
  int dist;
  // How to restore a shortest path: recording the pre-visit VertexNode in the path
  VertexNode* preVertexNode;

  /*
	bool operator< (VertexNode* a, VertexNode* b) {
		return a->dist > b->dist;
	};*/
};
 
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
 
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
/* compare struct for priority queue
 * In order to achieve the minimum heap(in ascending order)
 *   reload operator<, redefine the priority to smaller one
 */
struct cmp {
  bool operator() (VertexNode* a, VertexNode* b) {
    return a->dist > b->dist;
  };
};
 
void Dijkstra(Graph& g, VertexNode& Source) {
  priority_queue<VertexNode*, vector<VertexNode*>, cmp> vertexQueue;
  bool visited[g.vertexNum];
  for(int i=0; i<g.vertexNum; i++) {
    g.VertexNodes[i].dist = INT_MAX;
    g.VertexNodes[i].preVertexNode = NULL;
    visited[i] = false;
  }
 
  Source.dist = 0;
  vertexQueue.push(&Source);
 
  while(!vertexQueue.empty()) {
    VertexNode* v = vertexQueue.top();
    // cout << "pop: " << v->data << " ";
    vertexQueue.pop();
 
    int vertexIdx = v - g.VertexNodes;
    if(visited[vertexIdx]) {
      continue;
    }
    visited[vertexIdx] = true;
 
    adjVertexNode* head = v->list;
    // cout << "push: ";
    // relax operation: update the estimated distance for all adjacent vertex 
    while (head != NULL) {
      /*
			 * A node with different dist will be pushed repeatedly for smallest one
			 *  use visited(visited[vertexIdx]) flag to avoid not-smallest visit
			 * A node in known-region should't be repeatedly updated 
			 *	use visited[head->adjVertexIdx]
			 */ 
      if(!visited[head->adjVertexIdx] && g.VertexNodes[head->adjVertexIdx].dist 
        > (v->dist + head->weight)) {
        g.VertexNodes[head->adjVertexIdx].dist = v->dist + head->weight;
        g.VertexNodes[head->adjVertexIdx].preVertexNode = v;
        vertexQueue.push(&g.VertexNodes[head->adjVertexIdx]);
        // cout << g.VertexNodes[head->adjVertexIdx].data << " ";
      }
      head = head->next;
    }
    // cout << endl;
  }
}
 
// backtracking for the path
void PrintPath(Graph& g, VertexNode* target) {
  if (target->preVertexNode != NULL) {
    PrintPath(g, target->preVertexNode);
    cout << "->";
  }
  cout << target->data;
}
 
int main(int argc, const char** argv) {
  freopen("Dijkstra.txt", "r", stdin);
  //freopen("BellmanFord.txt", "r", stdin);
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  cout << endl;
  cout << "  Source=>Target\tShortest Distance\tPath" << endl;
  for(int from=0; from<g.vertexNum; from++) {
    Dijkstra(g, g.VertexNodes[from]);
    for(int to=0; to<g.vertexNum; to++) {
      if(from == to) {
        continue;
      }
      cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data 
        << "\t\t\t";
      if(g.VertexNodes[to].dist == INT_MAX) {
        cout << "INF";
      }else {
        cout << g.VertexNodes[to].dist;
      }
      cout << " \t\t(";
      PrintPath(g, &g.VertexNodes[to]);
      cout << ")" << endl;
    }
    cout << endl;
  }
   
  DeleteGraph(g);
  return 0;
}
  • 注意：
    • 基于优先级队列实现的 Dijkstra 算法，为了保证每次迭代均能够获取未知区域中距离源点最近的顶点，存在将一个节点重复入队的情况。当该节点被加入到已知区域时，这种重复入队保证其距离为最短距离；此后，队列中存在该节点的残留节点（距离不是最短距离）的可能，需要滤除这些残留节点。
    • Dijkstra 算法 中，已知区域内的顶点距离确定是最短距离，因此不应由于新节点的加入而发生更新。对于正权图，不会对已知区域内的节点进行松弛操作；对于负权图，则可能发生，因此需要对松弛操作节点范围进行限制。
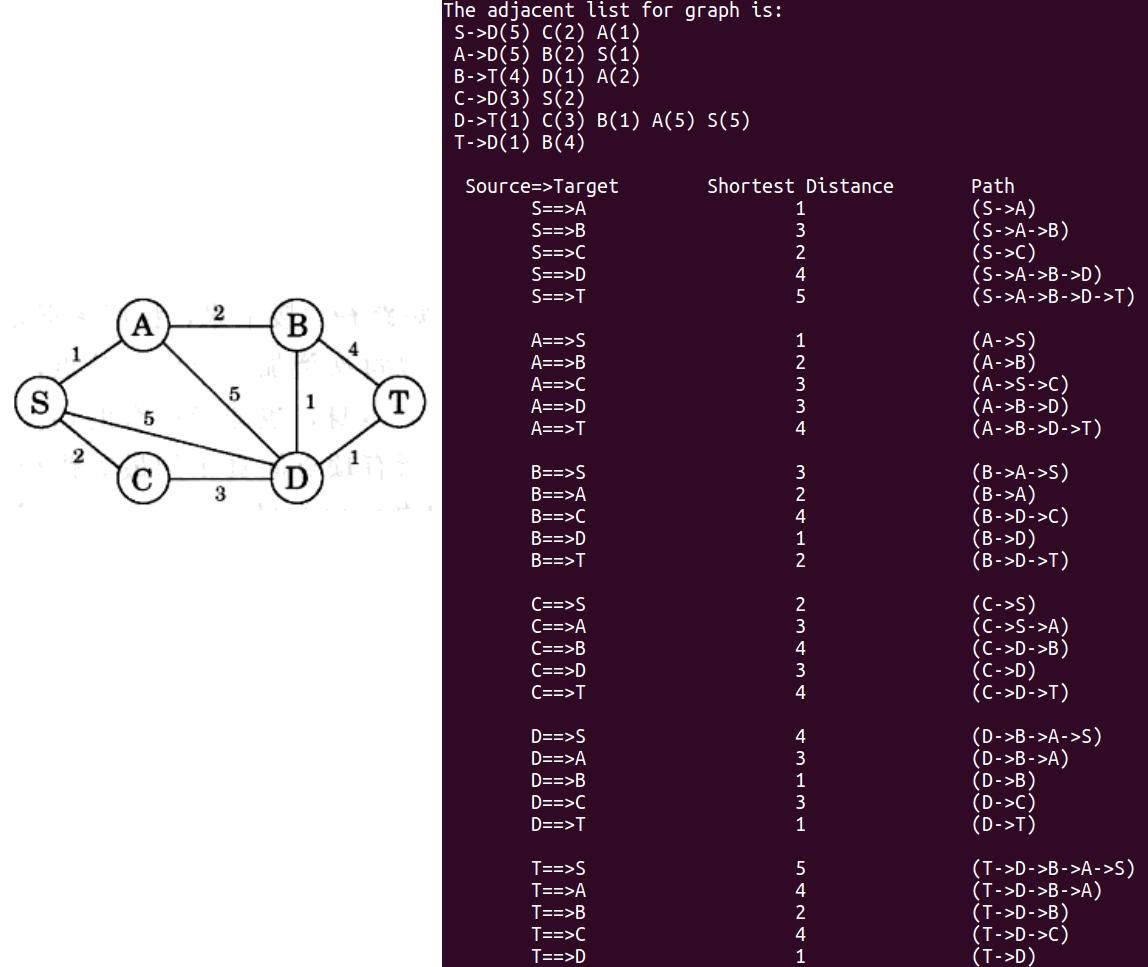
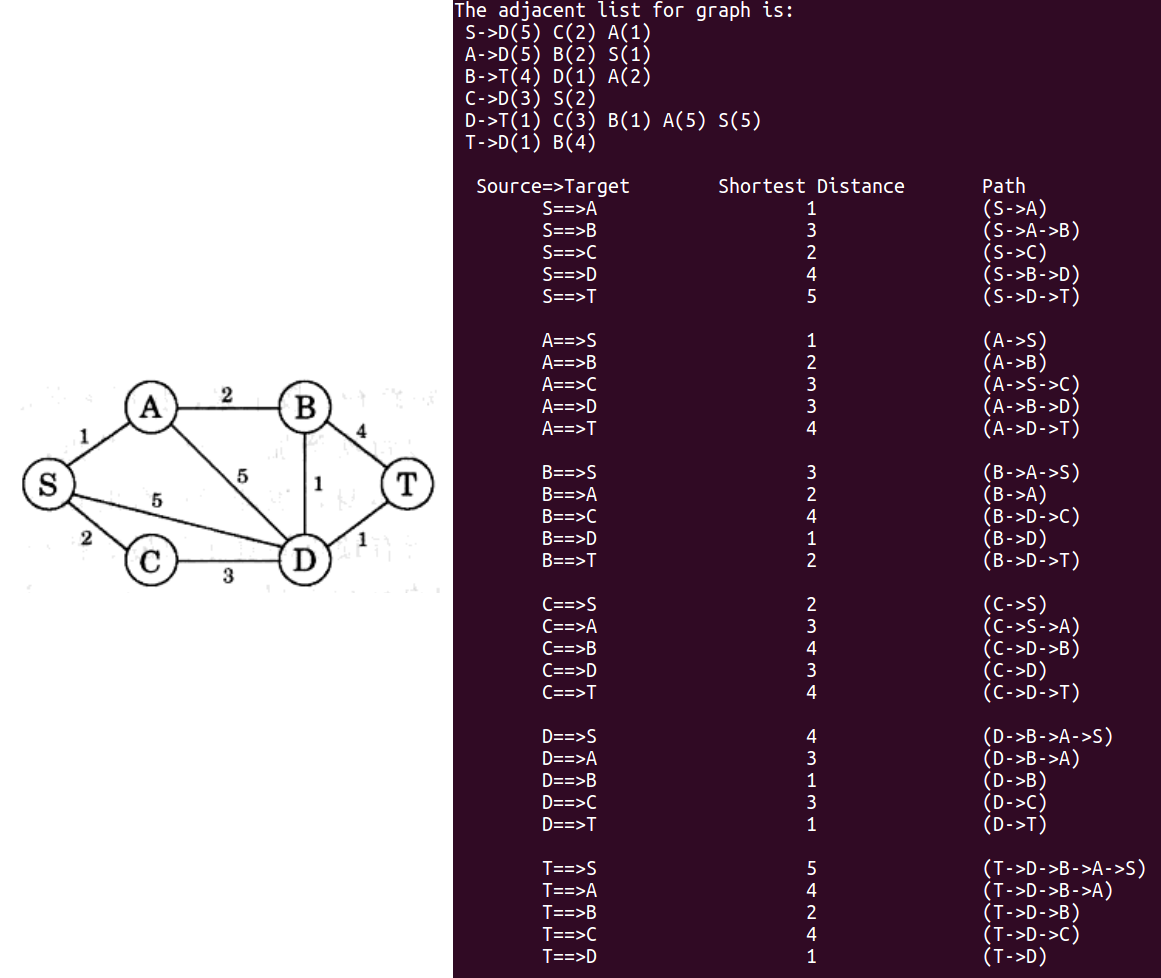
  • 上图对应的输入文件 Dijkstra.txt 如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6 18
S A B C D T
0 1 1
0 3 2
0 4 5
1 0 1
1 2 2
1 4 5
2 1 2
2 4 1
2 5 4
3 0 2
3 4 3
4 0 5
4 1 5
4 2 1
4 3 3
4 5 1
5 2 4
5 4 1
  • 通过g++进行构建
1
g++ Dijkstra.cpp -o Dijkstra
  • 更新：基于优先级队列实现的 Dijkstra 算法存在问题，priority_queue<vertexnode*, vector<vertexnode*="">, cmp> vertexQueue; 优先级队列保存的是节点的指针，为了保证从队头都能取得距离源点距离最近的节点，同一个节点（不同的距离值）会被重复入队；然而由于存入的是指针，对即将入队的节点的松弛操作同样会影响到先前入队的同一个节点（不同的距离值），破坏了原先的优先队列顺序（可能是基于 heap 实现），造成优先级队列操作异常，故修正为如下代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
#include <queue>
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  int weight;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
  char data;
  int vertexIdx;
  adjVertexNode* list;
  int dist;
  // How to restore a shortest path: recording the pre-visit VertexNode in the path
  VertexNode* preVertexNode;
  /* reload compare operator for priority queue
	 * In order to achieve the minimum heap(in ascending order)
	 *   reload operator<, redefine the priority to smaller one
	 */
  bool operator< (const VertexNode& right) const {
    return dist > right.dist;
  }
};
 
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
 
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].vertexIdx = i;
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
void Dijkstra(Graph& g, VertexNode& Source) {
  priority_queue<VertexNode> vertexQueue;
  bool visited[g.vertexNum];
  for(int i=0; i<g.vertexNum; i++) {
    g.VertexNodes[i].dist = INT_MAX;
    g.VertexNodes[i].preVertexNode = NULL;
    visited[i] = false;
  }
 
  Source.dist = 0;
  // void push( const value_type& value );
  vertexQueue.push(Source);
 
  while(!vertexQueue.empty()) {
    VertexNode v = vertexQueue.top();
    // cout << "pop: " << v.data << " ";
    vertexQueue.pop();
 
    int vertexIdx = v.vertexIdx;
    if(visited[vertexIdx]) {
      continue;
    }
    visited[vertexIdx] = true;
 
    adjVertexNode* head = v.list;
    // cout << "push: ";
    // relax operation: update the estimated distance for all adjacent vertex 
    while (head != NULL) {
      /*
			 * A node with different dist will be pushed repeatedly for smallest one
			 *  use visited(visited[vertexIdx]) flag to avoid not-smallest visit
			 * A node in known-region should't be repeatedly updated 
			 *	use visited[head->adjVertexIdx]
			 */ 
      if(!visited[head->adjVertexIdx] && g.VertexNodes[head->adjVertexIdx].dist 
        > (v.dist + head->weight)) {
        g.VertexNodes[head->adjVertexIdx].dist = v.dist + head->weight;
        g.VertexNodes[head->adjVertexIdx].preVertexNode = &g.VertexNodes[v.vertexIdx];
        vertexQueue.push(g.VertexNodes[head->adjVertexIdx]);
        // cout << g.VertexNodes[head->adjVertexIdx].data << " ";
      }
      head = head->next;
    }
    // cout << endl;
  }
}
 
// backtracking for the path
void PrintPath(Graph& g, VertexNode* target) {
  if (target->preVertexNode != NULL) {
    PrintPath(g, target->preVertexNode);
    cout << "->";
  }
  cout << target->data;
}
 
int main(int argc, const char** argv) {
  //freopen("Dijkstra.txt", "r", stdin);
  freopen("BellmanFord.txt", "r", stdin);
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  cout << endl;
  cout << "  Source=>Target\tShortest Distance\tPath" << endl;
  for(int from=0; from<g.vertexNum; from++) {
    Dijkstra(g, g.VertexNodes[from]);
    for(int to=0; to<g.vertexNum; to++) {
      if(from == to) {
        continue;
      }
      cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data 
        << "\t\t\t";
      if(g.VertexNodes[to].dist == INT_MAX) {
        cout << "INF";
      }else {
        cout << g.VertexNodes[to].dist;
      }
      cout << " \t\t(";
      PrintPath(g, &g.VertexNodes[to]);
      cout << ")" << endl;
    }
    cout << endl;
  }
   
  DeleteGraph(g);
  return 0;
}

Bellman-Ford 算法

References:

  • 查看从 s 到 t 的最短路径
    • 该路径最多含有 $|V|-1$ 条边。
      • 因为最短路径肯定是个简单路径，不可能包含回路的：如果包含回路，且回路的权值和为正的，那么去掉这个回路，可以得到更短的路径；如果回路的权值是负的，那么肯定没有解了
      • 图有 $|V|$ 个点，又不能有回路，所以最短路径最多 $|V|-1$ 边
    • 如果执行的更新操作按照以下顺序 $(s, u_1), (u_, u_2), …, (u_k, t)$（更新序列） 进行（只要保证上述更新操作全部按顺序执行即可，并不要求上述更新操作是连续进行的），最终 t 的最短路径一定是正确的。
      • 最短路的局部最优性：中间即便穿插其它 update 操作，也不会影响最短路径。
      • 其它 update 操作是否在这些边上进行无关紧要，同样，图上其它部分进行的 update 操作也不对上述最短路产生影响。
      • 即，update 操作是安全的。
    • Dijkstra 算法所运行的更新序列是经过选择的。
      • 选择基于这一假设：从起始点 s 到任意顶点 v 的最短路径一定会经过比 v 距离 s 更近的顶点。
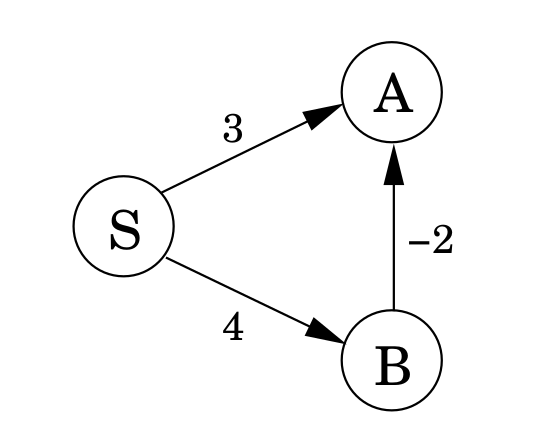
      • 当边的长度可以为负值时，这一假设将不再成立，如下图：从 S 到 A 的最短路径经过 B，而 B 却比 A 距离 S 更远！
    • 为了求出负权图的最短路径，我们需要保证一个合理的更新序列。但是：我们预先并不知道所求的最短路径（如 s->t），因此不能确保按照正确的顺序更新了正确的边（$s→u_1, u_1→u_2, …, u_k→t$）
      • 解决方案：每次迭代更新所有的边
        • 由于多余的更新操作总是无害的，因此算法（几乎）可以正确运行。
        • 每条边更新 $|V|-1$ 次（任何含有 $|V|$ 个顶点的图两个点之间的最短路最多含有 $|V|-1$ 条边，每次迭代均能找到从起始点 s 出发的最短路上的一条边），时间复杂度为 $O(|V|·|E|)$
        • 如果某次循环没有更新操作发生，后续的迭代也不会有更新操作，可以利用这一性质避免无效的计算。
    • 算法实现中唯一一个需要注意的问题就是负值圈 (negative-cost cycle)。
      • 负值圈指的是，权值总和为负的圈。如果存在这种圈，我们可以在里面滞留任意长而不断减小最短路径长，因此这种情况下最短路径是不存在的。
      • 对于 Bellman-Ford 算法来说，判断负值圈存在的方法是：在 $|V|-1$ 次循环之后再执行一次循环，如果还有更新操作发生，则说明存在负值圈。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  // weight: length on edges
  int weight;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
  char data;
  adjVertexNode* list;
  int dist;
  // How to restore a shortest path: recording the pre-visit VertexNode in the path
  VertexNode* preVertexNode;
};
  
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
  
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].preVertexNode = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
bool BellmanFord(Graph& g, VertexNode& Source) {
  for(int i=0; i<g.vertexNum; i++) {
    g.VertexNodes[i].dist = INT_MAX;
    g.VertexNodes[i].preVertexNode = NULL;
  }
 
  Source.dist = 0;
  for (int vertexNum=0; vertexNum<=g.vertexNum; vertexNum++) {
    bool updated = false;
    // update all edges
    for(int VertexIdx=0; VertexIdx<g.vertexNum; VertexIdx++) {
      adjVertexNode* head = g.VertexNodes[VertexIdx].list;
      while (head != NULL) {
        if(g.VertexNodes[VertexIdx].dist != INT_MAX
          && g.VertexNodes[head->adjVertexIdx].dist > (g.VertexNodes[VertexIdx].dist + head->weight)) {
          g.VertexNodes[head->adjVertexIdx].dist = g.VertexNodes[VertexIdx].dist + head->weight;
          g.VertexNodes[head->adjVertexIdx].preVertexNode = &g.VertexNodes[VertexIdx];
          updated = true;
        }
        head = head->next;
      }
    }
    // shortest path got after any round which no update occurred
    if(!updated) {
      return true;
    }
    // negative cycles exist
    if(vertexNum == g.vertexNum && updated) {
      return false;
    }
  }
  // should never reach here
  return false;
}
 
// backtracking for the path
void PrintPath(Graph& g, VertexNode* target) {
  if (target->preVertexNode != NULL) {
    PrintPath(g, target->preVertexNode);
    cout << "->";
  }
  cout << target->data;
}
 
int main(int argc, const char** argv) {
  //freopen("Dijkstra.txt", "r", stdin);
  freopen("BellmanFord.txt", "r", stdin);
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  cout << endl;
  cout << "  Source=>Target\tShortest Distance\tPath" << endl;
  for(int from=0; from<g.vertexNum; from++) {
    if(!BellmanFord(g, g.VertexNodes[from])) {
      cout << "Failed to find shortest path: negative cycles exist..." << endl;
      break;
    }
    for(int to=0; to<g.vertexNum; to++) {
      if(from == to) {
        continue;
      }
      cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data 
        << "\t\t\t" << g.VertexNodes[to].dist << " \t\t(";
      PrintPath(g, &g.VertexNodes[to]);
      cout << ")" << endl;
    }
    cout << endl;
  }
   
  DeleteGraph(g);
  return 0;
}
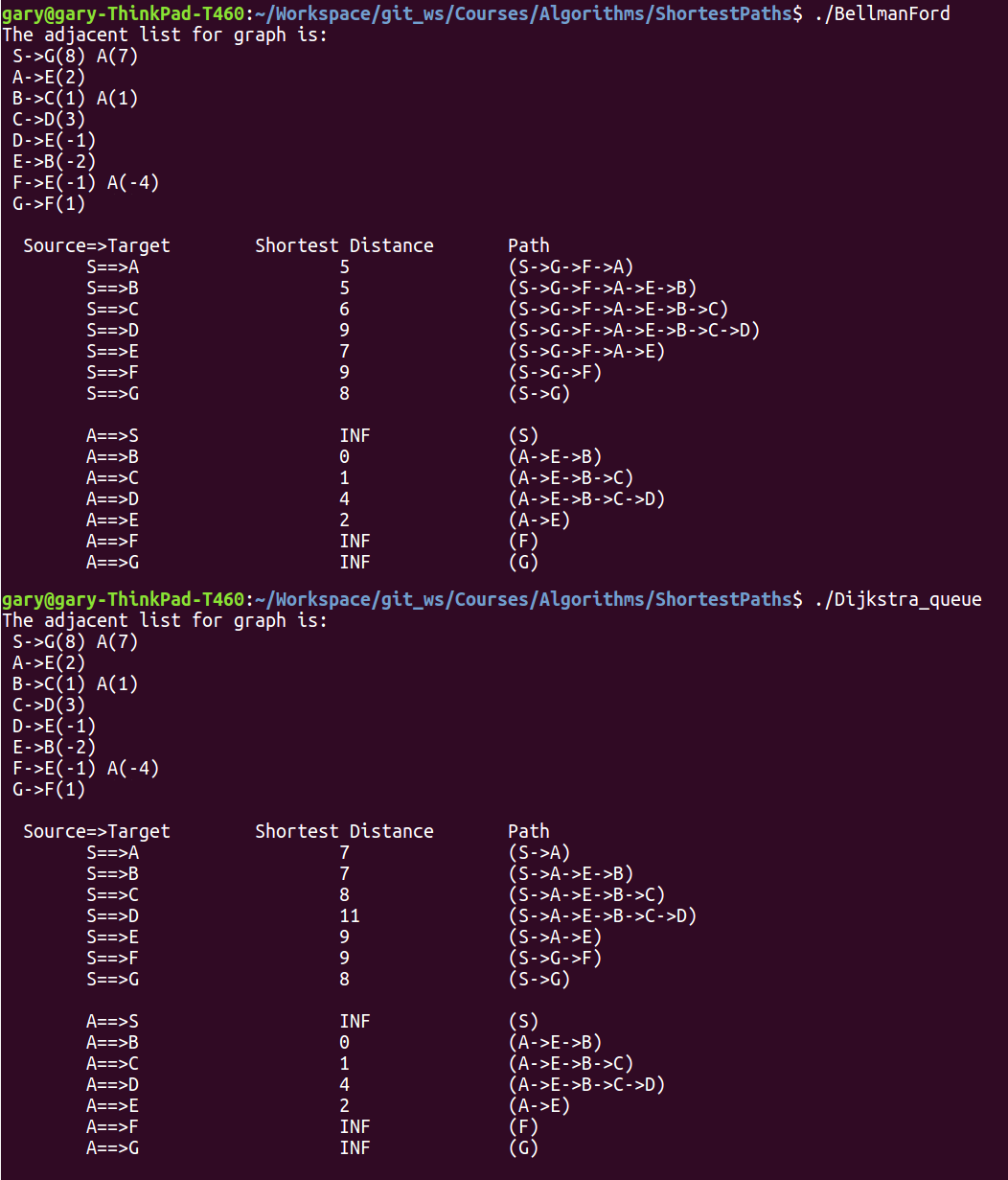
  • 对于非负权图 Bellman-Ford 算法和 Dijkstra 算法都能得到相同的正确解。

  • Dijkstra 算法难以处理负权图的最短路径问题，主要原因便是上面提到的前提假设不成立，比如，S 到 A 的最短路经过 $(S, G)$，然而 $|(S, A)| < |(S, G)|$。
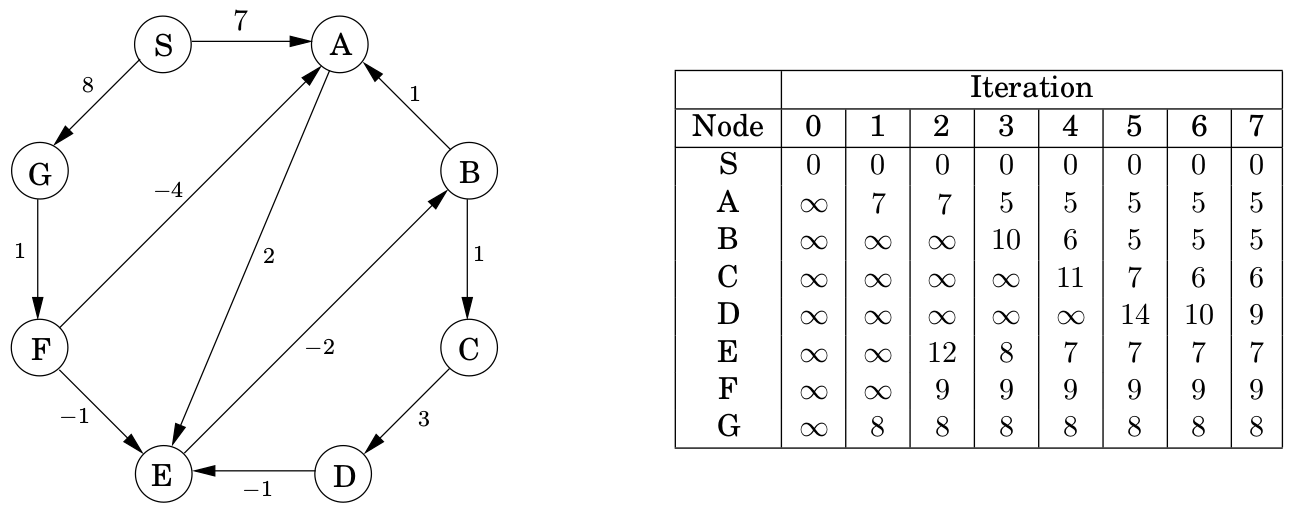
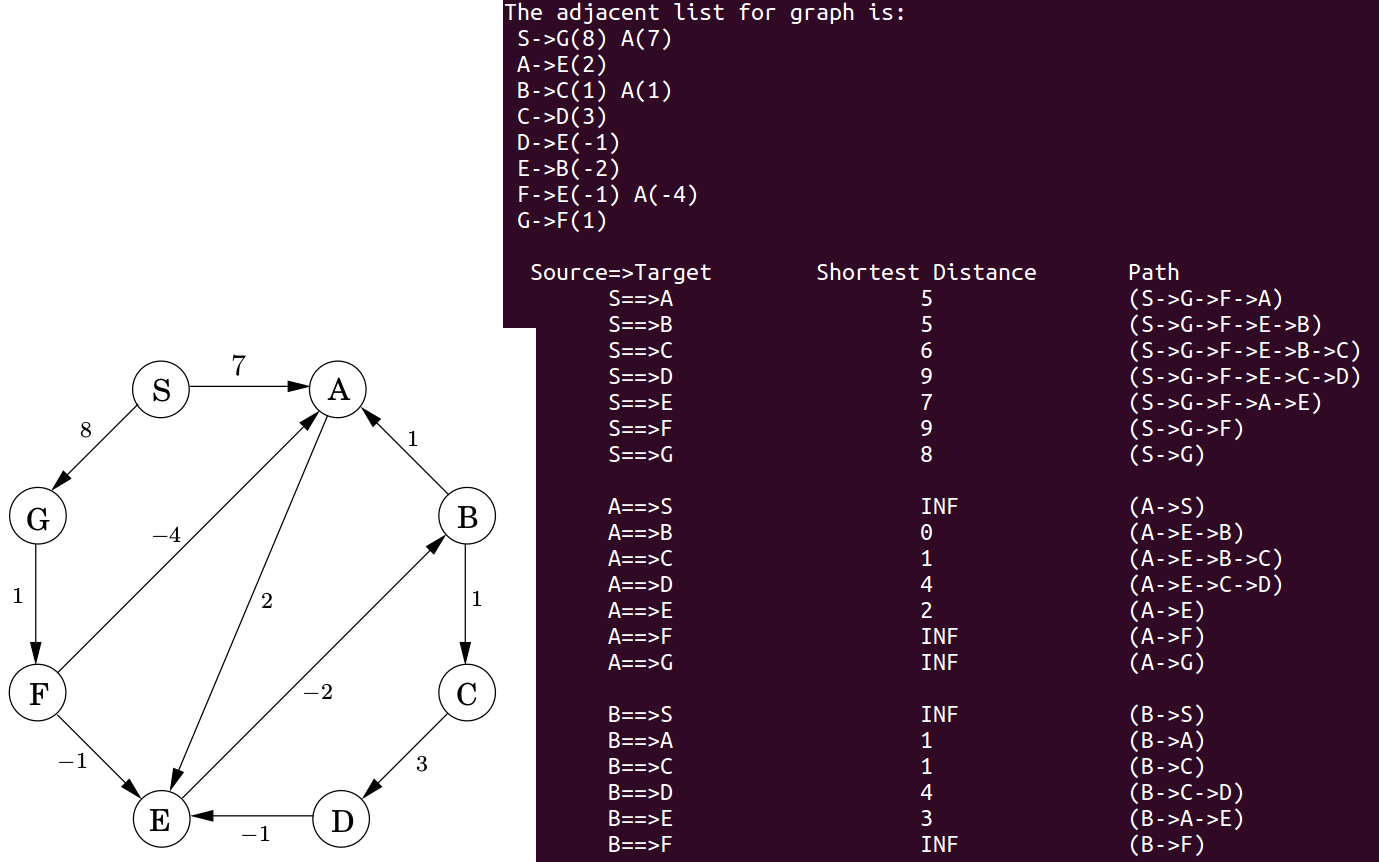
  • 上图对应的输入文件 BellmanFord.txt 如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
8 12
S A B C D E F G
0 1 7
0 7 8
1 5 2
2 1 1
2 3 1
3 4 3
4 5 -1
5 2 -2
6 1 -4
6 5 -1
7 6 1

Floyd-Warshall 算法

References:

  • 解决单源最短路径问题的方案有 Dijkstra 算法和 Bellman-Ford 算法，对于全源最短路径问题（All-Pairs Shortest Paths Problem）可以认为是单源最短路径问题（Single Source Shortest Paths Problem）的推广，即分别以每个顶点作为源顶点并求其至其它顶点的最短距离（如运行Bellman-Ford 最短路径算法（由于可能存在负边），这样下来总的运行时间将是$O(|V|^2 E)$，事实上有一种稍好的选择，其运行时间为$O(|V|^3)$，正是本节介绍的基于动态规划的 Floyd-Warshall 算法）。
  • Floyd-Warshall 算法采用动态规划方案来解决在一个有向图（无向图可以转化为双向有向） G = (V, E) 上每对顶点间的最短路径问题，即全源最短路径问题，其中图 G 允许存在权值为负的边，但不存在权值为负的回路。
  • Floyd-Warshall 算法思想
    • 最短路径算法中的最优子结构：两顶点之间的最短路径包含路径上其它顶点的最短路径。
      • 具体描述为：对于给定的带权图 $G = (V, E)$，设 $p = \lt v_1, v_2, …,v_n \gt$ 是从 $v_1$ 到 $v_n$ 的最短路径，那么对于任意 i 和 j，$1≤i≤j≤n, p_{ij} (shortestPath(i, j, k)) = \lt v_i, v_{i+1}, …, v_j \gt$ 为 p 中从顶点 $v_i$ 到 $v_j$ 的一条子路径，那么 $p_{ij}$ 是顶点 $v_i$ 到 $v_j$ 的最短路径。
    • 从任意节点 i 到任意节点 j 的最短路径不外乎2种可能：①直接从 i 到 j；②从 i 经过若干个中间节点 k 到 j。
      • dist(i, j, k)：从顶点 i 到 j 的仅使用节点 ${1, 2, …, k}$ 作为中间节点的最短路径长度。
      • $ dist(i, j, 0) = \begin{cases} |E(i, j)| \cr \infty, else \end{cases} $
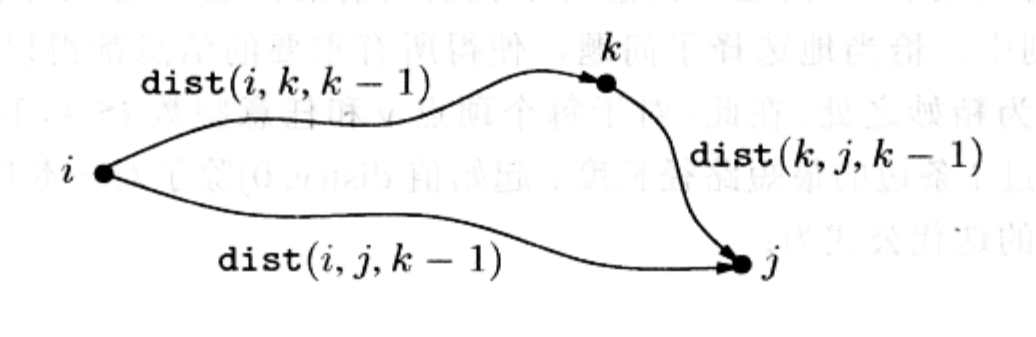
      • 当我们在中间节点集中加入一个新的顶点 k 时，需要对所有的节点对 $(i，j)$ 检查是否使用 k 作为中间节点会得到更短的路径。$i → j $ 的使用了 k 和其它编号较小（＜k）的中间节点的最短路径最多经过 k 一次（假设没有负环），通过使用已经计算得到的 i 到 k 和 k 到 j 的使用了较小编号顶点的最短路径长度能够求解 $i → j $ 的最短路径长度。
      • $ shortestPath(i, j, k) = min(shortestPath(i, j, k-1), shortestPath(i, k, k-1) + shortestPath(k, j, k-1))$
    • Floyd-Warshall 算法的设计基于了如下观察。设带权图 G = (V, E) 中的所有顶点 V = {1, 2, . . . , n}，考虑一个顶点子集 {1, 2, . . . , k}。对于任意对顶点 i, j，考虑从顶点 i 到 j 的所有路径的中间顶点都来自该子集 {1, 2, . . . , k}，设 p 是该子集中的最短路径。Floyd-Warshall 算法描述了 p 与 i, j 间最短路径及中间顶点集合 {1, 2, . . . , k - 1} 的关系，该关系依赖于 k 是否是路径 p 上的一个中间顶点。
      • ①②：不允许路径 $i → j$ 上出现任何的中间节点；不存在直接连接 i 和 j 的边时，$dist(i, j, 0) = \infty$。
      • ③：注意 k，i，j 三重循环的顺序，算法的时间复杂度为 $O(|V|^3)$；另外，$dist(?, ?, k)$ 只与 $dist(?, ?, k-1)$ 有关，使用二维数组即可维护只使用 {1, 2, …, k-1, k} 作为中间节点的最短距离信息，无需开辟三维空间，空间复杂度为 $O(|V|^2)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
#include <iostream>   
#include <stdio.h>			// for stdin
#include <limits.h>			// for INT_MAX
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
struct adjVertexNode {
  int adjVertexIdx;
  // weight: length on edges
  int weight;
  adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 8(16)
struct VertexNode {
  char data;
  adjVertexNode* list;
};
  
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
  
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].list = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
 
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
bool FloydWarshall(Graph& g, int dists[][MAX_VERTEX_NUM], int paths[][MAX_VERTEX_NUM]) {
  // dists[i][j]=INT_MAX; dists[i][i]=0;
  for(int i=0; i<g.vertexNum; i++) {
    for(int j=0; j<g.vertexNum; j++) {
      dists[i][j] = (i==j)? 0:INT_MAX;
      paths[i][j] = j;
    }
  }
  // edge<i,j> exists, update dists[i][j]=|edge<i,j>|
  for(int VertexIdx=0; VertexIdx<g.vertexNum; VertexIdx++) {
    adjVertexNode* head = g.VertexNodes[VertexIdx].list;
    while (head != NULL) {
      dists[VertexIdx][head->adjVertexIdx] = head->weight;
      head = head->next;
    }
  }

  for(int k=0; k<g.vertexNum; k++) {
    for(int i=0; i<g.vertexNum; i++) {
      for(int j=0; j<g.vertexNum; j++) {
        if(dists[i][k] != INT_MAX && dists[k][j] != INT_MAX
          && (dists[i][k] + dists[k][j]) < dists[i][j]) {
          dists[i][j] = dists[i][k] + dists[k][j];
          paths[i][j] = k;
          // negative cycle exists when and only when dists[i][i]<0
          if(i == j && dists[i][j] < 0) {
            return false;
          }
        }
      }
    } 
  }
  return true;
}
 
// backtracking for the path
void PrintPath(Graph& g, int paths[][MAX_VERTEX_NUM], int fromIdx, int toIdx) {
  int vertexIdx = fromIdx;
  while(vertexIdx != toIdx) {
    cout << g.VertexNodes[vertexIdx].data << "->";
    vertexIdx = paths[vertexIdx][toIdx];
  }
  cout << g.VertexNodes[vertexIdx].data;
}
 
int main(int argc, const char** argv) {
  //freopen("Dijkstra.txt", "r", stdin);
  freopen("BellmanFord.txt", "r", stdin);
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
 
  int dists[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
  int paths[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
 
  cout << endl;
  if(!FloydWarshall(g, dists, paths)) {
    cout << "Failed to find shortest path: negative cycles exist..." << endl;
  }
  else {
    cout << "  Source=>Target\tShortest Distance\tPath" << endl;
    for(int from=0; from<g.vertexNum; from++) {
      for(int to=0; to<g.vertexNum; to++) {
        if(from == to) {
          continue;
        }
        cout << "\t" << g.VertexNodes[from].data << "==>" << g.VertexNodes[to].data 
          << "\t\t\t";
        if(dists[from][to] == INT_MAX) {
          cout << "INF";
        }else {
          cout << dists[from][to];
        }
        cout << " \t\t(";
        PrintPath(g, paths, from, to);
        cout << ")" << endl;
      }
      cout << endl;
    }
  }
   
  DeleteGraph(g);
  return 0;
}
  • dists[][] 数组初始化为各顶点间的原本距离（不存在直连边时距离为 $\infty$），最后存储各顶点间的最短距离。
  • paths[][] 数组保存最短路径，与当前迭代的次数有关。初始化都为目标顶点下标，表示没有中间顶点。在求 dists[i][j] 过程中，paths[i][j] 存放从顶点$v_i$ 到顶点 $v_j$ 的中间顶点编号不大于 k 的最短路径上前一个结点的编号。在算法结束时，由二维数组 paths 的值回溯，可以得到从顶点 $v_i$ 到顶点 $v_j$ 的最短路径。
  • 通过 g++ 进行构建
1
g++ FloydWarshall.cpp -o FloydWarshall
  • Floyd-Warshall 算法 适用于非负权无向图
  • Floyd-Warshall 算法 同样适用于负权有向图

本文标题:算法设计与分析[0006] Some Shortest-path Algorithms（最短路径算法）

文章作者:Gary

发布时间:2017-03-29, 14:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/03/29/Algorithms_Some Shortest-path Algorithms/

文章目录
  1. 1. Breadth-first Search 无权最短路径算法
  2. 2. Dijkstra 算法
  3. 3. Bellman-Ford 算法
  4. 4. Floyd-Warshall 算法