算法设计与分析[0011] Dynamic Programming(III)（Longest Common Subsequence）

编程珠玑Algorithm

　　子序列和子字符串的不同之处在于，子序列不需要是原序列上连续的字符。对于 Longest Common Substring 以及 Longest Common Subsequence 这类题目，大多数需要用到 DP 的思想，其中，状态转移是关键。

最长公共子字符串

Given two strings, find the longest common substring.
Return the length of it.

  • Example
    　Given A = “ABCD”, B = “CBCE”, return 2.
  • $L(idxA, idxB)$：以 $A[idxA]$ 和 $B[idxB]$ 结尾的相同子字符串的最长长度。最长公共子字符串必然存在所有情况中以 A 序列中某个字符结尾，以 B 序列中某个字符结尾的一种情况，所以取所有可能情况中的最大值即为 Longest Common Substring 的长度。
    • 因为要求子串连续，所以对于 $A_{idxA}$ 与 $B_{idxB}$ 来讲，它们要么与之前的公共子串构成新的公共子串；要么就是不构成公共子串。
      $$ L(idxA, idxB) = \begin{cases}
      if（idxA==0||idxB==0）: \begin{cases} 1, A[idxA]==B[idxB] \cr 0, others \end{cases} \cr
      else-if（A[idxA]==B[idxB]）: L(idxA-1, idxB-1) + 1 \cr
      else: 0
      \end{cases}
      $$
    • 上述过程的示例图如下，可以看出只有对角线方向上的长度延伸，长度不能保留。
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      class Solution {
      public: 
          /**
           * @param A, B: Two string.
           * @return: the length of the longest common substring.
           */
          int longestCommonSubstring(string &A, string &B) {
              int lenA = A.length();
              int lenB = B.length();
              if(lenA==0 || lenB==0) {
                  return 0;
              }
              // L[idxA][idxB]: the largest length of LCS ending with A[idxA] and B[idxB] 
              int L[lenA][lenB];
              for(int idxB=0; idxB<lenB; idxB++) {
                  L[0][idxB] = B[idxB]==A[0]? 1 : 0; 
              }
              for(int idxA=0; idxA<lenA; idxA++) {
                  L[idxA][0] = A[idxA]==B[0]? 1 : 0; 
              }
              
              for(int idxA=1; idxA<lenA; idxA++){
                  for(int idxB=1; idxB<lenB; idxB++){
                      L[idxA][idxB] = A[idxA]==B[idxB]? L[idxA-1][idxB-1]+1 : 0;
                  }
              }
              
              int maxLen = 0;
              int maxLenIdx = -1;
              for(int idxA=0; idxA<lenA; idxA++){
                  for(int idxB=0; idxB<lenB; idxB++){
                      if(L[idxA][idxB] > maxLen) {
                          maxLen = L[idxA][idxB];
                          maxLenIdx = idxA;
                      }
                  }
              }
              return maxLen;
          }
      };
  • 提取最长公共子串
    • 使用变量 maxLenIdx 记录最长公共子串（长度 maxLen ）对应的结尾字符下标（序列 A/B 都可以），回退获取 maxLen 个字符即可。

最长公共子序列

Given two strings, find the longest common subsequence (LCS).
Your code should return the length of LCS.

  • Example
    　For “ABCD” and “EDCA”, the LCS is “A” (or “D”, “C”), return 1.
    　For “ABCD” and “EACB”, the LCS is “AC”, return 2.
  • $L(idxA, idxB)$：以 $A_{idxA}$ 结尾的子串（$A[0, 1, …, idxA], 0 \leq idxA \lt len_A$） 和 $B_{idxB}$ 结尾的子串（$B[0, 1, …, idxB], 0 \leq idxB \lt len_B$）最长公共子序列的长度。自然地，$L(len_A-1, len_B-1)$ 即为所求的最长公共子序列长度。
  • 与子串不同，子序列可以是不连续的。
    • $L(idxA, idxB)$ 与 $L(idxA-1, idxB-1)$ 两者其实只差 $A_{idxA}$ 和 $B_{idxB}$ 这一对字符。
    • 如果 $A_{idxA}$ 和 $B_{idxB}$ 相同，那么就只要在以 $A_{idxA}$ 和以 $B_{idxB}$ 结尾的两个子串的最长公共子序列之后添上这个相同字符即可，这样就可以让长度增加一位。
    • 如果 $A_{idxA}$ 和 $B_{idxB}$ 不同，两个子串在末尾添加一个字符后最长公共子序列并不能得到延伸。考虑到 $A_{idxA}$ 可能与 $B_{idxB-1}$ 相同或者 $B_{idxB}$ 会与 $A_{idxA-1}$ 相同，没能延伸的最长公共子序列只能在 $L(idxA, idxB-1)$ 和 $L(idxA-1, idxB)$ 存在，取更长的那个。
    • 结合边界限制，最终得到的状态转移方程如下：
      $$ L(idxA, idxB) = \begin{cases}
      if（idxA==0）: \begin{cases} 1, B[idxB]==A[0] \cr L(0, idxB-1), others \end{cases} \cr
      else·if（idxB==0）: \begin{cases} 1, A[idxA]==B[0] \cr L(idxA-1, 0), others \end{cases} \cr
      else·if（A[idxA]==B[idxB]）: L(idxA-1, idxB-1) + 1 \cr
      else: max(L(idxA, idxB-1), L(idxA-1, idxB))
      \end{cases}
      $$
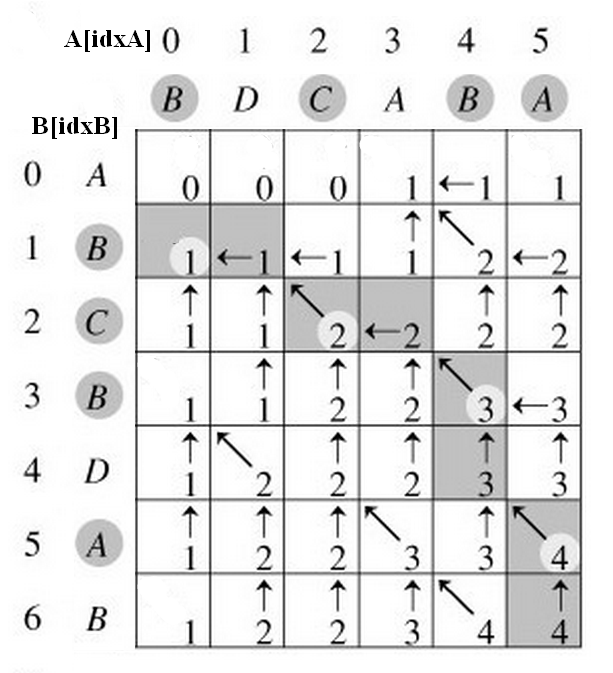
    • 上述过程的示例图如下，可以看出同样只有对角线方向上的长度延伸，不过长度可以在 上→下 和 左→右 方向上得到保留。
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      42
      43
      44
      45
      46
      47
      48
      49
      50
      51
      52
      53
      54
      55
      56
      57
      58
      #define max(a,b) (a>b?a:b)
      class Solution {
      public:
          /**
           * @param A, B: Two strings.
           * @return: The length of longest common subsequence of A and B.
           */
          int longestCommonSubsequence(string A, string B) {
              int lenA = A.length();
              int lenB = B.length();
              if(lenA==0 || lenB==0) {
                  return 0;
              }
              // L[idxA][idxB]: the length of the LCS ending with A[idxA] and B[idxB]
              int L[lenA][lenB];
              // for recording LCS's tail element index
              int maxLen = 0, maxLenIdxA = 0, maxLenIdxB = 0;
              
              L[0][0] = A[0]==B[0]? 1 : 0;
              for(int idxB=1; idxB<lenB; idxB++) {
                  L[0][idxB] = B[idxB]==A[0]? 1 : L[0][idxB-1];
                  
                  // for recording LCS's tail element index
                  if(L[0][idxB] > maxLen) {
                      maxLen = L[0][idxB];
                      maxLenIdxB = idxB;
                  }
              }
              for(int idxA=1; idxA<lenA; idxA++) {
                  L[idxA][0] = A[idxA]==B[0]? 1 : L[idxA-1][0];
                  
                  // for recording LCS's tail element index
                  if(L[idxA][0] > maxLen) {
                      maxLen = L[idxA][0];
                      maxLenIdxA = idxA;
                  }
              }
              
              for(int idxA=1; idxA<lenA; idxA++) {
                  for(int idxB=1; idxB<lenB; idxB++) {
                      if(A[idxA] == B[idxB]) {
                          L[idxA][idxB] = L[idxA-1][idxB-1] + 1;
                      }
                      else {
                          L[idxA][idxB] = max(L[idxA][idxB-1], L[idxA-1][idxB]);
                      }
                      
                      // for recording LCS's tail element index
                      if(L[idxA][idxB] > maxLen) {
                          maxLen = L[idxA][idxB];
                          maxLenIdxA = idxA;
                          maxLenIdxB = idxB;
                      }
                  }
              }
              return L[lenA-1][lenB-1];
          }
      };
  • 提取最长公共子序列
    • 使用变量 maxLen 记录最长公共子序列的长度，并通过变量 maxLenIdxA 和 maxLenIdxB 记录该最长长度序列末尾字符对应的序列 A 和序列 B 中的字符下标。
    • 在序列 A 和 B 中分别从下标 maxLenIdxA 和 maxLenIdxB 向左挪动，找出 maxLen 个相同字符，即为提取的最长公共子序列。
    • 如何在序列 A 和 B 中向左挪动呢？
      • A[maxLenIdxA]==B[maxLenIdxB]，当前字符相同，同时左挪（因为公共子序列的特点，此时二者肯定均为到达边界）：maxLenIdxA-- & maxLenIdxB--。
      • A[maxLenIdxA]!=B[maxLenIdxB]，当前字符不相同
        • 有挪动到边界（0）的，只能挪动另一个还没到边界的；假如同时挪动到边界，由于 maxLen 的准确性，说明已经提取出最长公共子序列。
        • L[idxA][idxB-1] 大，说明 A[maxLenIdxA] 可能与序列 B 中下一个字符相同，需要挪动序列 B：maxLenIdxB--；反之，则需要挪动序列 A：maxLenIdxA--。
    • 具体的代码实现如下：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      string LCS;
      while(maxLenIdxA>=0 && maxLenIdxB>=0) {
          if(A[maxLenIdxA] == B[maxLenIdxB]) {
              LCS += A[maxLenIdxA];
              maxLenIdxA--;
              maxLenIdxB--;
          }
          else {
              if(maxLenIdxA == 0) {
                  maxLenIdxB--;
              }
              else if(maxLenIdxB == 0) {
                  maxLenIdxA--;
              }
              else {
                  if(L[maxLenIdxA][maxLenIdxB-1] < L[maxLenIdxA-1][maxLenIdxB]) {
                      maxLenIdxB--;
                  }
                  else {
                      maxLenIdxA--;
                  }
              }
          }
      }

本文标题:算法设计与分析[0011] Dynamic Programming(III)（Longest Common Subsequence）

文章作者:Gary

发布时间:2017-05-03, 14:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/05/03/Algorithms_LongestCommonSubsequence/

文章目录
  1. 1. 最长公共子字符串
  2. 2. 最长公共子序列