网络流:最大流问题
- 所谓网络:
- 一个有向图 $G=(V, E)$
- G中有两个特殊节点 $s, t \in V$,分别称为 G 中的源点(source) 和汇点(sink)。
- G中每条边都有容量 $c_e \lt 0$。
- 所谓流是指一种特定的输送方式,其中对每条边赋予一个变量 $f_e$,使其满足如下三个基本性质:
- 容量限制(Capacity Constraints):不超过边的容量,即对所有 $e \in E, 0 \leq f_e \leq c_e$
- 流量守恒(Flow Conservation):对于 s 和 t 之外的任意节点 u,输入 u 的流量等于输出 u 的流量(流量是守恒的):$\sum_{(w, u) \in E} f_{wu} = \sum_{(u, z) \in E} f_{uz} $
- 斜对称性(Skew Symmetry):$ f_{uv} = -f_{vu}$
- 网络流问题(NetWork Flow Problem)
- 给定指定的一个有向图,其中有两个特殊的点:源 S 和汇 T,每条边有指定的容量(Capacity),求满足条件的从 S 到 T 的最大流(MaxFlow)。
- 最大流
- 流的规模为由 s 流向 t 的总流量,由上面的流量的守恒律,其等于离开 s 的流量。
- 目标函数(最大化):$ 规模(f) = \sum_{(s, u) \in E} f_{su} = \sum_{(z, t) \in E} f_{zt} $
- 其他相关定义
- 容量网络(capacity network)&流量网络(flow network)&残留网络(residual network)
- 网络就是有源、汇的有向图,关于什么的网络就是指边权的含义是什么。
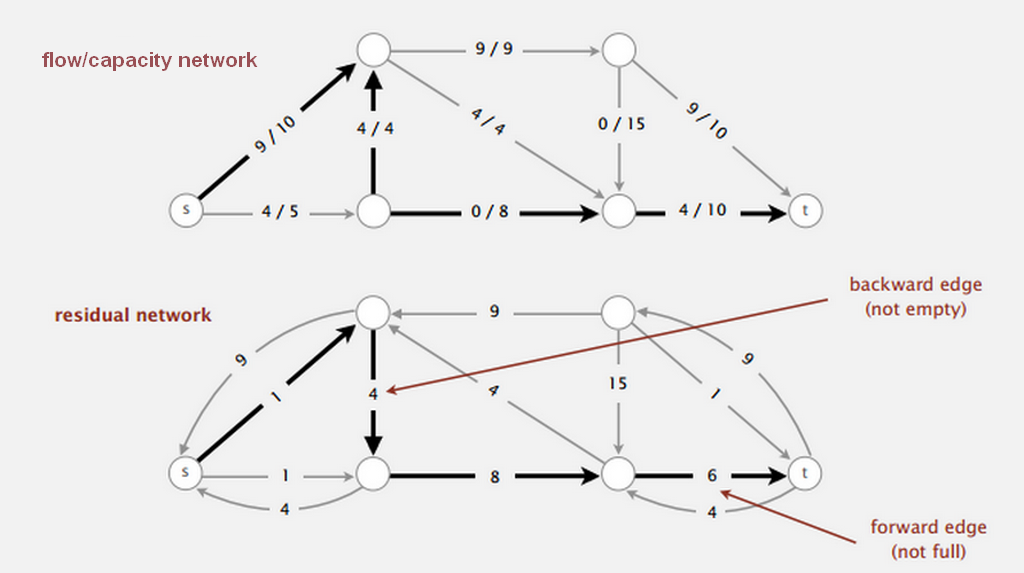
- 容量网络就是关于容量的网络。在求解问题的过程中,容量网络基本是不改变的。
- 流量网络就是关于流量的网络。在求解问题的过程中,流量网络通常在不断改变,但是总是满足上述三个性质;调整到最后就是最大流网络,同时也可以得到最大流值。
- 残量网络往往概括了容量网络和流量网络,是最为常用的,残量网络=容量网络-流量网络。
- 网络就是有源、汇的有向图,关于什么的网络就是指边权的含义是什么。
- 增广路径(Augmenting path):增广路径顾名思义就是能够增加流量的路径。增广路径 p 是残量网络中一条从源点 s 到汇点 t 的简单路径,在一条增广路径 p 上能够为每条边增加的流量的最大值为路径 p 的 残存容量(remaining capacity):$c_f(p) = min \verb|{| c_f(u,v):(u,v) \in p \verb|}|$
- 割&割集
- 一个无向连通网络,去掉一个边集可以使其变成两个连通分量,则这个边集就是割集
- 无向图的割集(Cut Set):$C[A,B]$ 是将图 G 分为 A 和 B 两个点集(连通分量)的连接 A 和 B 之间的边的全集。
- 带权图的割(Cut) 就是割集中边或者有向边的权和。
- 最小割集当然就是权和最小的割集。
- 在有向图网络 $G(V, E)$ 中, 割(S, T) 将 V 划分为 S 和 T=V-S,使得 s 属于 S 集合,t 属于 T 集合,割(S, T) 的容量是指从集合 S 到集合 T 所有边的容量之和。
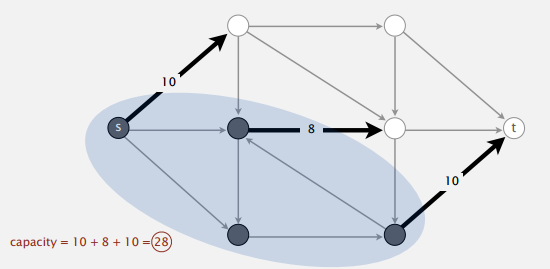
- 一个无向连通网络,去掉一个边集可以使其变成两个连通分量,则这个边集就是割集
- 容量网络(capacity network)&流量网络(flow network)&残留网络(residual network)
最大流问题与线性规划
最大流问题可以转换为线性规划问题,而线性规划问题最著名的解法自然就是 单纯形法。这种算法非常奇特,其复杂度为在最坏情况下是指数级的,但其在实践中绝大多数的情况下表现出的效率非常令人满意。
- 设$c_{uv}$ 代表边 u 到 v 最大允许的流量(capacity),$f_{uv}$ 代表 u 到 v 当前流量。
- 最大流可以表示为:
$$
\Large{max}
\normalsize{ \sum_{u:(s, u) \in E} f_{su} \quad }
\Large{s.t.} \normalsize{
\begin{cases} 0 \leq f_{uv} \leq c_{uv}, \forall (u, v) \in E \cr
\sum_{w:(w, u) \in E} f_{wu} - \sum_{v:(u, v) \in E} f_{uv} = 0, \forall u \in V \backslash \verb|{| s, t \verb|}| \end{cases}
}
$$ - 事实上,使用 单纯形法 解决网络最大流问题非常直观:
- 从零流量开始
- 重复下述过程:
- 选择一条从源点 s 到汇点 t 的合适路径
- 将该路径的流量增加到无法增加为止
- 每次迭代单纯形法寻找到 s→t 的一条路径,路径中的边有两种类型(如下图(b)中右图所示,可以同时存在这两种类型的边):
① 边在最初的网络中,且未达到最大流量,如下图(b)右图中的边 a→d;
② 边的反向边在最初的网络中,如下图(c)右图中的边 d→a。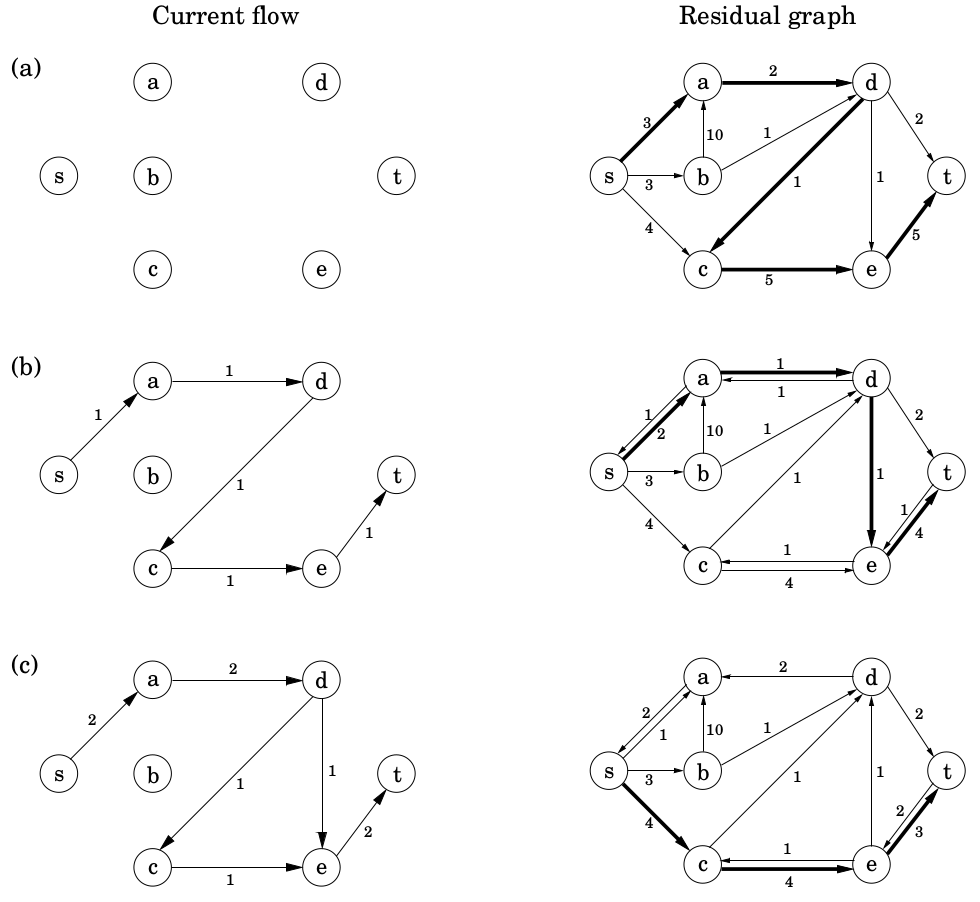
- 如果当前的流为 $f$,则对于第①种情况,边 $(u, v)$ 最多还能接受 $c_{uv} - f_{u, v}$ 的多余流量;而在第②种情况,最多增加的流量为 $f_{vu}$(取消 $(v, u)上的全部或部分流量$ )。
- 这类增加流量的机会可以由 残量网络 $G^f=(V, E^f)$ 来判定,该网络包含了所有的以上两种边,并标出了每条边的剩余流量:
$$
c^f =
\begin{cases} c_{uv} - f_{uv}, \quad 若(u, v) \in E 且 f_{uv} \lt c_{uv} \cr
f_{vu}, \qquad \quad 若(v, u) \in E 且 f_{uv} \gt 0 \end{cases}
$$
最大流基本方法(Ford-Fulkerson)
- 通过模拟单纯形法,我们得到了一个解决最大流问题的直接算法(Ford-Fulkerson)。该算法采取迭代的方式进行,每次先构造一个 $G^f$,然后在 $G^f$ 中寻找 s 到 t 的一条可行的增广(能够继续提高流量的)路径,找不到任何这样的路径时算法停止。
- Ford-Fulkerson 方法
- Ford-Fulkerson 方法,即增广路方法,是一种迭代的方法,之所以称之为方法,而不是算法,因为FF(Ford-Fulkerson) 包含不同运行时间的几种实现。
- Ford-Fulkerson 方法伪代码如下,解决了以下三个子问题:①while:要增广多少次?②augmenting path:如何找到一条增广路径?③update:如何增广?
1
2
3
4
5
6FORD-FULKERSON-METHOD(G, s, t):
initialize flow f to 0
while there exists an augmenting path p, path-flow as its remaining capacity
do augment flow path-flow along p to flow f
update residual graph
return flow f
- 最大流算法 Ford-Fulkerson 方法最优性验证
- 最大流最小割定理:设 $f$ 为流网络 $G = (V, E)$ 中的一个流,该流网络的源点为 s,汇点为t,则下面的条件是等价的:
- $f$ 是 $G$ 的一个最大流
- 残量网络 $G^f$ 不包含任何增广路径
- $|f| = |C(S, T)|$,即最大流流量等于割 $C$ 的容量,割 $C=(S, T)$ 是流网络 $G$ 的最小割
- 找到最大流 $f$ $\Longrightarrow$ 残量网络 $G^f$ 中已经无法找到任何由 s 到 t 的路径 $\Longrightarrow$ $(L, R)$ 为图 $G$ 的一个分割 $\begin{cases} L为 G^f 中 s 可达的所有节点集合 \cr R=V-L 为剩余的节点 \end{cases}$
- 对于任意流 $f$ 和任意 $(s, t)$ 分割 $(L, R)$,$流量(f) \leq 容量(L, R)$,由最大流最小割定理,最大流算法产生最小割,最小割对应于流的上限,这就是所求得流的最优性的保证。
- 最大流最小割定理:设 $f$ 为流网络 $G = (V, E)$ 中的一个流,该流网络的源点为 s,汇点为t,则下面的条件是等价的:
- 最大流算法的运行效率
- FORD-FULKERSON-METHOD 每个单次循环都是效率很高的,无论通过使用 DFS 还是 BFS,每次循环都只需要 $O(|E|)$ 的时间,但问题是,我们一共需要循环多少次呢?可以看出,循环次数的上线是所有边流量的最大值 C(每次循环只能增加 1 个流量),算法最坏情况为 $O(C|E|)$,然而 C 可能是一个很大的值!
- 采用广度优先搜索将使得找到的增广路径包含最少的边,则不管边的容量如何,C 如何,最终的迭代次数将不超过 $O(|V|·|E|)$(所有可能的路径总和)。因此,通过仔细地选择增广路径,可以将循环次数限制在 $O(|V|·|E|)$ 之内,在这种情况下,整个算法的时间复杂度为 $O(|V|·|E|^2)$。在 FORD-FULKERSON-METHOD 中通过 BFS 搜索增广路径,这就是Edmonds-Karp 算法(最短路径增广算法),其算法实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231// MaxFlow.cpp
using namespace std;
struct adjVertexNode {
int adjVertexIdx;
int capacity;
adjVertexNode* next;
};
// Alignment-requirement: the first char is expanded to 4(8) bytes in 32-bit(64-bit) machine
// sizeof(VertexNode) == 16(32)
struct VertexNode {
char data;
int vertexIdx;
adjVertexNode* list;
};
struct Graph {
VertexNode VertexNodes[MAX_VERTEX_NUM];
int vertexNum;
int edgeNum;
};
void CreateGraph (Graph& g) {
int i, j, edgeStart, edgeEnd, capacity;
adjVertexNode* adjNode;
//cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
cin >> g.vertexNum >> g.edgeNum;
//cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
for (i=0; i<g.vertexNum; i++) {
cin >> g.VertexNodes[i].data; // vertex data info.
g.VertexNodes[i].vertexIdx = i;
g.VertexNodes[i].list = NULL;
}
//cout << "input edge information(start end):" << endl;
for (j=0; j<g.edgeNum; j++) {
cin >> edgeStart >> edgeEnd >> capacity;
// insert new adjacent VertexNode at the begining of the adjacent list
adjNode = new adjVertexNode;
adjNode->adjVertexIdx = edgeEnd;
adjNode->capacity = capacity;
adjNode->next = g.VertexNodes[edgeStart].list;
g.VertexNodes[edgeStart].list = adjNode;
}
}
void PrintAdjList(const Graph& g) {
cout << "The adjacent list for graph is:" << endl;
for (int i=0; i < g.vertexNum; i++) {
cout << " " << g.VertexNodes[i].data << "->";
adjVertexNode* head = g.VertexNodes[i].list;
if (head == NULL)
cout << "NULL";
while (head != NULL) {
cout << g.VertexNodes[head->adjVertexIdx].data
<< "(" << head->capacity << ")" << " ";
head = head->next;
}
cout << endl;
}
}
void PrintPath(const Graph& g, int* prevs, int toIdx) {
// no previous node ==> reach starting node
if (prevs[toIdx] != -1) {
PrintPath(g, prevs, prevs[toIdx]);
cout << "->";
}
cout << g.VertexNodes[toIdx].data;
}
void DeleteGraph(Graph& g) {
for (int i=0; i<g.vertexNum; i++) {
adjVertexNode* tmp = NULL;
while(g.VertexNodes[i].list != NULL) {
tmp = g.VertexNodes[i].list;
g.VertexNodes[i].list = g.VertexNodes[i].list->next;
delete tmp;
tmp = NULL;
}
}
}
bool BFS(int** graph, int vertexNum, int fromIdx, int toIdx, int* prevs) {
// cout << "BFS" << endl;
// for(int u=0; u<vertexNum; u++) {
// for(int v=0; v<vertexNum; v++) {
// if(graph[u][v] > 0) {
// cout << u << "->" << v << "(" << graph[u][v] << ") ";
// }
// }
// cout << endl;
// }
bool visited[vertexNum];
for(int vertexIdx=0; vertexIdx<vertexNum; vertexIdx++) {
visited[vertexIdx] = false;
prevs[vertexIdx] = -1;
}
queue<int> vertexIdxQueue;
vertexIdxQueue.push(fromIdx);
visited[fromIdx] = true;
while (!vertexIdxQueue.empty()) {
int u = vertexIdxQueue.front();
// cout << u << " ";
if(u == toIdx) {
break;
}
vertexIdxQueue.pop();
for(int v=0; v<vertexNum; v++) {
if(!visited[v] && graph[u][v] > 0) {
vertexIdxQueue.push(v);
visited[v] = true;
prevs[v] = u;
}
}
}
return visited[toIdx];
}
int FordFulkerson(const Graph& g, const VertexNode& source, const VertexNode& sink) {
int maxFlow = 0;
int flowGraph[g.vertexNum][g.vertexNum];
// initialize the residual graph
int** residualGraph = new int*[g.vertexNum];
for(int u=0; u<g.vertexNum; u++) {
residualGraph[u] = new int[g.vertexNum];
for(int v=0; v<g.vertexNum; v++) {
residualGraph[u][v] = 0;
flowGraph[u][v] = 0;
}
}
for(int vertexIdx=0; vertexIdx<g.vertexNum; vertexIdx++) {
adjVertexNode* head = g.VertexNodes[vertexIdx].list;
while (head != NULL) {
// cout << vertexIdx << "-->" << head->adjVertexIdx << endl;
residualGraph[vertexIdx][head->adjVertexIdx] = head->capacity;
head = head->next;
}
}
// prevs array for storing the augmenting path
int prevs[g.vertexNum];
int iter = 1;
cout << " Maximum Flow Algorithm Process:" << endl;
// Augment the flow while there is a path from source to sink
while(BFS(residualGraph, g.vertexNum, source.vertexIdx, sink.vertexIdx, prevs)) {
// find the maximum flow(minimum residual capacity) through the path found
int pathFlow = INT_MAX;
for(int v=sink.vertexIdx; v!=source.vertexIdx; v=prevs[v]) {
int u = prevs[v];
if(residualGraph[u][v] < pathFlow) {
pathFlow = residualGraph[u][v];
}
}
// update residual capacities of the edges & reverse edges along the augmenting path
for(int v=sink.vertexIdx; v!=source.vertexIdx; v=prevs[v]) {
int u = prevs[v];
residualGraph[u][v] -= pathFlow;
residualGraph[v][u] += pathFlow;
// record flows
flowGraph[u][v] += pathFlow;
}
maxFlow += pathFlow;
// print current iteration's info
cout << "\t#" << iter++ << " flow: " << setw(3) << pathFlow << " Augmenting-path: ";
PrintPath(g, prevs, sink.vertexIdx);
cout << endl;
}
// memory release
for(int i=0; i<g.vertexNum; i++) {
delete[] residualGraph[i];
}
delete[] residualGraph;
// show the flows
cout << " Maximum Flow Graph:" << endl;
bool noflow;
for(int u=0; u<g.vertexNum; u++) {
noflow = true;
cout << " " << g.VertexNodes[u].data << ": ";
for(int v=0; v<g.vertexNum; v++) {
if(flowGraph[u][v] > 0) {
cout << "->" << g.VertexNodes[v].data
<< "(" << flowGraph[u][v] << ")\t";
noflow = false;
}
}
if(noflow) {
cout << "NULL";
}
cout << endl;
}
return maxFlow;
}
int main(int argc, const char** argv) {
freopen("flow1.txt", "r", stdin);
freopen("flow2.txt", "r", stdin);
Graph g;
CreateGraph(g);
PrintAdjList(g);
cout << endl;
cout << " Maximum Flow: " << FordFulkerson(g, g.VertexNodes[0], g.VertexNodes[6]) << endl;
cout << " Maximum Flow: " << FordFulkerson(g, g.VertexNodes[0], g.VertexNodes[5]) << endl;
DeleteGraph(g);
return 0;
}
- 算法实现细节分析如下:
bool BFS(int** graph, int vertexNum, int fromIdx, int toIdx, int* prevs)函数通过广度优先搜索算法寻找边数目最少的增广路径,返回值表示能否寻找到这样的一条路径;假如存在这样的一条增广路径,prevs数组则记录这样的一条增广路径:toIdx → prevs[toIdx] → prevs[prevs[toIdx]] → … → fromIdx。residualGraph[u][v]通过邻接矩阵的方式维护一个残量网络,flowGraph则维护了流量网络的情况。pathFlow则用于获取每次迭代寻找到的该增广路径的残存容量,用于更新残量网络和流量网络。maxFlow则保留了最终的最大流量值。
- 算法运行实例(一)
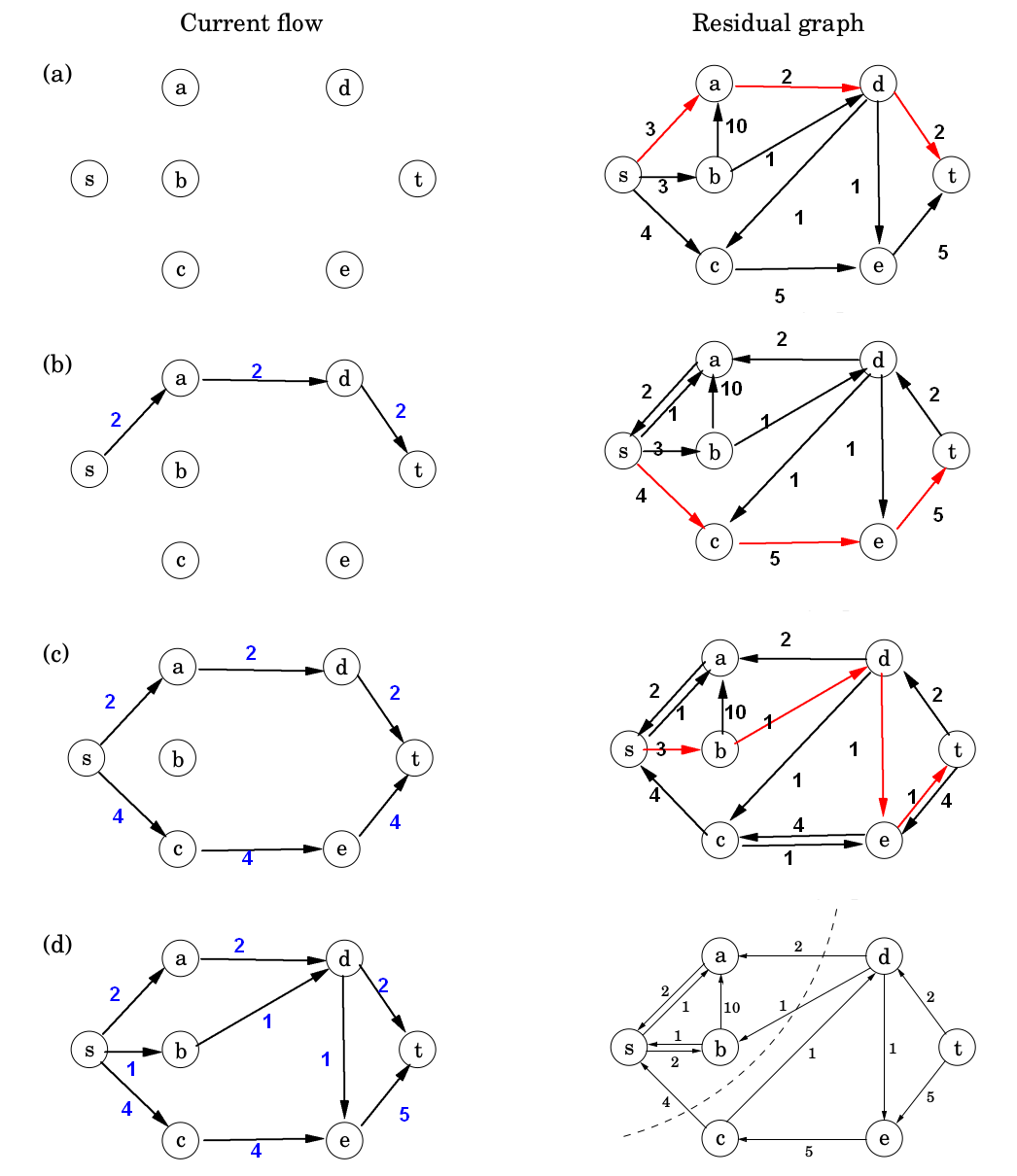
- 上图网络流对应的输入文件 flow1.txt 如下:
-
1
2
3
4
5
6
7
8
9
10
11
12
137 11
s a b c d e t
0 1 3
0 2 3
0 3 4
1 4 2
2 1 10
2 4 1
3 5 5
4 3 1
4 5 1
4 6 2
5 6 5- 编译构建,运行结果如下,过程可视化如上图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24g++ -DUSE_FLOW1 MaxFlow.cpp -o MaxFlow
./MaxFlow
The adjacent list for graph is:
c(4) b(3) a(3)
d(2)
d(1) a(10)
e(5)
t(2) e(1) c(1)
t(5)
NULL
Maximum Flow Algorithm Process:
1 flow: 2 Augmenting-path: s->a->d->t
2 flow: 4 Augmenting-path: s->c->e->t
3 flow: 1 Augmenting-path: s->b->d->e->t
Maximum Flow Graph:
s: ->a(2) ->b(1) ->c(4)
a: ->d(2)
b: ->d(1)
c: ->e(4)
d: ->e(1) ->t(2)
e: ->t(5)
t: NULL
Maximum Flow: 7
- 编译构建,运行结果如下,过程可视化如上图。
- 算法运行实例(二)
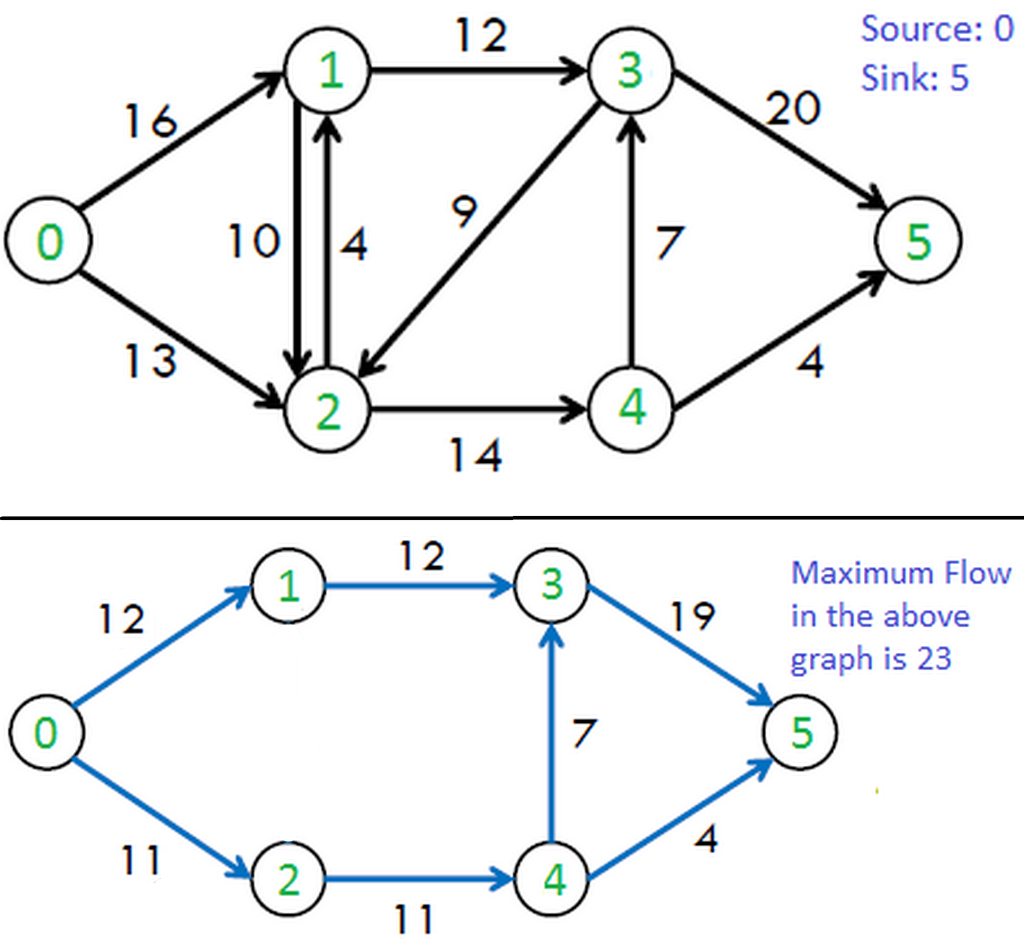
- 上图网络流对应的输入文件 flow2.txt 如下:
-
1
2
3
4
5
6
7
8
9
10
11
126 10
0 1 2 3 4 5
0 1 16
0 2 13
1 2 10
1 3 12
2 1 4
2 4 14
3 2 9
3 5 20
4 3 7
4 5 4- 编译构建,运行结果如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22g++ MaxFlow.cpp -o MaxFlow
./MaxFlow
The adjacent list for graph is:
2(13) 1(16)
3(12) 2(10)
4(14) 1(4)
5(20) 2(9)
5(4) 3(7)
NULL
Maximum Flow Algorithm Process:
1 flow: 12 Augmenting-path: 0->1->3->5
2 flow: 4 Augmenting-path: 0->2->4->5
3 flow: 7 Augmenting-path: 0->2->4->3->5
Maximum Flow Graph:
0: ->1(12) ->2(11)
1: ->3(12)
2: ->4(11)
3: ->5(19)
4: ->3(7) ->5(4)
5: NULL
Maximum Flow: 23
- 编译构建,运行结果如下:
References
- 基本概念:
- 网络流:最大流,最小割 基本概念及算法
- 图的匹配问题与最大流问题(一)
- 最大流问题跟线性规划又是如何产生联系的呢?
- 算法涉及概念补充:最大流, 最小割问题及算法实现
- 算法实现细节: