2017-06-01

算法设计与分析[0016] 二分图匹配问题

二分图匹配问题

二分图
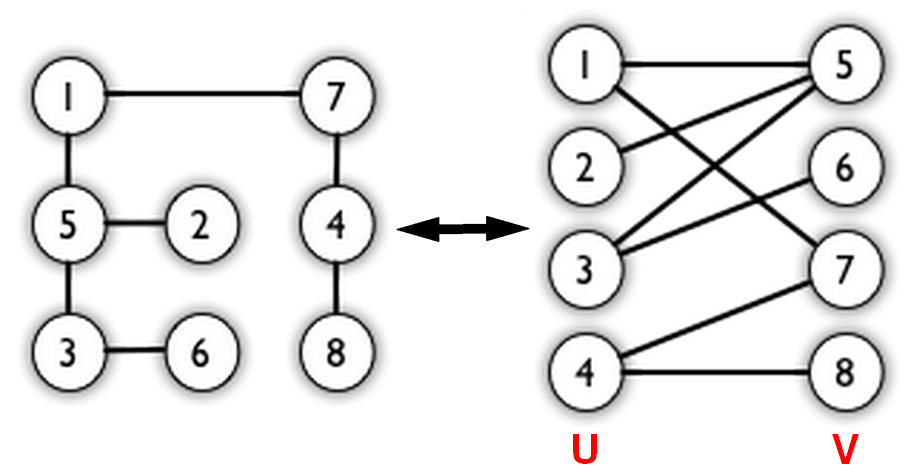
- 顶点被分成两个不相交的集合（$U$ 和 $V$）并且同属一个集合内的点两两不相连（$E_{in U} = E_{in V} = \emptyset$），即要么没有圈，要么圈所包含的边数必定是偶数。
- 二分图 的一个等价定义是：不含有 含奇数条边的环 的图。
匹配是边的集合 $M$（$M \subseteq E$），其中任意的两条边不共点：$e_1, e_2 \in M, e_1 \cap e_2 = \varnothing $
- 集合 $M$ 中的元素（边），称为 匹配边
- 匹配边所连接的点被称为 匹配点
- 同理可以定义 非匹配边 和 非匹配点 的概念
最大匹配
- 对于一个二分图可能有多种匹配，如果二分图里的某一个匹配包含的边的数量，在该二分图的所有匹配中最大，那么这个匹配称为 最大匹配
- 如果一个图的某个匹配中，所有的顶点都是匹配点（可能会残留一些边不是匹配边），那么它就是一个 完美匹配。
- 显然，完美匹配 一定是 最大匹配（完美匹配 的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）；但并非每个图都存在 完美匹配，即 最大匹配 不一定是 完美匹配。
增广路径（增广轨）
- 在二分图的匹配中，如果一条路径的首尾是 非匹配点，路径中除此之外的（如果有）其他点均是 匹配点，那么这条路径就是一条 增广路径（agumenting path）/增广轨（顾名思义是指一条可以使匹配数变多的路径）。
  - $A：$首尾是非匹配点，因此，增广路径的第一条和最后一条边，必然是 非匹配边。
  - $B：$增广路径的第二条（如果有）和倒数第二条（如果有），必然是 匹配边 $\Longleftarrow N$ 个点（$0～N-1$），$v_1, v_2, …, v_{N-3}, v_{N-2}$ 均为匹配点，且 ($v_0 → v_1$) 和 ($v_{N-2} → v_{N-1}$) 为 非匹配边。
  - $C：$第三条（如果有）和倒数第三条（如果有）一定是 非匹配边 $\Longleftarrow $($v_1 → v_2$)$\in M$，($v_1 → v_2$)$\cap$($v_2 → v_3$)$= v_2$，故 ($v_2 → v_3$) 只能是 非匹配边
- $A, B, C \Longrightarrow$ 增广路径从非匹配边开始，匹配边和非匹配边依次交替，最后由非匹配边结束 $\Longrightarrow$ 增广路径中，非匹配边的数目会比匹配边大 1。
- 在二分图的匹配中，从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫 交替路径/交替轨。
  - 增广路径/增广轨 也被称为 交替路径/交替轨。

判断一个图是否为二分图？

假设我们有一个图，我们尝试用如下的方式去给每个节点着色，总共所有的节点只能着两种颜色中的一种（假设为红色或者蓝色）。对于一个节点来说，假设它着的是某一种颜色，和它相邻的节点只能着另一种颜色。给定一个图，如果这个图满足上述的特性的话，则这个图可以称之为二分图。
- 判断一个图是否为二分图必然会遍历这个图
- 每次在判断的时候假定一个节点的颜色为某个值，那么再将它相邻的节点颜色都设置成不同的。因为只是两种颜色，可以直接用布尔值类型来处理。
  - 对于不属于二分图的情况，肯定是某个节点访问到一个它可以连接到的节点，而这个节点已经被访问过了，但是这个被访问过的节点和当前节点颜色是一样。这样表明它和前面二分图的定义有冲突，所以，我们遍历整个图就是为了判断是否存在这种情况。
实际实现中需要考虑的细节。
- 对于所有节点对应的颜色需要定义一个boolean[] color数组
- 最开始访问一个节点的时候，将其对应color位设置为true，每次访问一个关联的节点时，将关联节点设置成原来节点的相反值。也就是说，比如节点$v$它的颜色为color[v]，那么下一个它被关联的节点$w$的颜色则可以设置成color[w] = !color[v]，正好通过取反实现了颜色的变换。
- 这里实现的要点还是通过dfs方法
  - 每次碰到一个节点的时候就要判断一下是否已经访问过：①已经访问过的话，要判断颜色是否相同，相同则表明该图不是一个二分图；②没有访问过的话，则将新节点设置成当前节点的相反值。
  - 然后就是要遍历所有节点，防止遗漏未连接的节点情况。

bool[] color;
visited[] = false;
 
for 所有节点 ?:
  if(!visited[?])
    color[?] = true;
    if(!dfs(?, visited, color))
      // 不是二分图
// 为二分图
 
bool dfs(startIdx, visited, color) {
  visited[startIdx] = true;
  for startIdx 邻接边 startIdx->?:
    if(!visited[?]){
      color[?] = !color[startIdx];
      if(!dfs(?, visited, color))
        return false;
    }
    else if(color[startIdx] == color[?]) {
      return false;
    }
  return true;
}

可以看出，一个图是不是二分图并不严格要求其必须是一个连通图。

匈牙利算法

增广路径的性质
- 有奇数条边
- 起点在二分图的左半边$U$，终点在右半边$V$
- 路径上的点一定是一个在左半边，一个在右半边，交替出现。（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连）
- 整条路径上没有重复的点
- 起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的
- 路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中
- 最后，也是最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个
算法思想
- 初始时最大匹配为空。
- 从二分图中找出一条路径来，让路径的起点和终点都是还没有匹配过的点，并且路径经过的连线是一条没被匹配、一条已经匹配过、再下一条又没被匹配过这样交替的出现。
- 找到这样的路径后，显然路径里没被匹配过的连线比已经匹配了的连线多一条，于是修改匹配图，把路径里所有匹配过的连线去掉匹配关系，把没有匹配的连线变成匹配的，这样匹配数就比原来多1。
- 不断执行上述操作，直到找不到这样的路径为止。
  - 从反证法考虑，即假设存在这样的情况：当前匹配不是二分图的最大匹配，但已找不到一条新的增广路径。因为当前匹配不是二分图的最大匹配，那么在两个集合中，分别至少存在一个非匹配点。那么情况分为两种：
    - 这两个点之间存在一条边——那么我们找到了一条新的增广路径，产生矛盾；
    - 这两个点之间不存在直接的边，即这两个点分别都只与匹配点相连——那么：（1）如果这两个点可以用已有的匹配点相连，那么我们找到了一条新的增广路径，产生矛盾；（2）如果这两个点无法用已有的匹配点相连，那么这两个点也就无法增加匹配中边的数量，也就是我们已经找到了二分图的最大匹配，产生矛盾。
  - 在所有可能的情况，上述假设都会产生矛盾。因此假设不成立，亦即贪心算法：不断地搜寻出增广路径，直到最终我们找不到新的增广路径为止，必然能求得最大匹配的解。
- 如果二分图的左半边 $U$ 一共有 $|V_U|$ 个点，最多找 $|V_U|$ 条增广路径，如果图中有 $|E|$ 条边，每一条增广路径把所有边遍历一遍，所以时间复杂度为 $O(|V_U|·|E|)$。

BigraphMatching.cpp

#include <iostream>
#include <stdio.h>		/* stdin */
#include <limits.h>		/* INT_MAX */
#include <queue>		/* queue */
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
#define UNMATCHING 	-1
#define STARTPOINT	-1
  
struct adjVertexNode {
  int adjVertexIdx;
  adjVertexNode* next;
};
 
struct VertexNode {
  char data;
  int vertexIdx;
  // 0: in U/ 1: in V
  int UorV;
  adjVertexNode* list;
};
  
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
  
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd;
  // 0: in U/1: in V
  int UorV;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data >> UorV; // vertex data info.
    g.VertexNodes[i].vertexIdx = i;
    g.VertexNodes[i].UorV = UorV;
    g.VertexNodes[i].list = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
    // Bigraph is a undirected graph
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeStart;
    adjNode->next = g.VertexNodes[edgeEnd].list;
    g.VertexNodes[edgeEnd].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for Bigraph<U, V> is:" << endl;
 
  for (int i=0; i<g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data;
    cout << "(";
    if(g.VertexNodes[i].UorV == 0) {
      cout << "U";
    }
    else {
      cout << "V";
    }
    cout << ")->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << " ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
void PrintPath(const Graph& g, int prevs[], int toIdx) {
  if (prevs[toIdx] != STARTPOINT) {
    PrintPath(g, prevs, prevs[toIdx]);
    cout << "->";
  }
  cout << g.VertexNodes[toIdx].data;
}
  
void PrintMatching(Graph& g, const int matchings[]) {
  bool visited[g.vertexNum] = {false};
  for(int i=0; i<g.vertexNum; i++) {
    if(matchings[i]!=-1 && !visited[i]) {
      cout << "\t+ "
         << g.VertexNodes[i].data << "<-->" << g.VertexNodes[matchings[i]].data
         << endl;
     	visited[i] = true;
     	visited[matchings[i]] = true;
    }
  }
  cout << endl;
}
 
int Hungarian(Graph& g, int matchings[]) {
  int U[g.vertexNum], V[g.vertexNum];
  int uSize = 0, vSize = 0;
  for(int vertex=0; vertex<g.vertexNum; vertex++) {
    if(g.VertexNodes[vertex].UorV == 0) {
      U[uSize++] = g.VertexNodes[vertex].vertexIdx;
    }
    else {
      V[vSize++] = g.VertexNodes[vertex].vertexIdx;
    }
  }
 
  int matchingSize = 0;
  for(int i=0; i<g.vertexNum; i++) {
    // -1 means no matching
    matchings[i] = UNMATCHING;
  }
  // cout << "U: #" << uSize << " V: #" << vSize << endl;
 
  int prevs[g.vertexNum];
  queue<int> bfsVertexQueue;
 
  cout << endl << "Hungarian Algorithm's Process: " << endl;
  for(int vertexInU=0; vertexInU<uSize; vertexInU++) {
    int vertexIdx = U[vertexInU];
    cout << "\t" << g.VertexNodes[vertexIdx].data << ": ";
    // find an agumenting path, starting with an unmatching vertex
    if(matchings[vertexIdx] == UNMATCHING) {
      cout << "unmatched vertex" << endl;
 
      while(!bfsVertexQueue.empty()) {
        bfsVertexQueue.pop();
      }
      bool visited[g.vertexNum] = {false};
 
      bfsVertexQueue.push(vertexIdx);
      visited[vertexIdx] = true;
      // prevs for augumenting path's backtracking, -1 means starting point
      prevs[vertexIdx] = STARTPOINT;
 
      bool pathFound = false;
      while(!bfsVertexQueue.empty() && !pathFound) {
        int u = bfsVertexQueue.front();
        // cout << "pop: " << g.VertexNodes[u].data << endl;
        bfsVertexQueue.pop();
 
        adjVertexNode* head = g.VertexNodes[u].list;
        while (head != NULL && !pathFound) {
          int v = head->adjVertexIdx;
          // visited: avoid loop
          if(!visited[v]) {
            // v is a matching vertex
            if(matchings[v] != UNMATCHING) {
              bfsVertexQueue.push(matchings[v]);
              visited[v] = true;
              visited[matchings[v]] = true;
              prevs[v] = u;
              prevs[matchings[v]] = v;
              // cout << "push: " << g.VertexNodes[matchings[v]].data << endl;
            }
            // v is the other unmatching vertex, augumenting path found
            else {
              // record previous vertex for backtracking
              prevs[v] = u;
 
              pathFound = true;
              cout << "\t\tAugumenting path: ";
              PrintPath(g, prevs, v);
              cout << endl;
 
              // reverse the augumenting path, for one more matching
              int curIdx = v, prevIdx = u;
              bool isMatchedEdge = false;
              while(prevIdx != STARTPOINT) {
                if(!isMatchedEdge) {
                  matchings[curIdx] = prevIdx;
                  matchings[prevIdx] = curIdx;
                }
                isMatchedEdge = !isMatchedEdge;
                curIdx = prevIdx;
                prevIdx = prevs[prevIdx];
              }
            }
          }
          
          head = head->next;
        }
      }
      // expand one more matching
      if(matchings[vertexIdx] != UNMATCHING) {
        matchingSize++;
      }
    }
    else {
      cout << "matched vertex" << endl;
    }
  }
 
  return matchingSize;
}
 
int main(int argc, const char** argv) {
  #ifdef USE_GRAPH1
    freopen("Bigraph1.txt", "r", stdin);
  #else
    freopen("Bigraph2.txt", "r", stdin);
  #endif
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);

  int matchings[g.vertexNum];
  int matchingSize = Hungarian(g, matchings);
 
  cout << endl;
  cout << "Maximum Matching: #" << matchingSize << endl;
  PrintMatching(g, matchings);
   
  DeleteGraph(g);
  return 0;
}

代码实现细节如下
- int Hungarian(Graph& g, int matchings[]) 函数根据传入的二分图 g，运行匈牙利算法确定该二分图的最大匹配数并返回，对应的匹配信息通过 matchings 数组返回。
- 从左边 $U$ 顶点集第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路径。
  - 上述实现中采用BFS进行搜索，也可以采用DFS进行搜索。
    - 如果经过一个未匹配点，说明搜索成功：根据增广路径更新匹配信息，最大匹配数 +1，停止搜索。
    - 如果经过一个匹配点，
  - 如果未能找到增广路径，则跳过这个点进行下一次搜索：事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。
- 由于找到增广路径之后需要沿着路径更新匹配信息（取反操作），所以我们需要一个结构来记录路径上的点。DFS 通过函数递归调用隐式地使用一个栈，而我们的 BFS 实现中使用 prevs 数组来记录增广路径上途径的点信息。
  - 沿着增广路径更新匹配信息（取反操作）是根据增广路径上的匹配边、非匹配边交替出现的性质。
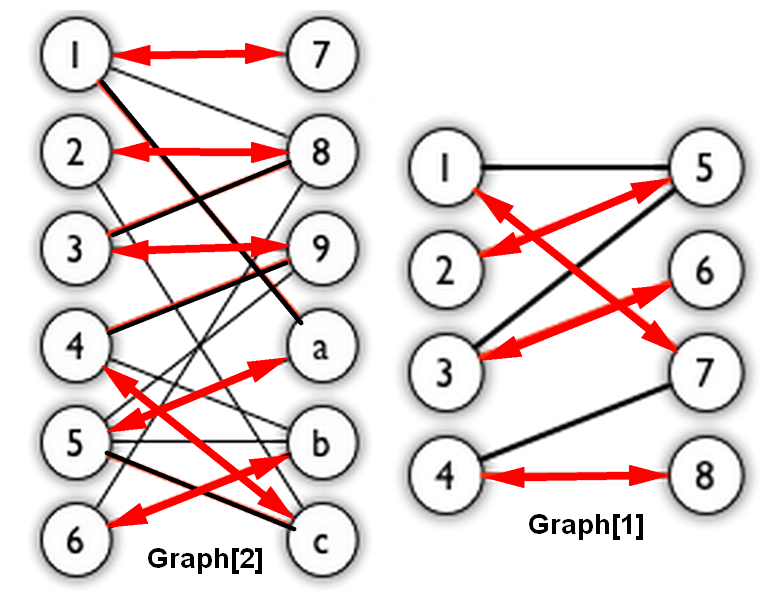
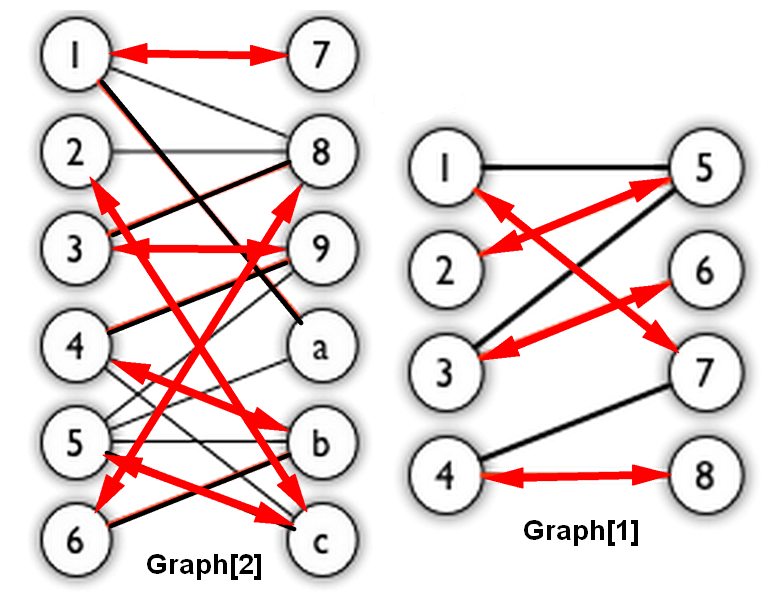
Graph[1] 输入文件如下：

Bigraph1.txt

构建运行结果如下：

$ g++ -DUSE_GRAPH1 BigraphMatching.cpp -o BigraphMatching
$ ./BigraphMatching 
The adjacent list for Bigraph<U, V> is:
 1(U)->7 5 
 2(U)->5 
 3(U)->6 5 
 4(U)->8 7 
 5(V)->3 2 1 
 6(V)->3 
 7(V)->4 1 
 8(V)->4 
 
Hungarian Algorithm's Process: 
  1: unmatched vertex
    Augumenting path: 1->7
  2: unmatched vertex
    Augumenting path: 2->5
  3: unmatched vertex
    Augumenting path: 3->6
  4: unmatched vertex
    Augumenting path: 4->8
 
Maximum Matching: #4
  + 1<-->7
  + 2<-->5
  + 3<-->6
  + 4<-->8

Graph[2] 输入文件如下：

Bigraph2.txt

构建运行结果如下：

$ g++ BigraphMatching.cpp -o BigraphMatching
$ ./BigraphMatching 
The adjacent list for Bigraph<U, V> is:
 1(U)->a 8 7 
 2(U)->c 8 
 3(U)->9 8 
 4(U)->c b 9 
 5(U)->c b a 9 
 6(U)->b 8 
 7(V)->1 
 8(V)->6 3 2 1 
 9(V)->5 4 3 
 a(V)->5 1 
 b(V)->6 5 4 
 c(V)->5 4 2 
 
Hungarian Algorithm's Process: 
  1: unmatched vertex
    Augumenting path: 1->a
  2: unmatched vertex
    Augumenting path: 2->c
  3: unmatched vertex
    Augumenting path: 3->9
  4: unmatched vertex
    Augumenting path: 4->b
  5: unmatched vertex
    Augumenting path: 5->c->2->8
  6: unmatched vertex
    Augumenting path: 6->b->4->c->5->a->1->7
 
Maximum Matching: #6
  + 1<-->7
  + 2<-->8
  + 3<-->9
  + 4<-->c
  + 5<-->a
  + 6<-->b

补充概念：匈牙利树
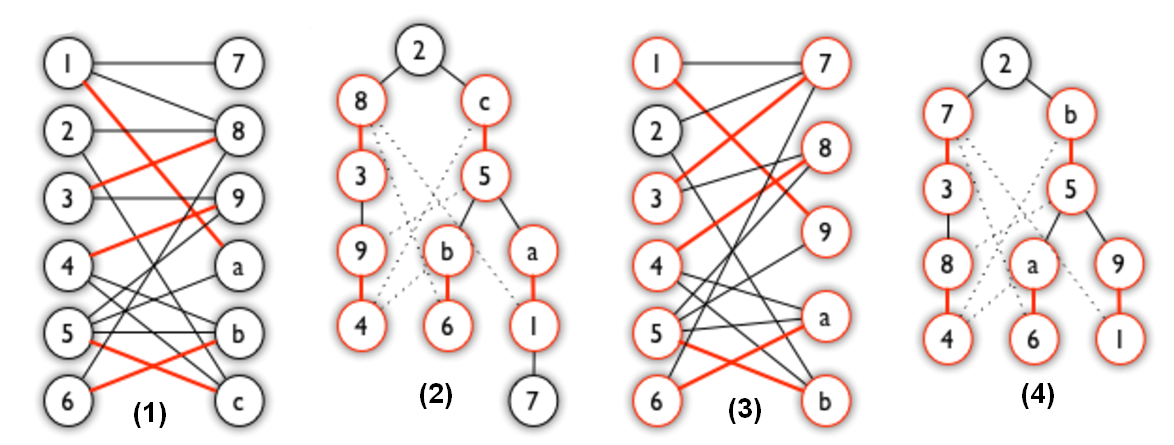
- 上文提到的 匈牙利树 一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。
- 上图（1），可以得到如图（2）的一棵 BFS 树：这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。相比之下，由图（3）得到的如图（4）的一棵 BFS 树，就是一棵匈牙利树。

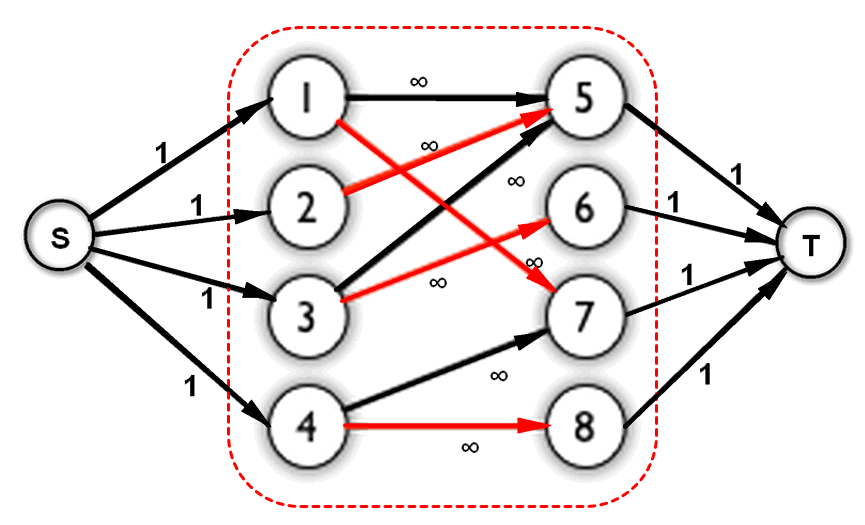
最大流方法计算最大匹配

　如下图所示，对于一个二分图$G$，令已有的边的容量（Capacity）为无穷大，增加一个源点$S$和一个汇点$T$，令$S$和$T$分别连接二分图中的左半边$U$和右半边$V$，并设置其容量为1。这时得到流网络$G’$，计算得到的$G’$最大流就等于$G$的最大匹配。

算法正确性简单证明
- 首先假设，当前流网络有一个最大流，但它对应的不是最大匹配。那么，我们至少还可以向最大匹配中加入一条边$(u→v)$，显然我们还可以增加一条增广路径：s->u->v->t，那么就得到一个更大的流，和假设矛盾，所以假设不成立。
- 同理，假设当前有一个最大匹配，其对应的不是最大流，那么至少还存在一条增广路径s->u->v->t以确保更大的流，这时就可以增加边$(u→v)$到最大匹配中，同样和假设矛盾。

BigraphMatchingbyMaxFlow.cpp

#include <iostream>
#include <iomanip>			/* setw */ 
#include <stdio.h>			/* stdin */
#include <limits.h>			/* INT_MAX */
#include <queue>			/* queue */
 
using namespace std;
  
#define MAX_VERTEX_NUM    26
 
#define UNMATCHING 	-1
#define STARTPOINT	-1
 
struct adjVertexNode {
  int adjVertexIdx;
  adjVertexNode* next;
};
 
struct VertexNode {
  char data;
  int vertexIdx;
  // 0: in U/ 1: in V
  int UorV;
  adjVertexNode* list;
};
 
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
 
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd;
  // 0: in U/1: in V
  int UorV;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data >> UorV; // vertex data info.
    g.VertexNodes[i].vertexIdx = i;
    g.VertexNodes[i].UorV = UorV;
    g.VertexNodes[i].list = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd;
    
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
    // Bigraph is a undirected graph
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeStart;
    adjNode->next = g.VertexNodes[edgeEnd].list;
    g.VertexNodes[edgeEnd].list = adjNode;
  }
}
 
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for Bigraph<U, V> is:" << endl;
  
  for (int i=0; i<g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data;
    cout << "(";
    if(g.VertexNodes[i].UorV == 0) {
      cout << "U";
    }
    else {
      cout << "V";
    }
    cout << ")->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << " ";
      head = head->next;
    }
    cout << endl;
  }
}
 
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
 
void PrintPath(const Graph& g, int prevs[], int toIdx) {
  if (prevs[toIdx] != STARTPOINT) {
    PrintPath(g, prevs, prevs[toIdx]);
    cout << "->";
  }
  if(toIdx == 0) {
    cout << "S";
  }
  else if(toIdx == g.vertexNum+1) {
    cout << "T";
  }
  else {
    cout << g.VertexNodes[toIdx-1].data;
  }
}
 
void PrintMatching(Graph& g, const int matchings[]) {
  bool visited[g.vertexNum] = {false};
  for(int i=0; i<g.vertexNum; i++) {
    if(matchings[i]!=-1 && !visited[i]) {
      cout << "\t+ "
         << g.VertexNodes[i].data << "<-->" << g.VertexNodes[matchings[i]].data
         << endl;
     	visited[i] = true;
     	visited[matchings[i]] = true;
    }
  }
  cout << endl;
}
 
bool BFS(int** graph, int vertexNum, int fromIdx, int toIdx, int* prevs) {
  bool visited[vertexNum];
  for(int vertexIdx=0; vertexIdx<vertexNum; vertexIdx++) {
    visited[vertexIdx] = false;
    prevs[vertexIdx] = -1;
  }
 
  queue<int> vertexIdxQueue;
  vertexIdxQueue.push(fromIdx);
  visited[fromIdx] = true;
  while (!vertexIdxQueue.empty()) {
    int u = vertexIdxQueue.front();
    // cout << u << " ";
    if(u == toIdx) {
      break;
    }
    vertexIdxQueue.pop();
    
    for(int v=0; v<vertexNum; v++) {
      if(!visited[v] && graph[u][v] > 0) {
        vertexIdxQueue.push(v);
        visited[v] = true;
        prevs[v] = u;
      }
    }
  }
  
  return visited[toIdx];
}
 
int MaxMatchingbyMaxFlow(Graph& g, int matchings[]) {
  for(int i=0; i<g.vertexNum; i++) {
    matchings[i] = UNMATCHING;
  }
 
  // Add source[0] and sink[g.vertexNum+1]
  int N = g.vertexNum+2;
  int sourceIdx = 0, sinkIdx = g.vertexNum+1;
 
  int maxFlow = 0;
  int flowGraph[N][N];
  // initialize the residual graph
  int** residualGraph = new int*[N];
  for(int u=0; u<N; u++) {
    residualGraph[u] = new int[N];
    for(int v=0; v<N; v++) {
      residualGraph[u][v] = 0;
      flowGraph[u][v] = 0;
    }
  }
 
  for(int vertexIdx=0; vertexIdx<g.vertexNum; vertexIdx++) {
    if(g.VertexNodes[vertexIdx].UorV == 0) {
      residualGraph[sourceIdx][vertexIdx+1] = 1;
 
      adjVertexNode* head = g.VertexNodes[vertexIdx].list;
      while (head != NULL) {
        residualGraph[vertexIdx+1][head->adjVertexIdx+1] = INT_MAX;
        head = head->next;
      }
    }
    else {
      residualGraph[vertexIdx+1][sinkIdx] = 1;
    }
  }
 
  // prevs array for storing the augmenting path
  int prevs[N];
  int iter = 1;
 
  cout << " Maximum Flow Algorithm Process:" << endl;
  // Augment the flow while there is a path from source to sink
  while(BFS(residualGraph, N, sourceIdx, sinkIdx, prevs)) {
    // find the maximum flow(minimum residual capacity) through the path found
    int pathFlow = INT_MAX;
    for(int v=sinkIdx; v!=sourceIdx; v=prevs[v]) {
      int u = prevs[v];
      if(residualGraph[u][v] < pathFlow) {
        pathFlow = residualGraph[u][v];
      }
    }
    // update residual capacities of the edges & reverse edges along the augmenting path
    for(int v=sinkIdx; v!=sourceIdx; v=prevs[v]) {
      int u = prevs[v];
      residualGraph[u][v] -= pathFlow;
      residualGraph[v][u] += pathFlow;
      // record flows
      flowGraph[u][v] += pathFlow;
    }
    // update matching from augumenting path
    int curIdx = prevs[sinkIdx], prevIdx = prevs[curIdx];
    while(prevIdx != STARTPOINT) {
      // -1 with source and sink
      matchings[curIdx-1] = prevIdx-1;
      matchings[prevIdx-1] = curIdx-1;

      curIdx = prevs[prevIdx];
      prevIdx = prevs[curIdx];
    }
 
    maxFlow += pathFlow;
    // print current iteration's info
    cout << "\t#" << iter++ << " flow: " << setw(3) << pathFlow << " Augmenting-path: ";
    PrintPath(g, prevs, sinkIdx);
    cout << endl;
  }
 
  // memory release
  for(int i=0; i<N; i++) {
    delete[] residualGraph[i];
  }
  delete[] residualGraph;
 
  // show the flows
  cout << " Maximum Flow Graph:" << endl;
  bool noflow;
  for(int u=0; u<g.vertexNum; u++) {
    noflow = true;
    cout << "   " << g.VertexNodes[u].data << ": ";
    for(int v=0; v<g.vertexNum; v++) {
      if(flowGraph[u+1][v+1] > 0) {
        cout << "->" << g.VertexNodes[v].data
           << "(" << flowGraph[u+1][v+1] << ")\t";
        noflow = false;
      }
    }
    if(noflow) {
      cout << "NULL";
    }
    cout << endl;
  }
 
  return maxFlow;
}
 
int main(int argc, const char** argv) {
  #ifdef USE_GRAPH1
    freopen("Bigraph1.txt", "r", stdin);
  #else
    freopen("Bigraph2.txt", "r", stdin);
  #endif
 
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
  
  int matchings[g.vertexNum];
  int matchingSize = MaxMatchingbyMaxFlow(g, matchings);
  
  cout << endl;
  cout << "Maximum Matching: #" << matchingSize << endl;
  PrintMatching(g, matchings);
  
  DeleteGraph(g);
  return 0;
}

代码实现细节如下：
- int MaxMatchingbyMaxFlow(Graph& g, int matchings[]) 实现了和匈牙利算法中一样的函数接口，思路很简单，residualGraph 初始化为构造的流网络$G’$，然后调用最大流算法，得到的最大流即为返回的最大匹配数；此外，利用最大流算法每次迭代搜索到的增广路径更新匹配信息matchings。
- 因为二分图上任何匹配数目至多为$|V’| = min(|V_{\in U}|, |V_{\in V}|)$，所以流网络$G’$中最大流的值为$O(|V’|)$，因此，可以在$O(|V’|·|E’|) = O(|V|·|E|)$的时间内找出二分图的最大匹配。
利用上述最大流方法得到的匹配信息和匈牙利算法有些许区别，但可以看出，都能正确得到最大匹配，同时也是完美匹配。

Graph[1]

$ g++ -DUSE_GRAPH1 BigraphMatchingbyMaxFlow.cpp -o BigraphMatchingbyMaxFlow
$ ./BigraphMatchingbyMaxFlow 
The adjacent list for Bigraph<U, V> is:
 1(U)->7 5 
 2(U)->5 
 3(U)->6 5 
 4(U)->8 7 
 5(V)->3 2 1 
 6(V)->3 
 7(V)->4 1 
 8(V)->4 
 Maximum Flow Algorithm Process:
	#1 flow:   1 Augmenting-path: S->1->5->T
	#2 flow:   1 Augmenting-path: S->3->6->T
	#3 flow:   1 Augmenting-path: S->4->7->T
	#4 flow:   1 Augmenting-path: S->2->5->1->7->4->8->T
 Maximum Flow Graph:
   1: ->5(1)	->7(1)	
   2: ->5(1)	
   3: ->6(1)	
   4: ->7(1)	->8(1)	
   5: ->1(1)	
   6: NULL
   7: ->4(1)	
   8: NULL
 
Maximum Matching: #4
  + 1<-->7
  + 2<-->5
  + 3<-->6
  + 4<-->8

Graph[2]

$ g++ BigraphMatchingbyMaxFlow.cpp -o BigraphMatchingbyMaxFlow
$ ./BigraphMatchingbyMaxFlow 
The adjacent list for Bigraph<U, V> is:
 1(U)->a 8 7 
 2(U)->c 8 
 3(U)->9 8 
 4(U)->c b 9 
 5(U)->c b a 9 
 6(U)->b 8 
 7(V)->1 
 8(V)->6 3 2 1 
 9(V)->5 4 3 
 a(V)->5 1 
 b(V)->6 5 4 
 c(V)->5 4 2 
 Maximum Flow Algorithm Process:
	#1 flow:   1 Augmenting-path: S->1->7->T
	#2 flow:   1 Augmenting-path: S->2->8->T
	#3 flow:   1 Augmenting-path: S->3->9->T
	#4 flow:   1 Augmenting-path: S->4->b->T
	#5 flow:   1 Augmenting-path: S->5->a->T
	#6 flow:   1 Augmenting-path: S->6->8->2->c->T
 Maximum Flow Graph:
   1: ->7(1)	
   2: ->8(1)	->c(1)	
   3: ->9(1)	
   4: ->b(1)	
   5: ->a(1)	
   6: ->8(1)	
   7: NULL
   8: ->2(1)	
   9: NULL
   a: NULL
   b: NULL
   c: NULL
  
Maximum Matching: #6
  + 1<-->7
  + 2<-->c
  + 3<-->9
  + 4<-->b
  + 5<-->a
  + 6<-->8

最大匹配与最大边独立集

边独立集即一个边集，满足边集中的任意两边不邻接。
极大边独立集(maximal edge independent set)：本身为边独立集，再加入任何边都不是。
最大边独立集(maximum edge independent set)：边最多的边独立集。
边独立数(edge independent number)：最大边独立集的边数。
边独立集又称匹配(matching)，相应的有极大匹配(maximal matching)，最大匹配(maximum matching)，匹配数(matching number)。

最大匹配与最小路径覆盖

给定有向图$G=(V, E)$，设$P$是$G$的一个简单路（顶点不相交）的集合。如果$V$中每个顶点恰好在$P$的一条路上，则称$P$是$G$的一个路径覆盖。$P$中路径可以从$V$的任何一个顶点开始，长度也是任意的，特别地，可以为0（单个点）。$G$的最小路径覆盖是$G$的所含路径条数$|P|$最少的路径覆盖。
最小路径覆盖数＝$G$的点数$|V|$ - 最小路径覆盖$P$中的边的数目（$P$由边和点组成，且不出现重复点）$\Longrightarrow$ 最小路径覆盖$P$中的边数尽量多，但是又不能让两条边在同一个顶点相交。
- 拆点：将每一个顶点$i$拆成两个顶点$U_i$和$V_i$。
- 根据原图中边的信息，从左半边$U$往右半边$V$引边，所有边的方向都是由$U$到$V$，即如果有边$(u→v)$，则在二分图$G’$中引入边$(U_u→V_v)$。
- 因此，所转化出的二分图$G’$的最大匹配数则是原图$G$中最小路径覆盖上的边数。因此最小路径覆盖数＝原图$G$的顶点数 - 二分图$G’$的最大匹配数便可以得解。
简单证明：最小路径覆盖数＝$G$的点数$|V|$-$G’$的最大匹配数
- 首先，若最大匹配数为0，则二分图$G’$中无边，也就是说图$G$中不存在边，那么显然：最小路径覆盖数=$|V|$ - 最大匹配数=$|V|$ - 0=$|V|$。
- 若此时增加一条匹配边$(U_u→V_v)$，则在图$G$中，u、v在同一条路径上，最小路径覆盖数减少一个。继续增加匹配边，每增加一条，最小路径覆盖数减少一个，则公式：最小路径覆盖数=|V|-$G’$最大匹配数得证。
提取最小路径覆盖？
- 二分图$G’$的最大匹配中的匹配边对应的原图$G$中的边，加上未在边中的顶点，即为最小路径覆盖。

最大匹配与最小点覆盖

顶点覆盖问题：输入一个图$G$和预算$b$，求$b$个能够覆盖到每条边的顶点。
最小覆盖要求用最少的点（假如是二分图，$U$集合或$V$集合的都行），让每条边都至少和其中一个点关联，即假如选了一个点就相当于覆盖了以它为端点的所有边，如何需要选择最少的点来覆盖途图中的所有的边？
König定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数。
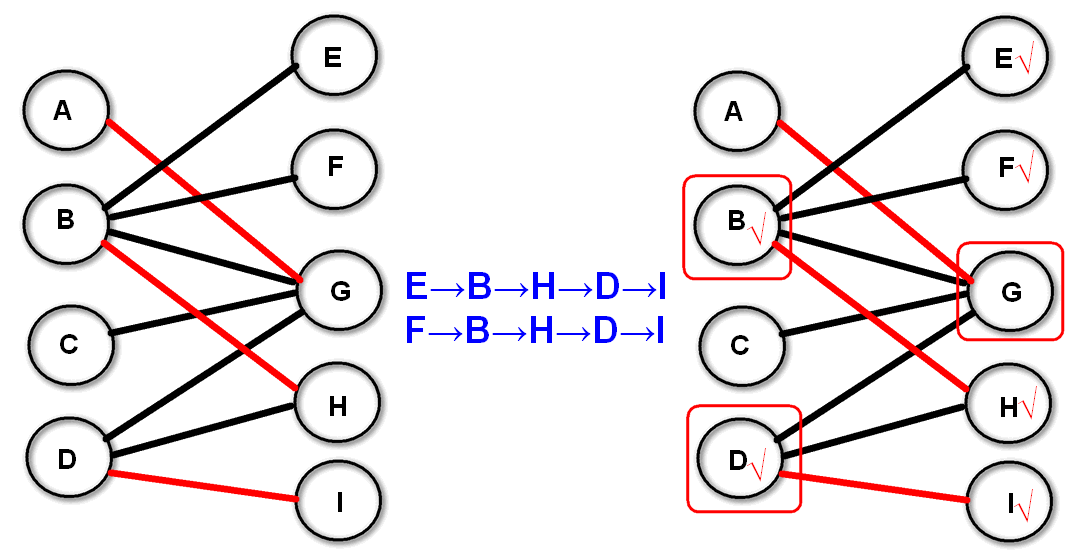
- 如上图，我们已经通过上述的匈牙利算法求出了最大匹配数：$M=3$，最大匹配：$(A→G)、(B→H)、(D→I)$。
- 匈牙利算法需要我们从左半边$U$的某个没有匹配的点，走出一条使得“一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现”的路（交错轨，增广轨）。但是，现在我们已经找到了最大匹配，已经不存在这样的路了。换句话说，我们能寻找到很多可能的增广路，但最后都以找不到“终点是还没有匹配过的点”而失败（如上图$[E→B→H→D→I]$和$[F→B→H→D→I]$）。我们给所有这样的点打上记号（用“√”表示）：从右半边$V$（从左半边$U$出发的增广路径已经在匈牙利算法中搜索过，重复显然没有意义）的所有没有匹配过的点出发，按照增广轨“交替出现”的要求可以走到的所有点（最后走出的路径是很多条不完整的增广路），我们将这些点一一打上标记。
- 那么这些点（红色矩形圈出来的点）组成了最小点覆盖点集：右边所有没有打上记号的点，加上左边已经有记号的点。
König定理简单证明
- 首先，为什么这样得到的点集，点的个数恰好有$M$个呢？
  - 答案很简单，因为这样得到的点集中的每个点都是某条匹配边的其中一个端点。
    - 右边所有没有打上“√”的点和左边已经有“√”的点一定都是匹配边的端点。
      - 如果右半边的哪个点是没有匹配过的，那么它早就当成起点被标记了。
      - 如果左半边的哪个点是没有匹配过的，那就走不到它那里去，否则就找到了一条完整的增广路径，与已经求出最大匹配矛盾。
    - 一条匹配边不可能左端点是标记了的，同时右端点是没标记的，不然的话右边的点就可以经过这条匹配边到达了（右半边到左半边通过非匹配边/左半边到右半边通过匹配边）。
  - 因此，最后我们圈起来的点数与匹配边数。
- 其次，为什么这样得到的点集可以覆盖所有的边呢？
  - 答案同样简单。不可能存在某一条边，它的左端点是没有标记的，而右端点是有标记的。
    - 如果这条边不属于匹配边，那么左端点就可以通过这条边到达（右半边到左半边通过非匹配边/左半边到右半边通过匹配边），从而得到标记。
    - 如果这条边属于我们的匹配边，那么右端点不可能是一条路径的起点，于是它的标记只能是从这条边的左端点过来的（匹配边的右端点不可能作为起点被标记），左端点就应该有标记。
- 最后，为什么这样得到的点集是最小的点覆盖集呢？
  - 这当然是最小的，不可能有比$M$还小的点覆盖集了，因为要覆盖这$M$条匹配边至少就需要$M$个点（匹配边互不相交）。
提取最小点覆盖？
- 通过上述的方法对二分图$G$中的顶点进行标记，$V$中所有没有被打上记号的点，加上$U$中已经有记号的点，即为最小点覆盖。

最大匹配与最大独立数

独立集问题：给定一个图和整数$g$，目标是求图中的$g$个相互独立的顶点，即在任意两个这样的顶点间都不存在相连的边（或者说导出的子图是零图（没有边）的点集）。
简单证明：二分图最大独立集=顶点数-二分图最大匹配
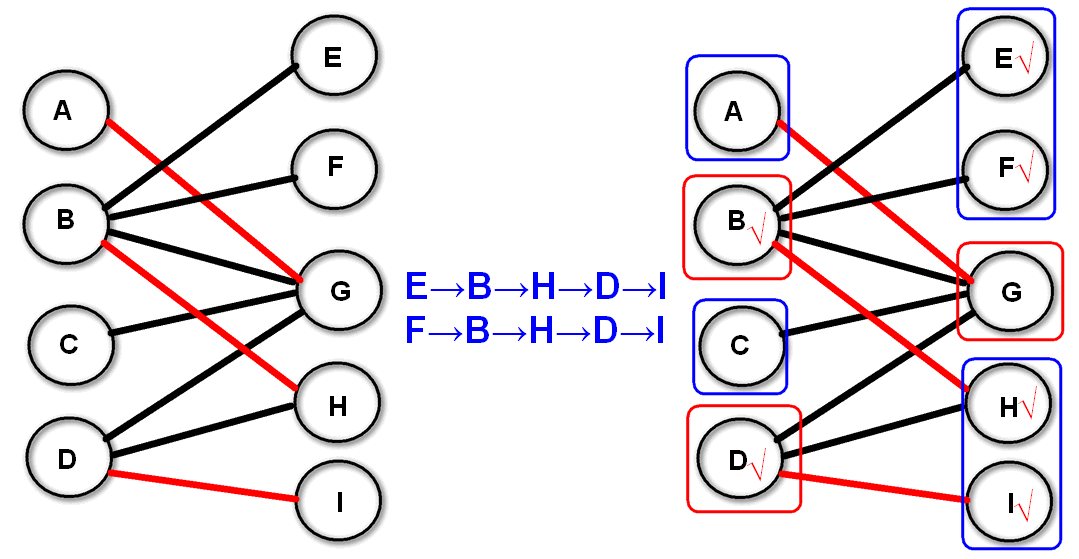
- 上图，我们用红圈圈住的三个点（$B$、$D$、$G$）覆盖了所有边，这是我们证明的前提条件：已经达到最小覆盖，即条件①已经覆盖所有边；条件②所用的点数最小。
- 首先我们来证明其余点（$A$、$C$、$E$、$F$、$H$、$I$）组成的是一个独立集。
  - 如果有两个蓝圈点间有边相连，那么这条边则没有被覆盖，则与条件①矛盾，因此是独立集。
- 再来证明这个独立集是最大的。
  - 如果我们要再增加这个独立集中的点，则需要把某个红圈点变成蓝圈点。而由最小覆盖数=最大匹配数的证明我们知道，每一个红圈点是最大匹配中的一个匹配点，也就是说每个红圈点至少连接了一条边。因此当我们将某个红圈点变成蓝圈点时，我们需要牺牲的蓝圈点的个数是≥1的。也就是说，我们最多只能找到顶点数量相等的其他独立集，而无法找到数量更大的。因此蓝圈点集必定为最大独立集。
  - 蓝圈点数 = 总点数 - 红圈点数，即最大独立集=顶点数 - 最小覆盖集。
- 上面已经证明的König定理：最小点覆盖数=最大匹配数，故有二分图最大独立数=顶点数-二分图最大匹配数。

References

本文标题:算法设计与分析[0016] 二分图匹配问题

文章作者:Gary

发布时间:2017-06-01, 21:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/06/01/Algorithms_BiGraphMatching/