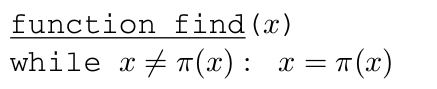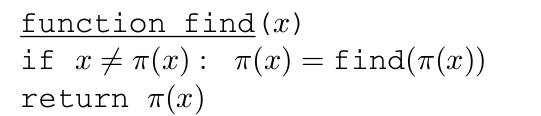2017-06-01

算法设计与分析[0015] Union Find Set（并查集）

并查集

并查集：并查集处理的是集合之间的关系，即 union，find。在这种数据类型中，N个不同元素被分成若干个组，每组是一个集合，这种集合叫做分离集合。并查集支持查找一个元素所属的集合和两个元素分别所属的集合的合并。注意：并查集只能进行合并操作，不能进行分割操作。
并查集支持以下操作：
- makeset(x)：创建一个仅包含 x 的独立集合（分离集）；最初每个节点单独构成了一个分离集 ==> 一组分离集
- find(x)：不断重复地检验节点对，判断其是否属于同一个集合？
- union(x, y)：每当增加了一条边，将与之相关的两个集合合并。
并查集的实现原理
- 并查集是使用树结构实现的
  - 初始化：准备 N 个节点来表示 N 个元素，最开始没有边。
  - 为避免树的退化，对于每棵树，记录其高度 rank。
  - 查询：查询两个节点是否在同一个集合，只需要查询他们是否具有相同的根。
  - 合并：从一个分离集的根向另一个分离集的根连边，这样两棵树就变为了一棵树，也就把两个集合合并为一个了；除非将要合并的树等高，否则将不会出现合并后总高度增加的情形；如果合并时两棵树高度不同，那么从 rank 小的向 rank 大的连边。
  - 路径压缩：每次 find 操作中，当循着一系列的父指针最终找到树的根后，改变所有这些父指针的目标，使其直接指向树根。
    - 通过路径压缩，所有节点的等级都不会发生改变；节点的 rank 不再能解释为其下方子树的高度
    - union 操作只关注树的顶层，路径压缩不会对 union 操作产生影响，它将保持树的顶层不变
    - find 操作（不论是否采用路径压缩）仅仅触及树的内部

并查集实现

#include <iostream>
#include <assert.h>		/* assert */
using namespace std;
 
#define MAX_VERTEX_NUM    26
 
class UnionFindSets {
private:
    int PI[MAX_VERTEX_NUM];
    int rank[MAX_VERTEX_NUM];
    int size;
public:
    UnionFindSets(int size) {
    	this->size = size;
    	for(int vertexIdx=0; vertexIdx<size; vertexIdx++) {
    		PI[vertexIdx] = -1;
    		rank[vertexIdx] = -1;
    	}
    }
    void makeset(int x) {
    	assert(x >= 0 && x < size);
    	PI[x] = x;
    	rank[x] = 0;
    }
    int find(int x) {
    	assert(x >= 0 && x < size);
    	
        // cout << "<find>:" << endl; 
        // cout << "\tPI[" << x << "]: " << PI[x] << endl;
        /*
         * find(PI[x]): backtracking, finding the root node
         * PI[x]=<backtracking result>: 
         *	directly connect the leaf node to the root node to achieve path compression
         */
        if(x != PI[x]) {
        	PI[x] = find(PI[x]);
        }
    	return PI[x];
    }
    void unite(int x, int y) {
    	assert(x >= 0 && x < size);
    	assert(y >= 0 && y < size);
        // cout << "<unite>: " << endl;
        int rx = find(x);
        int ry = find(y);
        // cout << "\t" << x << "["  << rx << "]" << y << "[" << ry << "]" << endl;
    	assert(rx >= 0 && rx < size);
    	assert(ry >= 0 && ry < size);
        if(rx == ry) {
        	return;
        }
        if(rank[rx] > rank[ry]) {
        	PI[ry] = rx;
        }
        else {
            PI[rx] = ry;
            if(rank[rx] == rank[ry]) {
            	rank[ry] += 1;
            }
        }
    }
    void printset() {
    	cout << "<Union&Find set>: " << endl;
    	for(int i=0; i<size; i++) {
    		cout << "\tPI[" << i << "]: " << PI[i]
    			 << "   "
    			 << "rank[" << i << "]: " << rank[i] << endl;
    	}
    }
};

Kruskal 算法

Kruskal 最小生成树算法
- 起始于一个空的图。
- 通过逐条增加边来构造最小生成树：假如在构建最小生成树的过程中，我们已经选择了某些边并在向着正确的方向前进，下一步选择那条边呢？
  - 不断重复地选择未被选中的边中权重最轻的且不会形成环的一条。
    - 为保证连接等价类边的权值最短，算法首先对图中所有边按照权值进行排序。按权值由小到大依次选择边
    - 不会形成环：每次选择一条边加入到现有的部分解中 ===> 需要检验每一条侯选边(u->v) 的端点是否属于不同的连通分量，一旦选定了某条边，则将这条边添加到 MST 并将两个相关的连通分量将被合并。
- Kruskal 最小生成树算法关键数据结构：并查集/分离集 (union-find/disjoint sets)
  - Kruskal 算法开始有 n 个分别包含一个节点的集合（即 n 个分离集）；随着算法的进展，分离集的个数逐渐减少，直到算法的最后一步，分离集的个数变为 1，此时产生最小生成树。
基于并查集的 Kruskal 算法实现：

Kruskal 最小生成树

#include <iostream>
#include <stdio.h>		/* stdin */
#include <limits.h>		/* INT_MAX */
#include <assert.h>		/* assert */
#include <queue>			/* priority_queue */
using namespace std;
  
#define MAX_VERTEX_NUM    26
  
class UnionFindSets {
private:
    int PI[MAX_VERTEX_NUM];
    int rank[MAX_VERTEX_NUM];
    int size;
public:
    UnionFindSets(int size) {
    	this->size = size;
    	for(int vertexIdx=0; vertexIdx<size; vertexIdx++) {
    		PI[vertexIdx] = -1;
    		rank[vertexIdx] = -1;
    	}
    }
    void makeset(int x) {
    	assert(x >= 0 && x < size);
    	PI[x] = x;
    	rank[x] = 0;
    }
    int find(int x) {
    	assert(x >= 0 && x < size);
        // cout << "<find>:" << endl; 
        // cout << "\tPI[" << x << "]: " << PI[x] << endl;
        /*
         * find(PI[x]): backtracking, finding the root node
         * PI[x]=<backtracking result>: 
         *	directly connect the leaf node to the root node to achieve path compression
         */
        if(x != PI[x]) {
        	PI[x] = find(PI[x]);
        }
    	return PI[x];
    }
    void unite(int x, int y) {
    	assert(x >= 0 && x < size);
    	assert(y >= 0 && y < size);
        // cout << "<unite>: " << endl;
        int rx = find(x);
        int ry = find(y);
        // cout << "\t" << x << "["  << rx << "]" << y << "[" << ry << "]" << endl;
    	assert(rx >= 0 && rx < size);
    	assert(ry >= 0 && ry < size);
        if(rx == ry) {
        	return;
        }
        if(rank[rx] > rank[ry]) {
        	PI[ry] = rx;
        }
        else {
            PI[rx] = ry;
            if(rank[rx] == rank[ry]) {
            	rank[ry] += 1;
            }
        }
    }
    void printset() {
    	cout << "<Union&Find set>: " << endl;
    	for(int i=0; i<size; i++) {
    		cout << "\tPI[" << i << "]: " << PI[i]
    			 << "   "
    			 << "rank[" << i << "]: " << rank[i] << endl;
    	}
    }
};
   
struct adjVertexNode {
  int adjVertexIdx;
  int weight;
  adjVertexNode* next;
};
  
struct VertexNode {
  char data;
  int vertexIdx;
  adjVertexNode* list;
  // cost for VertexNode to reach current MST
  int cost;
  // recording the pre-visit VertexNode in the path --> restore a MST
  VertexNode* prev;
};
  
struct Edge {
  int fromIdx, toIdx;
  int weight;
  bool operator< (const Edge& right) const {
    return weight > right.weight;
  };
};
   
struct Graph {
  VertexNode VertexNodes[MAX_VERTEX_NUM];
  int vertexNum;
  int edgeNum;
};
  
void CreateGraph (Graph& g) {
  int i, j, edgeStart, edgeEnd, weight;
  adjVertexNode* adjNode;
  //cout << "Please input vertex and edge num (vertex-num edge-num):" <<endl;
  cin >> g.vertexNum >> g.edgeNum;
  //cout << "Please input vertex information (v1)/n note: every vertex info end with Enter" <<endl;
  for (i=0; i<g.vertexNum; i++) {
    cin >> g.VertexNodes[i].data; // vertex data info.
    g.VertexNodes[i].vertexIdx = i;
    g.VertexNodes[i].list = NULL;
    g.VertexNodes[i].prev = NULL;
  }
  //cout << "input edge information(start end):" << endl;
  for (j=0; j<g.edgeNum; j++)	{
    cin >> edgeStart >> edgeEnd >> weight;
 
    // insert new adjacent VertexNode at the begining of the adjacent list
    adjNode = new adjVertexNode;
    adjNode->adjVertexIdx = edgeEnd;
    adjNode->weight = weight;
    adjNode->next = g.VertexNodes[edgeStart].list;
    g.VertexNodes[edgeStart].list = adjNode;
  }
}
  
void PrintAdjList(const Graph& g) {
  cout << "The adjacent list for graph is:" << endl;
  
  for (int i=0; i < g.vertexNum; i++) {
    cout << " " << g.VertexNodes[i].data << "->";
    adjVertexNode* head = g.VertexNodes[i].list;
    if (head == NULL)
      cout << "NULL";
    while (head != NULL) {
      cout << g.VertexNodes[head->adjVertexIdx].data << "(" << head->weight << ") ";
      head = head->next;
    }
    cout << endl;
  }
}
  
void DeleteGraph(Graph& g) {
  for (int i=0; i<g.vertexNum; i++) {
    adjVertexNode* tmp = NULL;
    while(g.VertexNodes[i].list != NULL) {
      tmp = g.VertexNodes[i].list;
      g.VertexNodes[i].list = g.VertexNodes[i].list->next;
      delete tmp;
      tmp = NULL;
    }
  }
}
  
void Kruskal(Graph& g) {
  UnionFindSets sets(g.vertexNum);
  // use priority_queue for sorting the edges E by weight
  priority_queue<Edge> EdgeQueue;
  for(int i=0; i<g.vertexNum; i++) {
    sets.makeset(g.VertexNodes[i].vertexIdx);
    adjVertexNode* head = g.VertexNodes[i].list;
    while (head != NULL) {
      Edge e;
      e.fromIdx = g.VertexNodes[i].vertexIdx;
      e.toIdx = head->adjVertexIdx;
      e.weight = head->weight;
      EdgeQueue.push(e);

      head = head->next;
    }
  }
  cout << "\nMST constructing: " << endl;
  while(!EdgeQueue.empty()) {
    Edge e = EdgeQueue.top();
    EdgeQueue.pop();
    // cout << "\npop: " << e.fromIdx << "->" << e.toIdx << "(" << e.weight << ")" << endl;
    if(sets.find(e.fromIdx) != sets.find(e.toIdx)) {
      /*
			 * 2 edges with same vertex in an undirect graph
			 *	but every VertexNode can only have on prev.
			 */
      if(g.VertexNodes[e.toIdx].prev != NULL) {
        continue;
      }
      g.VertexNodes[e.toIdx].prev = &g.VertexNodes[e.fromIdx];
      g.VertexNodes[e.toIdx].cost = e.weight;
      cout << "\t+ "
         << g.VertexNodes[e.fromIdx].data << "-->" << g.VertexNodes[e.toIdx].data
         << "(" << e.weight << ")" << endl;
 
      sets.unite(e.fromIdx, e.toIdx);
      // sets.printset();
    }
  }
}
   
// backtracking for the path
void PrintMST(Graph& g) {
  int cost = 0;
  // MST always starts from 0
  for(int i=g.vertexNum-1; i>=0; i--) {
    if(g.VertexNodes[i].prev != NULL) {
      cout << "\t+ "
         << g.VertexNodes[i].data << "<--" << g.VertexNodes[i].prev->data
         << "(" << g.VertexNodes[i].cost << ")" << endl;
       cost += g.VertexNodes[i].cost;
    }
  }
  cout << "   cost: " << cost << endl;
}
  
int main(int argc, const char** argv) {
  freopen("Prim.txt", "r", stdin);
  
  Graph g;
  CreateGraph(g);
  PrintAdjList(g);
  
  Kruskal(g);
   
  cout << endl;
  cout << "Minimum Spanning Tree: " << endl;
  PrintMST(g);
   
  DeleteGraph(g);
  return 0;
}

构建并运行，结果如下：

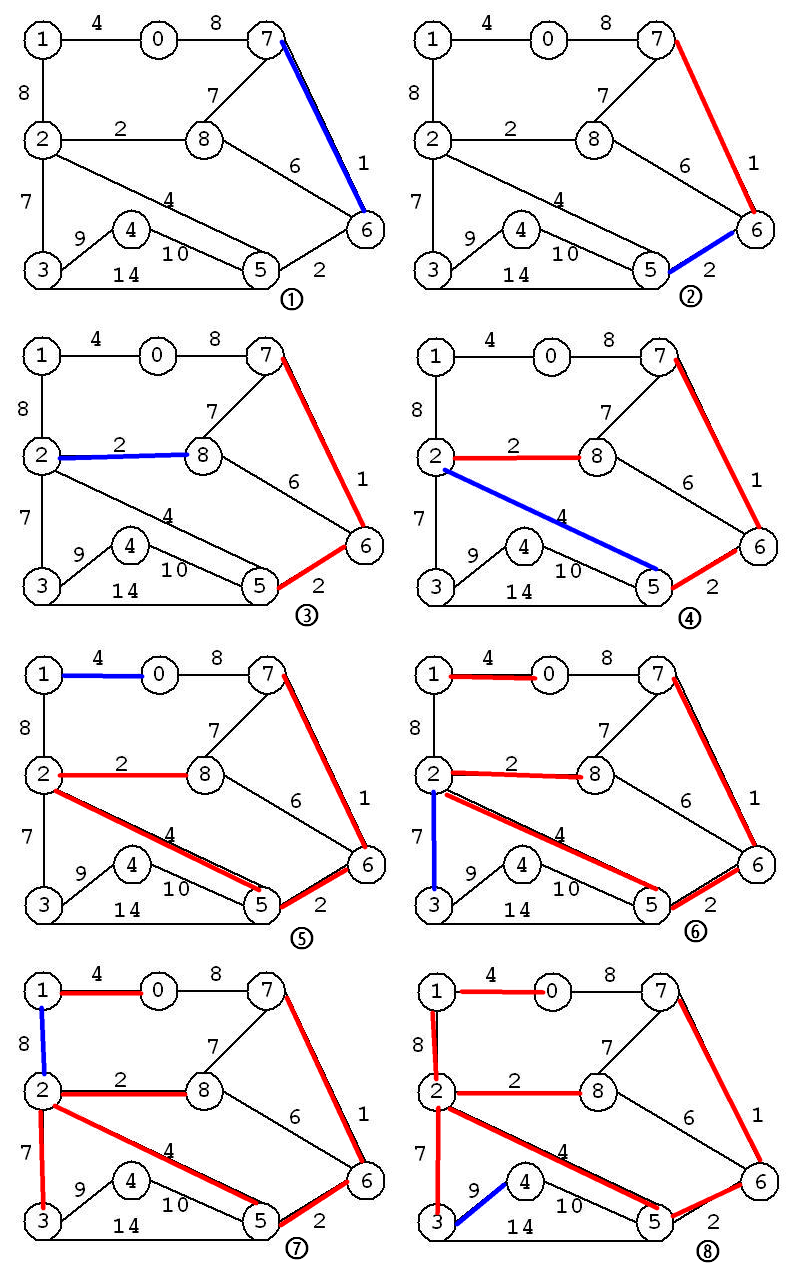
$ g++ Kruskal.cpp -o Kruskal
$ ./Kruskal 
The adjacent list for graph is:
 0->7(8) 1(4) 
 1->2(8) 0(4) 
 2->8(2) 5(4) 3(7) 1(8) 
 3->5(14) 4(9) 2(7) 
 4->5(10) 3(9) 
 5->6(2) 4(10) 3(14) 2(4) 
 6->8(6) 7(1) 5(2) 
 7->8(7) 6(1) 0(8) 
 8->7(7) 6(6) 2(2) 
 
MST constructing: 
  + 6-->7(1)
  + 5-->6(2)
  + 8-->2(2)
  + 2-->5(4)
  + 1-->0(4)
  + 2-->3(7)
  + 2-->1(8)
  + 3-->4(9)
 
Minimum Spanning Tree: 
  + 7<--6(1)
  + 6<--5(2)
  + 5<--2(4)
  + 4<--3(9)
  + 3<--2(7)
  + 2<--8(2)
  + 1<--2(8)
  + 0<--1(4)
   cost: 37

整棵最小生成树的构建过程如下：

Number of Islands

　下面使用并查集解决 岛屿数量 问题，该问题描述如下：

　Given a 2d grid map of ‘1’s (land) and ‘0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:
　11110
　11010
　11000
　00000
Answer: 1

Example 2:
　11000
　11000
　00100
　00011
Answer: 3

问题分析
- 问题实际就是寻找 0-1 2d 网格中由 1 表示的 land 的连通区域块的数目，所以首先是如何确定一个连通区域块，确定之后即可统计整个网格中的块数目即可。
- 可以通过 DFS 确定寻找连通区域块：由上至下/从左及右从一块 land 开始，向右/向下进行 DFS 遍历，当遍历结束时，即到达本岛屿的每一块 land，可以寻找下一块岛屿；为了避免重复遍历，需要将每一块 land 打上标签，标注已属于某个岛屿。
- 一个岛屿即为一个集合，通过遍历每块 land，通过集合的并操作将 land 依次并入各岛屿集合，最终统计岛屿集合的数目即可。

Number of Islands

class UnionFindSets {
private:
    vector<int> PI;
    vector<int> rank;
public:
    UnionFindSets(int size) {
        PI.resize(size);
        rank.resize(size);
        for(int i=0; i<size; i++) {
            PI[i] = -1;
            rank[i] = -1;
        }
    }
    void makeset(int x) {
        PI[x] = x;
        rank[x] = 0;
    }
    int find(int x) {
        if(PI[x] < 0) {
            return -1;
        }
        if(x != PI[x]) {
            PI[x] = find(PI[x]);
        }
        return PI[x];
    }
    void unite(int x, int y) {
        int rx = find(x);
        int ry = find(y);
        if(rx==-1 || ry==-1) {
            return;
        }
        
        if(rx == ry) {
            return;
        }
        if(rank[rx] > rank[ry]) {
            PI[ry] = rx;
        }
        else {
            PI[rx] = ry;
            if(rank[rx] == rank[ry]) {
                rank[ry] += 1;
            }
        }
    }
};
 
class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        if(grid.empty()) {
            return 0;
        }
        
        int rowSize = grid.size();
        int colSize = grid[0].size();
        UnionFindSets sets(rowSize*colSize);
        
        for(int row=0; row<rowSize; row++) {
            for(int col=0; col<colSize; col++) {
                int gridSetIdx = row*colSize + col;
                // water grid not need to make set, still -1
                if(grid[row][col] == '0') {
                    continue;
                }
                else {
                    sets.makeset(gridSetIdx);
                }
                // upper grid is land, need to unite for enlarging land
                if(row>0 && grid[row-1][col]=='1') {
                    int upperSetIdx = (row-1)*colSize + col;
                    sets.unite(gridSetIdx, upperSetIdx);
                }
                // left grid is land, need to unite for enlarging land
                if(col>0 && grid[row][col-1]=='1') {
                    int leftSetIdx = row*colSize + (col-1);
                    sets.unite(gridSetIdx, leftSetIdx);
                }
            }
        }
        // count the number of united sets
        int unitedSetNum = 0;
        unordered_map<int, bool> counted;
        for(int setIdx=0; setIdx<rowSize*colSize; setIdx++) {
            int unitedSetIdx = sets.find(setIdx);
            if(unitedSetIdx == -1) {
                continue;
            }
            if(!counted[unitedSetIdx]) {
                unitedSetNum++;
                counted[unitedSetIdx] = true;
            }
        }
        return unitedSetNum;
    }
};

代码实现细节
- “0” 网格（water）不作为并查集合元素，每一个 “1” 网格（land）一开始为一个集合。
- 如果一个网格为 “1” ，那这个网格和它左方/上方为 “1” 的网格属于一个连通块，并到一个集合。
- 最后，遍历并查集合中的每个元素（忽略了 water 未初始化集合），对其中存在的集合进行计数。

本文标题:算法设计与分析[0015] Union Find Set（并查集）

文章作者:Gary

发布时间:2017-06-01, 14:00:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/06/01/Algorithms_UnionFindSet/