2017-06-26

算法设计与分析[0020] 几个有关图的问题

有向图 vs 无向图

有向图强调出入度的概念；无向图，其邻接矩阵 是一个对称矩阵。
无向图边的两端是对称的，无向图讲究连通这个概念，没有方向，没有拓扑。

判断图是否连通？（一个图有几个连通分量）

从一个指定的点开始，通过不同的策略去遍历这个图，有深度遍历和广度遍历。
每次经过一个节点的时候，首先判断一下这个节点是否已经访问过了，如果没有访问过，则这个节点可以作为下一次继续遍历的候选。
如果这个图是连通的话，这种方法最终会覆盖到整个图。所以可以采用一种计数统计的方式来实现。
- 比如说每次访问一个以前没有遍历的节点，则将对应的计数加一。这样当最后遍历结束后，如果统计的节点和图本身的节点一样的话，表示这个图是连通的，否则表示不连通。
这种方法用来判断整个图是否为连通的时候，实际上只要给定一个点，然后按照给定的步骤可以把该点所连接的所有点都涵盖到。如果有其它分隔的部分则不会再处理了，所以，通过这种办法我们在图不是连通的情况下，它只需要涵盖图的一部分就执行结束了。最坏的情况时间复杂度也就是$O(V+E)$。

连通分量标识符 counter = 1;
visited[] = false;
for 所有节点 ?:
  if(!visited[?])
    dfs(?, visited) 或 bfs(?, visited)
  counter++;
 
counter 为连通分量数目

图中任意两个点的连通性

在某些情况下，我们需要考虑的不仅仅是判断整个图是否为连通这么简单，有时候我们需要考虑，给定两个节点$i, j$，需要判断它们是否相互连接。
- 给定两个点，看它们之间是否连通，可能有很多种情况：比如说当整个图是连通的，则它们必然是连通的；而如果整个图不是连通的，但是这两个点是在一个连通的块，它们也是相互连通的。
- 光遍历一个连通的块是不够的，肯定要遍历完所有的块。另外，如果遍历完一个块仅仅用一个数组来标记是否被访问还是不够的，对于每个不同的连通区域，要进行不同的标识。
  - 遍历图中间所有节点
  - 所有相通的块必须标识为相同：①遍历一遍所有的节点，对每个节点都调用遍历方法，对于已经访问过的节点则直接跳过；②不管是dfs还是bfs，只要给定一个节点遍历完，这一块连通块我们一路做同样的标记就可以了，只要它们相通那么标记也肯定是一样的
实现的细节上
- 考虑用一个计数器和一个数组，对于某个块给计数器设定一个值，然后对应的这个值也放到对应数组的索引的位置里
- 下一次遍历一个新的块时，对这个计数器加一，这样每次遍历的块的计数器值不同。
- 给定任意两个节点，只要判断一下数组里对应的计数器值是否相同就可以判断图中任意两个点是否是连通的。

belongComponent[] = {-1};
counter = 1;
visited[] = false;
for 所有节点?:
  if(!visited[?])
    dfs(?, visited, belongComponent, counter);
  counter++;
 
判断 belongComponent[i] ?= belongComponent[j]
 
void dfs(startIdx, visited, belongComponent, counter) {
  visited[startIdx] = true;
  belongComponent[startIdx] = counter;
  ...
}

深度优先遍历先序&后序

在访问图的时候，假定以深度优先遍历为例。当我们每次遍历到一个节点的时候就访问它，可以称其访问序为前序，而如果等它遍历后递归返回的时候再访问它，这就相当于一个后序。
要实现这两种遍历的方法其实很简单，无非就是在深度优先遍历的时候在访问某个节点前或者在访问结束后将节点加入到队列里。每次在第一次访问某个节点时就往preQueue里面添加元素；而往postQueue里面添加元素，则是在通过该节点以及它所关联的节点都已经遍历结束递归返回的时候。

void void dfs(graph, startIdx) {
  // 先序
  preQueue.push(startIdx);
 
  visited[startIdx] = true;
 
  for 邻接边 startIdx->?:
    if(!visited[?])
      dfs(graph, ?)
 
  // 后序
  postQueue.push(startIdx);
}

图中环的检测

还有一个常见的问题就是检测图中是否存在环？这也是一个很有意思的问题，因为在大多数图的结构中确实是存在环的。
- 对于一个连通的图来说，如果它不存在环，则可以称其为树了（如下文），因此环检测的问题在判断一个图是否为树的问题上有很重要的应用。
从图中构成环的任意一个节点开始，如果按照某个方向遍历，最终它某个可以访问的点是它前面已经遍历过的。
- 对于一些特殊的情况，比如两个相邻的节点之间的连接，它们不能定义为环，需要被排除：可以增加一个参数，表示访问的当前节点的前一个节点，如果从当前节点所能连接到的节点去遍历的时候，碰到的节点是已经访问过的节点，但是这个节点是它的前一个节点的话，这种情况不能定义为环，我们应该忽略。
- 如果对于图并不是完全连通的情况呢？为了避免遗漏，肯定要尝试去遍历所有的节点，和前面检测图连通性类似。

① 遍历所有连通块，记录 prev 节点，同时进行访问标记
② 如果从当前节点所能连接的节点去遍历时，碰到的节点是已经访问过的
  (1) 这个节点是当前节点的 prev 节点，不是环
  (2) 不是 prev 节点，是环
当环存在时，可以通过 prevs[] 数组返回这个环

上述方法仅使用于无向图，对于如下的有向图并不适用：利用上述算法会在节点⑥时检测到环，实际上并不存在环。

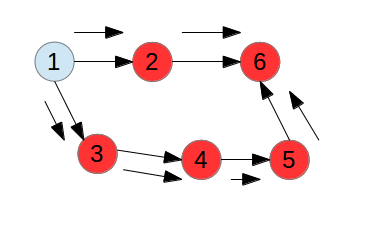
因此对于有向图，需要对上述算法做以下的补充。

③ 找到一个还在遍历中的节点，同时在遍历的时候它如果再次被访问到了，则表示找到了环；如果它被访问完了之后返回，则再次碰到它的时候就不是环了
  (1) bool onStack[]：
    1.1 对这个节点访问前设置，表示在一个递归顺序
    1.2 访问退出这个递归后，设置回来
  (2) bool visited[]：记录访问过的节点
  (3) int prevs[]：记录环的结果，通过记录前后访问的节点来回溯得到环

能够用拓扑排序（下一节）完成对图中所有节点的排序的话，就说明这个图中没有环；如果不能完成，则说明有环。

DAG: 拓扑排序

在一些任务安排和调度的问题里，不同的问题或者任务之间存在一些依赖关系：有的任务需要在某些任务完成之后才能做。像一些学校的教学课程安排：设置某一门课程需要依赖于一个前置的课程，只有学生学习了前置课程之后才能去学习该课程，如果将一门课程当做一个节点，从它引出一个指针指向后序依赖它的课程，就会得到一个有向图。
- 对于这种图来说，最大的特点就是它们肯定就不能存在环，不然就有逻辑上的错误。因此，前面检测一个图是否为DAG的方法就是看图中是否有环。
- 拓扑排序则是在确定没有环的情况下，输出一个正常的序列，这个序列表示从一个不依赖任何元素的节点到后序的节点（这些序列正好符合课程安排或者任务调度的逻辑顺序）。
对于一个有向图来说，如果它不存在环，则它应该为DAG。现在的问题是怎么找出这个拓扑序列来？
- 基于DFS，结合堆栈的拓扑排序
  - 证明：假设对某一已知有向无回路图$G=(V,E)$运行DFS过程，以便确定其顶点的完成时刻。只要证明对任一对不同顶点$u、v∈V$，若$G$中存在一条从$u$到$v$的边，则$finish[v] \lt finish[u]$。考虑过程DFS所探寻的任何边$（u，v）$，当探寻到该边时，顶点$v$必然是已考察完成的顶点或者还未被访问到的顶点：①若$v$是还未被访问到的顶点，则它是$u$的后裔，$finish[v] \lt finish[u]$；②若$v$为已考察完成的顶点，则已完成探索，且$finish[v]$已经设置了。因为仍在探寻$u$，还要为$finish[u]$赋时间戳，同样有$finish[v] \lt finish[u]$。这样一来，对于有向无回路图中任意边$（u, v）$，都有$finish[v]<finish[u]$。
  - 简单解释：如果存在$u$到$v$的通路，则必然存在$finish[u]>finish[v]$，即$u$肯定在$v$的前面（堆栈先进后出）。
- 拓扑序列要求的序列必然是开始于一系列入度为０的节点。如果没有入度为０的节点，则表示这个图不是DAG，这样连遍历都没有必要了（当然，如果这个图里有入度为０的节点，并不代表这个图就一定是DAG）。
  - 怎么来求这些节点的入度：增加一个数组int[] inDegrees，每次我们添加一个边u->v到图里时，inDegrees[v]++。
  - 取这些入度为０的节点，然后从这些节点遍历图。
- 实际上，对于深度优先遍历的后序序列，如果我们将它们的顺序完全倒过来，得到的序列就是拓扑排序序列。
  - 在 DFS 中，依次访问所遍历到的节点；而在拓扑排序时，顶点必须比其邻接点先出现。
  - 用栈来保存拓扑排序的顶点序列，保证在某顶点入栈前，其所有邻接点已入栈。

对所有入度为0的点
  void dfs(int startIdx) {
    visited[startIdx] = true;
    for startIdx->?:
      if(!visited[?])
        dfs(?);
    // 后序深度优先遍历
    topologicalStack.push(startIdx);
  }

上述算法显然不适用与 DAG 不确定的图，假如要检测图中是否存在环，则会最终变成与上一节类似的算法过程。

Kahn 算法
- 计算图中所有点的入度，把入度为0的点加入栈
- 如果栈非空：
  - 取出栈顶顶点a，输出该顶点的值，删除该顶点
  - 从图中删除所有以a为起始点的边，如果删除边后另一个顶点入度为0，则把它入栈
- 如果图中还存在顶点，则表示图中存在环；否则输出的顶点就是一个拓扑排序序列

queue<int> setOfZeroIndegree;
//stack<int> setOfZeroIndegree;
// push 所有入度为0的点
while(!setOfZeroIndegree.empty()) {
  int vertexIdx = setOfZeroIndegree.front();
  //int vertexIdx = setOfZeroIndegree.top();
  setOfZeroIndegree.pop();
 
  // 维护一个拓扑排序序列
  topologicalQueue.push(vertexIdx);
 
  // 遍历由 vertexIdx 引出的所有边 vertexIdx->?
  for ...
    // 通过减少边的数量来模拟将邻边 vertexIdx->? 从图中移除
    edgeNum--;
 
    if(0 == --inDegrees[graph[vertexIdx][?]]) {
      setOfZeroIndegree.push(graph[vertexIdx][?]);
    }
}
 
// 如果此时图中还存在边（点），说明图中含有环路

顶点进栈出栈，其复杂度为$O(V)$；删除顶点后将邻接点的入度减1，其复杂度为$O(E)$；整个算法的复杂度为$O(V+E)$
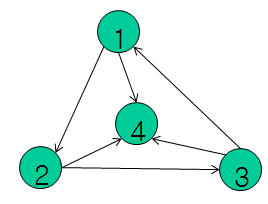
如果利用上面的拓扑排序算法求环，可以判断是否有环，但是输出环时有点麻烦（还是上一节的方法比较直接）$Longrightarrow$ 并不是所有最后剩余的点都是环中的顶点，如下图。

如何判断一个图是否是一棵树？

是连通图
无环

判断一个图是否为二分图？

假设我们有一个图，我们尝试用如下的方式去给每个节点着色，总共所有的节点只能着两种颜色中的一种（假设为红色或者蓝色）。对于一个节点来说，假设它着的是某一种颜色，和它相邻的节点只能着另一种颜色。给定一个图，如果这个图满足上述的特性的话，则这个图可以称之为二分图。
- 判断一个图是否为二分图必然会遍历这个图
- 每次在判断的时候假定一个节点的颜色为某个值，那么再将它相邻的节点颜色都设置成不同的。因为只是两种颜色，可以直接用布尔值类型来处理。
  - 对于不属于二分图的情况，肯定是某个节点访问到一个它可以连接到的节点，而这个节点已经被访问过了，但是这个被访问过的节点和当前节点颜色是一样。这样表明它和前面二分图的定义有冲突，所以，我们遍历整个图就是为了判断是否存在这种情况。
实际实现中需要考虑的细节。
- 对于所有节点对应的颜色需要定义一个boolean[] color数组
- 最开始访问一个节点的时候，将其对应color位设置为true，每次访问一个关联的节点时，将关联节点设置成原来节点的相反值。也就是说，比如节点$v$它的颜色为color[v]，那么下一个它被关联的节点$w$的颜色则可以设置成color[w] = !color[v]，正好通过取反实现了颜色的变换。
- 这里实现的要点还是通过dfs方法
  - 每次碰到一个节点的时候就要判断一下是否已经访问过：①已经访问过的话，要判断颜色是否相同，相同则表明该图不是一个二分图；②没有访问过的话，则将新节点设置成当前节点的相反值。
  - 然后就是要遍历所有节点，防止遗漏未连接的节点情况。

bool[] color;
visited[] = false;
 
for 所有节点 ?:
  if(!visited[?])
    color[?] = true;
    if(!dfs(?, visited, color))
      // 不是二分图
// 为二分图
 
bool dfs(startIdx, visited, color) {
  visited[startIdx] = true;
  for startIdx 邻接边 startIdx->?:
    if(!visited[?]){
      color[?] = !color[startIdx];
      if(!dfs(?, visited, color))
        return false;
    }
    else if(color[startIdx] == color[?]) {
      return false;
    }
  return true;
}

可以看出，一个图是不是二分图并不严格要求其必须是一个连通图。

References

本文标题:算法设计与分析[0020] 几个有关图的问题

文章作者:Gary

发布时间:2017-06-26, 20:26:22

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/06/26/Algorithms_GraphProblems/