2017-07-11

密码学：DES、3DES、AES

　　加密方法可以分为两大类：一类是对称密码体制，又称单钥或私钥密码体制（private key cryptography）；还有一类是非对称密码体制，也称双钥或公开密钥体制（public key cryptography）。前者的加密和解密过程都用同一套密码，后者的加密和解密过程用的是两套密码。
　　在单钥加密的情况下，密钥只有一把，所以密钥的保存变得很重要，一旦秘钥泄露，密文也就被破解了；在双钥加密的情况下，秘钥有两把，一把是公开的公钥，还有一把是不公开的私钥，公钥与私钥是一一对应的关系，有一把公钥就必然有一把与之对应的、独一无二的私钥，反之亦成立。此外，①同时生成公钥和私钥应该是相对比较容易的：所有的公钥、私钥对都不同，用公钥可以解开私钥加密的信息，反之用私钥也可以解开公钥加密的信息；但是②从公钥推算出私钥，应该是很困难或者是不可能的。
　　目前，通用的单钥加密算法有 DES（Data Encryption Standard），通用的双钥加密算法为 RSA（Rivest-Shamir-Adleman），本文主要介绍三种常用的单钥加密算法：DES、3DES（Triple DES）以及 AES（Advanced Encryption Standard）。

DES 算法

DES 算法简介
- DES 算法为密码体制中的对称密码体制，又被称为美国数据加密标准，是 1972 年美国 IBM 公司研制的对称密码体制加密算法；
- DES 是一种用 56 位密钥来加密 64 位数据的方法，密钥长度为 56 位，明文按 64 位进行分组，将分组后的明文组和 56 位的密钥按位替代或交换的方法形成密文组；
- DES 加密算法特点：分组比较短、密钥太短、秘钥生命周期短，运行速度较慢。
DES 工作的基本原理
- 入口参数有三个：key、data、mode
  - key：加密解密使用的密钥
  - data：加密解密的数据
  - mode：工作模式
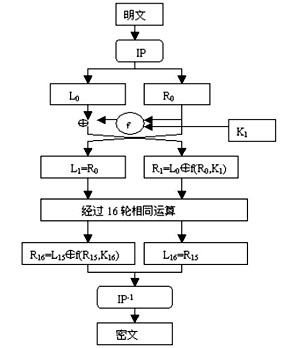
- 当模式为加密模式时，明文按照 64 位进行分组，形成明文组，key 用于对数据加密。
  - 把输入的 64 位数据块经过初始置换按位重新组合，并把输出 $L_0$、$R_0$ 两部分，每部分各长32 位；
  - 然后 $R_0$ 与第一轮子密钥 $K_1$ 进行 $f(R_0, K_1)$ 运算，运算结果再与 $L_0$ 进行按位异或运算，运行结果交换为下一轮的 $R_1$，$R_0$ 交换作为下一轮的 $L_1$；下一轮同样进行 $f(R_i, K_i)$ 运算，以此类推共进行 16 轮；
  - 最后一轮不用进行交换，最后进行逆初始置换，即为密文输出。
- 子密钥 $K_i$（48 bit）生成算法（概述）
  - 初始 key 值为 64 位，但 DES 算法规定，其中第 8、16、…、64 位是奇偶校验位，不参与 DES 运算，故 key 实际可用位数便只有 56 位；
  - 经过缩小选择换位表 1 的变换后，key 的位数由 64 位变成了 56 位，此 56 位分为 $C_0$、$D_0$ 两部分，各 28 位；分别进行第 1 次循环左移，得到 $C_1$、$D_1$，将 $C_1$（28位）、$D_1$（28位）合并得到 56 位，再经过缩小选择换位 2，从而便得到了密钥 $K_0$（48位）；
  - 以此类推，便可得到 $K_1$、$K_2$、…、$K_{15}$，不过需要注意的是，16 次循环左移对应的左移位数要依据下述规则进行：循环左移位数 $1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1$。
- 当模式为解密模式时，key 用于对数据解密
  - DES 的解密过程与加密一样，区别仅仅在于第一次迭代时用子密钥 $K_{15}$、第二次 $K_{14}$、…，最后一次用 $K_0$，算法本身并没有任何变化。
- 在通信网络的两端，双方约定一致的 key，在通信的源点用 key 对核心数据进行 DES 加密，然后以密文形式在公共通信网（如电话网）中传输到通信网络的终点，数据到达目的地后，用同样的 key 对密文数据进行解密，便再现了明码形式的核心数据。
- 实际运用中，密钥只用到了 64 位中的 56 位，这样才具有高的安全性。

密钥的产生：子密钥 $K_i$（48 bit）生成算法

　　DES 含有 16 轮非线性变换，每一轮变换都用一个 48bits 的子密钥，共需 16 个不同的 48bits 的子密钥。一个 64bits 的外部密钥经过以下密钥产生器产生 16 个 48bits 的子密钥。

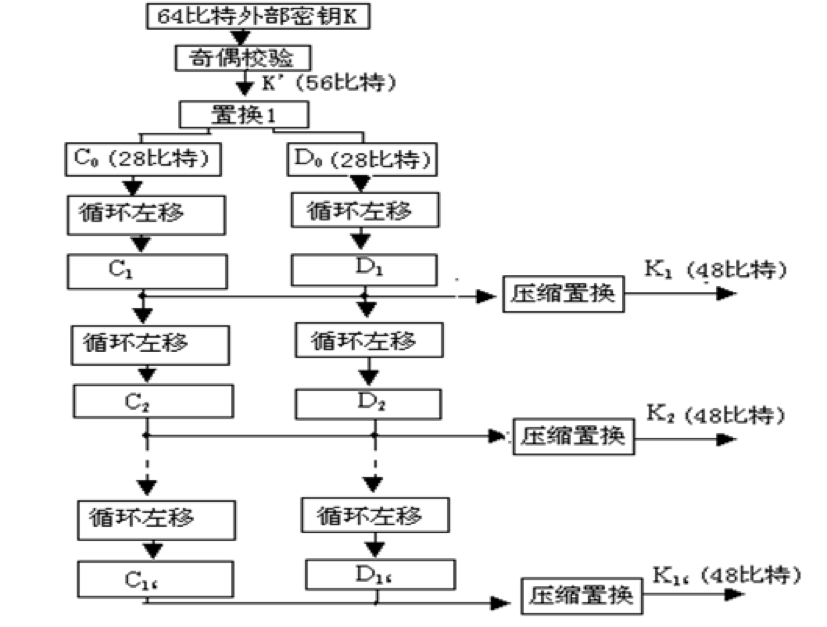
奇偶校验：64 位 $K$ 中第 8、16、…、64 位是奇偶校验位。
置换 1：作用是将 56bits 密钥 $K’$ 各位上的数按规定方式进行换位，置换后的 56bits 分别存到两个 28bits 的寄存器 $C_0$、$D_0$ 中，如下图：
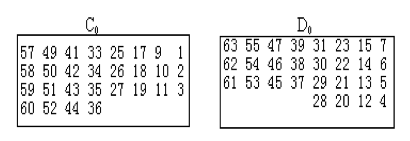
- $C_0$ 的各位依次为原密钥中的第 57、49、41、…、36 位，$D_0$ 的各位依次为原密钥中的第 63、55、47、…、4 位。
循环左移寄存器：每个循环左移寄存器都有 28bits，加密时，循环寄存器 $C_{i+1}$、$D_{i+1}$ 的内容是将循环寄存器 $C_i$、$D_i$ 的内容分别左移 1 至 2 位得到的，各级寄存器移位的比特数如下表：
压缩置换：从 56bits 内容中选出 48bits，产生 16 轮加密的 16 个子密钥，压缩置换表如下：
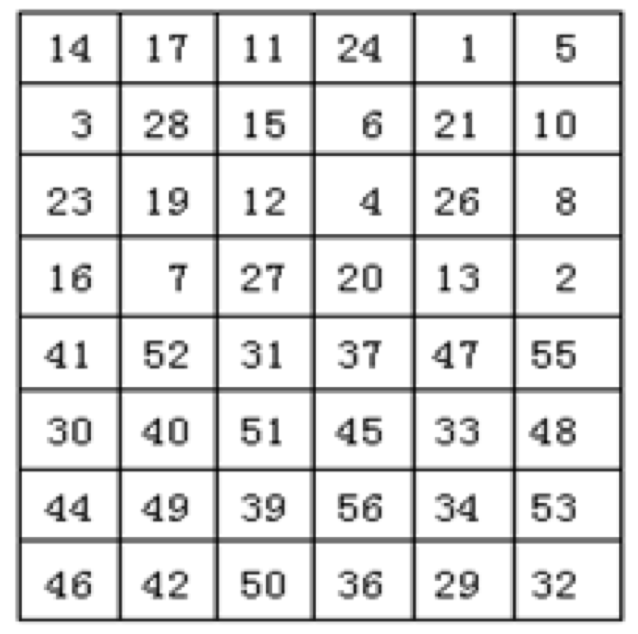
- 压缩置换表中的数字表示循环寄存器对 $(C_i, D_i)$ 的比特序号，读取顺序是从左到右、从上到下，即 $D_i$ 的第 14、17、11、…、32位分别置换成 $C_i$ 的第 1、2、3、…、48位。
具体实现如下void initKey(const char key[8])函数。

// 置换 1 置换表
const int REPLACE_ONE_TABLE[] = {
  57,49,41,33,25,17,9,1,
  58,50,42,34,26,18,10,2,
  59,51,43,35,27,19,11,3,
  60,52,44,36,63,55,47,39,
  31,23,15,7,62,54,46,38,
  30,22,14,6,61,53,45,37,
  29,21,13,5,28,20,12,4
};
// 压缩置换表
const int COMPRESSION_REPLACE_TABLE[] = {
  14,17,11,24,1,5,3,28,
  15,6,21,10,23,19,12,4,
  26,8,16,7,27,20,13,2,
  41,52,31,37,47,55,30,40,
  51,45,33,48,44,49,39,56,
  34,53,46,42,50,36,29,32
};
// 每轮迭代循环左移位数表
const int LEFT_SHIFT_TABLE[] = {
  1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1
};
// 16 轮子密钥
bool subKey[16][48] = {0};
 
//--------------byte转换bit---------------
void bytetobit(bool* out, const char* in, int bitslen){
  for(int i = 0; i < bitslen; i++){
    out[i] = in[i/8]>>(i%8) & 0x1;
  }
}
 
//--------------置换操作---------------
void tableReplace(bool* out, const bool* in, const int* table, int len){
  static bool temp[256];
  for(int i = 0; i < len; i++){
    temp[i] = in[table[i]-1];
  }
  memcpy(out, temp, len);
}
 
//--------------循环左移---------------
void leftLoopShift(bool* in, int len, int loop){
  static bool temp[256];
  memcpy(temp, in, loop);
  memcpy(in, in+loop, len-loop);
  memcpy(in+len-loop, temp, loop);
}
 
/*--------------密钥初始化---------------
 * key[8]: 64 位密钥
 * subKey[16][48]: 16 个 48-bit 子密钥
 */
void initKey(const char key[8]){
  static bool kbit[64],*kl = &kbit[0], *kr = &kbit[28];
  bytetobit(kbit, key, 64);
  // 置换1
  tableReplace(kbit, kbit, REPLACE_ONE_TABLE, 56);
  for(int i = 0; i < 16; i ++){
    leftloop(kl, 28, LEFT_SHIFT_TABLE[i]);
    leftloop(kr, 28, LEFT_SHIFT_TABLE[i]);
    // 压缩置换
    tableReplace(subKey[i], kbit, COMPRESSION_REPLACE_TABLE, 48);
  }
}

明文加密过程

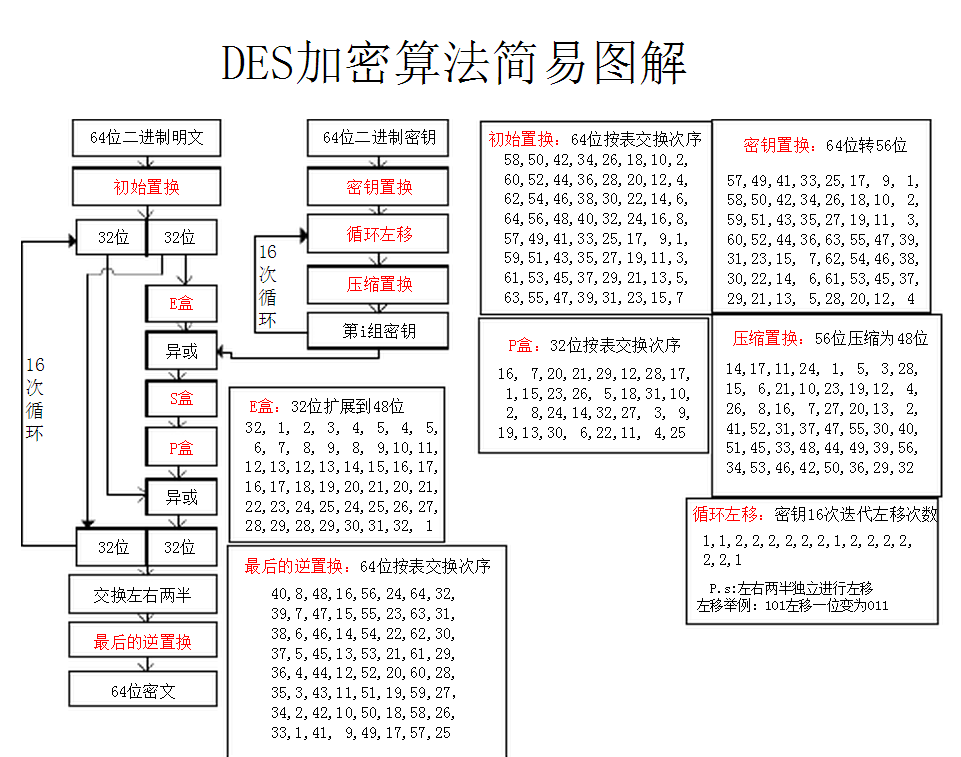
初始置换 $IP$：将 64bits 明文的位置进行置换，得到一个乱序的 64bits 明文组，而后分成左右两段，每段为 32bits，以 $L_0$ 和 $R_0$ 表示；$IP$ 中各列元素位置号相差为 8，相当于将明文各字节按列读出，各列比特经过偶采样和奇采样置换后，再对各行进行逆序。
- 初始置换表 $IP$ 如下：
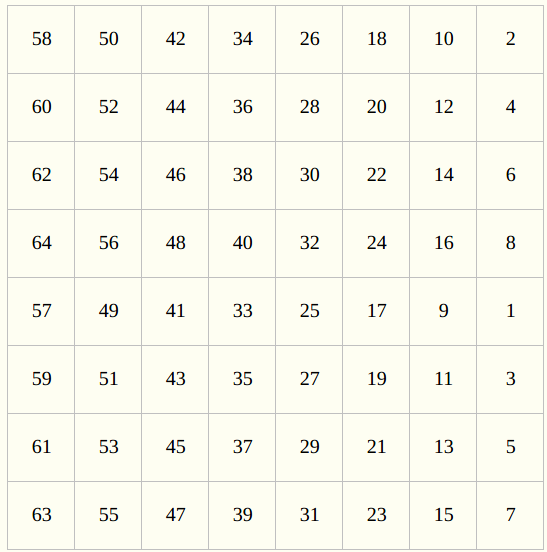
  - 即将初始置换表中的元素按行读出构成置换输出。
  - $IP$ 和最后的 $IP^{-1}$ 在密码上意义不大，它们的作用在于打乱原输入的 ASCII 码字划分的关系，并将原来明文的校验位[8]、[16]、…、[64]变成 $IP$ 输出的一个字节。
乘积变换 $f$：DES 算法的核心部分。
- 将经过 $IP$ 置换后的数据分成 32bits 的左右两组，在迭代过程中彼此左右交换位置。
- 每次迭代时只对右边的 32bits $R_{i-1}$ 进行一系列的加密交换，在此轮迭代即将结束时，把左边的 32bits $L_{i-1}$ 与右边得到的 32bits $R_{i-1}$ 逐位模 2 相加，作为下一轮迭代时右边的段 $R_{i}$，并将原来右边未经变换的段 $R_{i-1}$ 直接送到左边的寄存器作为下一轮迭代时左边的段 $L_i$。
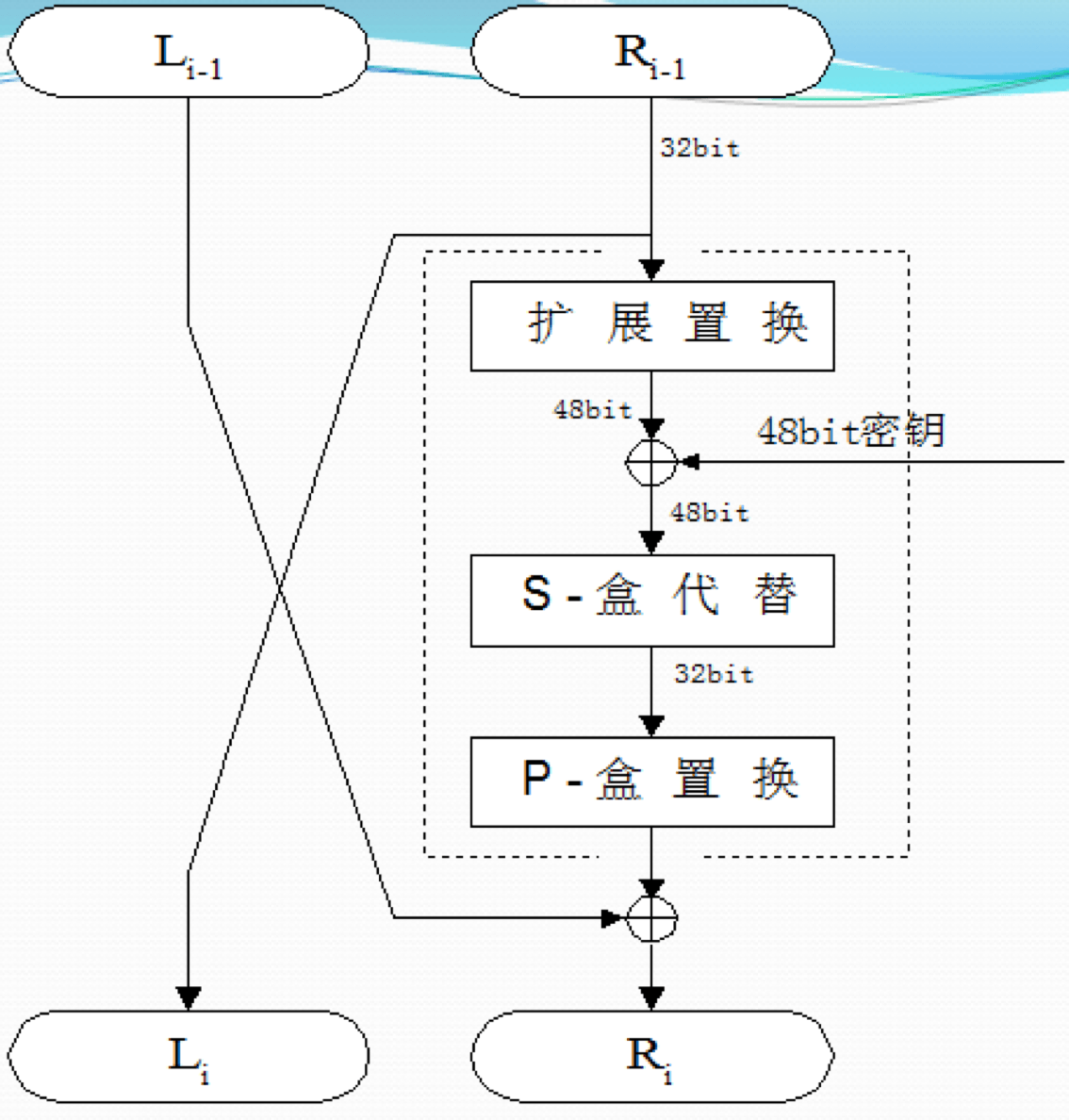
- 在每一轮迭代时，右边的段 $R_{i-1}$ 要经过选择扩展运算 E、密钥加密运算、选择压缩算法 S、置换运算 P 和左右混合运算。
  - 选择扩展运算 E（扩展置换）：将输入的 32bits $R_{i-1}$ 扩展成 48bits 的输出，令 s 表示 E 原输入数据比特的原下标，则 E 的输出是将原下标 $s[ 0或1 (mod 4)]$ 的各比特重复一次得到，即对原来第 1、4、5、8、9、…、32 各位都重复一次，实现数据扩展，将下表中数据按行读出得到 48bits 输出。
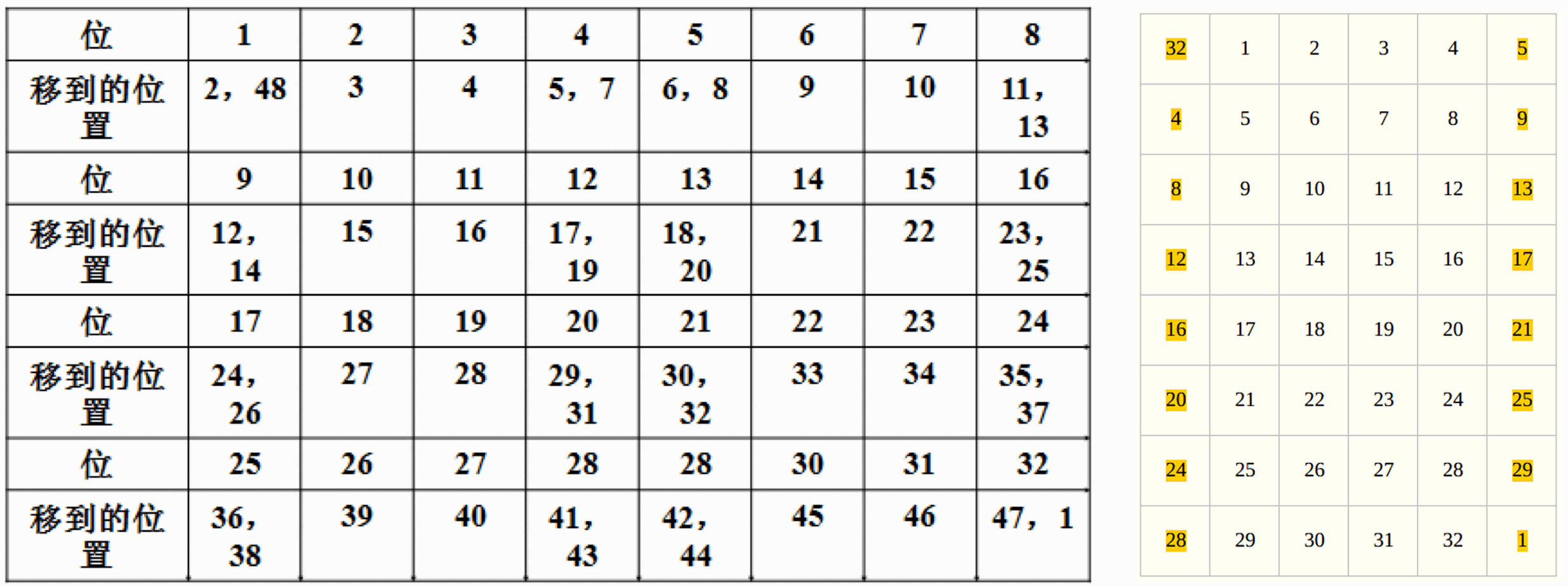
    - 扩展置换的目的有两个：①生成与密钥长度相同的数据以进行异或运算；②提供更长的结果，在后续的替代运算中可以进行压缩。
  - 选择压缩运算 S（S-盒代替）：将前面送来的 48bits 数据自左至右分成 8 组，每组 6bits，而后并行送入 8 个 S-盒，每个 S-盒为一个非线性代换网络，有 4 个输出，如下图：
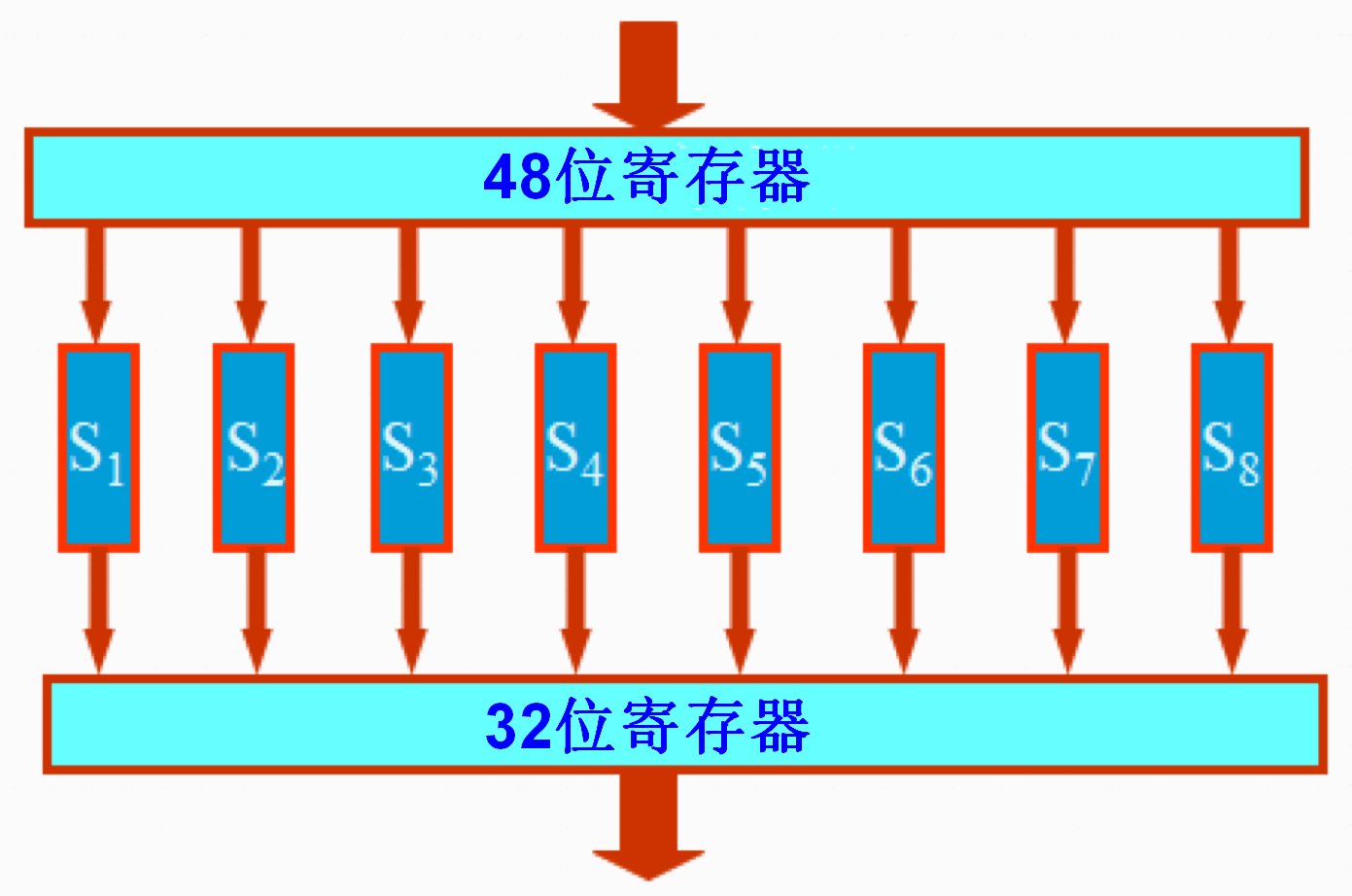
    - 每个 S-盒都是一个 4×16 的矩阵，每行都是 0～15 的数字，但每行的数字排列都不同；每个 S-盒有 6 位输入，4 位输出，6 位输入中的第 1 位和第 6 位数字组成的二进制数值决定置换矩阵的行数，其余 4 位数字所组成的二进制数值决定置换矩阵的列数，行数和列数交点的数字便是 S-盒的输出。
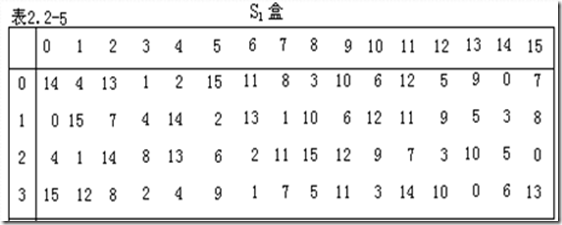
    - 上表是 $S_1$-盒：假设 $S_1$-盒的输入是110010，因第 1 位和第 6 位数字组成的二进制数为：$10_{(2) = 2}$，对应$S_1$-盒行号为 2 的那一行，其余 4 个数字所组成的二进制数为：$1001{(2) = 9}$，对应 $S_1$-盒列号为 9 的那一列，交点处的数是 12，则 $S_1$-盒的输出为1100。
    - S-盒代替是 DES 算法的关键步骤，所有其它的运算都是线性的，易于分析；而 S-盒是非线性的，相比于其它步骤，提供了更好的安全性。
  - 置换运算 P（P-盒置换）：对 $S_1$-至 $S_8$-盒输出的 32bits 数据进行坐标置换，置换表如下：
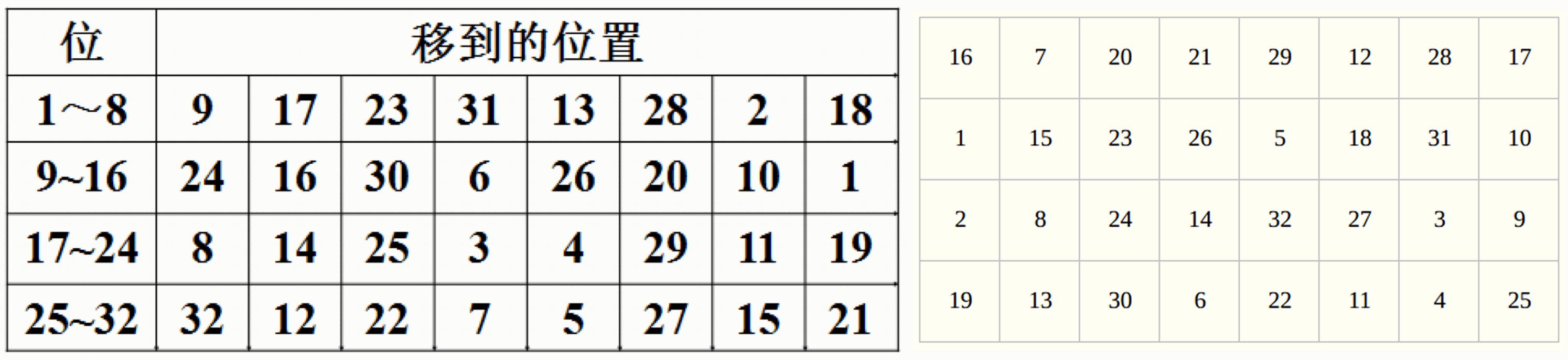
  - 置换 P 输出的 32bits 数据与左边 32bits，即 $R{i-1}$ 逐位模 2 相加（异或运算），所得到的 32bits 作为下一轮迭代用的右边的数字段 $R_i$，并将 $R_{i-1}$ 并行送到左边的寄存器，作为下一轮迭代用的左边的数字段 $L_i$。
逆初始置换 $IP^{-1}$：将 16 轮迭代后给出的 64bits 组进行置换，得到输出的密文组，输出为逆初始置换表中元素按行读得的结果。
- 逆初始置换表 $IP^{-1}$ 如下：
  
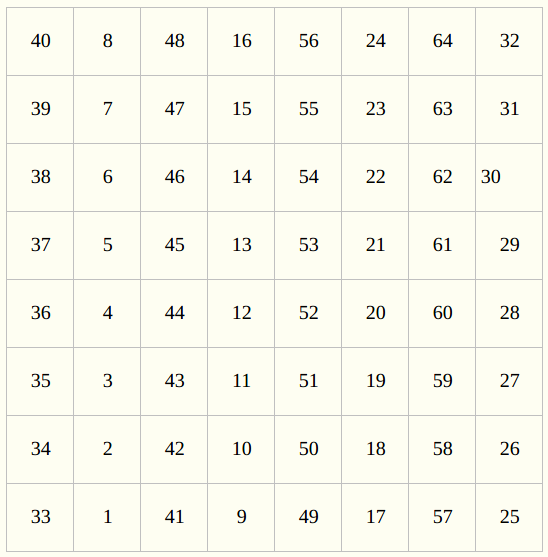
  $\quad$ 逆初始置换是初始置换的逆过程，DES 最后一轮后，左、右两半部分并未进行交换，而是两部分合并形成一个分组作为逆置换的输入，置换方法同上。
具体实现如下void DES(char out[8], char in[8], bool mode=encrypt)函数。

enum {encrypt, decrypt};
// 初始置换表
const int IP_TABLE[] = {
  58,50,42,34,26,18,10,2,
  60,52,44,36,28,20,12,4,
  62,54,46,38,30,22,14,6,
  64,56,48,40,32,24,16,8,
  57,49,41,33,25,17,9,1,
  59,51,43,35,27,19,11,3,
  61,53,45,37,29,21,13,5,
  63,55,47,39,31,23,15,7
};
 
// 逆初始置换表
const int IIP_TABLE[] = {
  40,8,48,16,56,24,64,32,
  39,7,47,15,55,23,63,31,
  38,6,46,14,54,22,62,30,
  37,5,45,13,53,21,61,29,
  36,4,44,12,52,20,60,28,
  35,3,43,11,51,19,59,27,
  34,2,42,10,50,18,58,26,
  33,1,41,9,49,17,57,25
};
// E 位选择表
const int E_TABLE[] = {
  32,1,2,3,4,5,
  4,5,6,7,8,9,
  8,9,10,11,12,13,
  12,13,14,15,16,17,
  16,17,18,19,20,21,
  20,21,22,23,24,25,
  24,25,26,27,28,29,
  28,29,30,31,32,1
};
// S1-S8盒
const char S_BOX[8][4][16] = {
  //S1
  14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
  0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
  4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
  15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13,
  //S2
  15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
  3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
  0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
  13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9,
  //S3
  10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
  13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
  13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
  1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12,
  //S4
  7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
  13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
  10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
  3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14,
  //S5
  2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
  14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
  4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
  11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3,
  //S6
  12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
  10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
  9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
  4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13,
  //S7
  4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
  13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
  1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
  6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12,
  //S8
  13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
  1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
  7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
  2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
};
// P-盒置换表
const int P_TABLE[] = {
  16,7,20,21,29,12,28,17,
  1,15,23,26,5,18,31,10,
  2,8,24,14,32,27,3,9,
  19,13,30,6,22,11,4,25
};
 
//--------------byte转换bit---------------
void bytetobit(bool* out, const char* in, int bitslen){
  for(int i = 0; i < bitslen; i++){
    out[i] = in[i/8]>>(i%8) & 0x1;
  }
}
 
//--------------置换操作---------------
void tableReplace(bool* out, const bool* in, const int* table, int len){
  static bool temp[256];
  for(int i = 0; i < len; i++){
    temp[i] = in[table[i]-1];
  }
  memcpy(out, temp, len);
}
 
//--------------异或操作---------------
void xor(bool* ina, const bool* inb, int len){
  for(int i=0; i<len; i++){
    ina[i] ^= inb[i];
  }
}
 
//--------------S盒变换---------------
void sFunc(bool out[32], const bool in[48]){
  for(int i=0,j,k; i<8; i++,in+=6,out+=4){
    j = (in[0]<<1) + in[5];
    k = (in[1]<<3) + (in[2]<<2) + (in[3]<<1) + in[4];
    bytetobit(out, &S_BOX[i][j][k], 4);
  }
}
 
//--------------密码处理 f 函数---------------
void fFunc(bool in[32], const bool subkey[48]){
  static bool mr[48];
  // E 扩展置换
  tableReplace(mr, in, E_TABLE, 48);
  // 异或操作
  xor(mr, subkey, 48);
  // S-盒代替
  sFunc(in, mr);
  // P-盒置换
    tableReplace(in, in, P_TABLE, 32);
}
 
//--------------bite转换byte---------------
void bittobyte(char* out, const bool* in, int bitslen){
  memset(out, 0, (bitslen+7)/8);
  for(int i=0; i<bitslen; i++){
    out[i/8] |= in[i]<<(i%8);
  }
}
 
//--------------加密解密处理---------------
void DES(char out[8], char in[8], bool mode=encrypt){
  static bool obit[64], temp[32], *li = &obit[0], *ri = &obit[32];
 
  bytetobit(obit, in, 64);
  // 初始置换
  tableReplace(obit, obit, IP_TABLE, 64);
 	// 乘积变换
  if(mode == encrypt) {
    for(int i=0; i<16; i++){
      memcpy(temp, ri, 32);
      fFunc(ri, subKey[i]);
      xor(ri, li, 32);
      memcpy(li, temp, 32);
    }
  }
  else {
    for(int i=15; i>=0; i--){
      memcpy(temp, li, 32);
      fFunc(li, subkey[i]);
      xor(li, ri, 32);
      memcpy(ri, temp, 32);
    }
  }
  // 逆初始置换
  tableReplace(obit, obit, IIP_TABLE, 64);
  bittobyte(out, obit, 64);
}

密文解密过程

DES 是一种 16 轮循环的 Feistel 网络，在 Feistel 网络中，加密的各个步骤称为轮，整个加密过程就是进行若干次轮的循环；无论是任何轮数、任何轮函数，Feistel 网络都可以用相同的结构实现加密和解密，且加密结果必定能够正确解密。
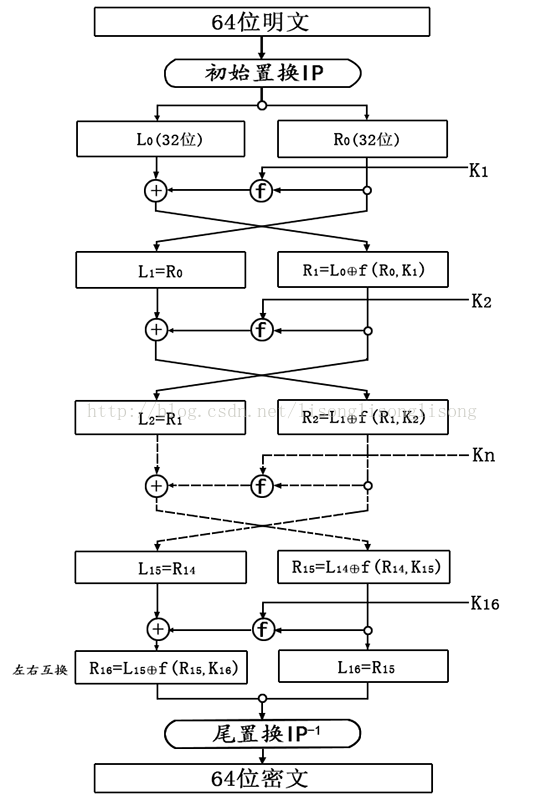
那么，基于 Feistel 网络的 DES 算法如何解密呢？很简单，只要按照逆序来使用子密钥，即输入变成密文，输出则为明文了；此外，需要注意的是，加密过程的最后一轮存在左右互换（如上图），因此在解密过程中，在进入 Feistel 网络之前需要先将经过初始置换的密文左右互换，完成 $L_{16}$、$R_{16}$ 初始化。

// DES 解密
bitset<64> decrypt(bitset<64>& cipher) {
  bitset<64> plain;
  bitset<64> currentBits;
  bitset<32> left;
  bitset<32> right;
  bitset<32> newLeft;
  // 第一步：初始置换IP
  ...
  
  // 第二步：获取 L16 和 R16
  for(int i=32; i<64; ++i)
    left[i-32] = currentBits[i];
  for(int i=0; i<32; ++i)
    right[i] = currentBits[i];
  
  // 第三步：共16轮迭代（子密钥逆序应用）
  for(int round=0; round<16; ++round {
    ... subKey[15-round]
  }
  // 第四步：合并 L0 和 R0，注意合并为 R0L0
  for(int i=0; i<32; ++i)
    plain[i] = left[i];
  for(int i=32; i<64; ++i)
    plain[i] = right[i-32];
  
  // 第五步：逆初始置换
  ...
  
  // 返回明文
  return plain;
}

虽然 56 位密钥的 DES 算法已经风光不在，而且常有用 DES 加密的明文被破译的报道，但目前 DES 算法得到了广泛的应用，在某些场合，仍然发挥着余热。

3DES 算法

3DES 简介
- 密码学中，3DES（Triple DES）是三重数据加密算法（Triple Data Encryption Algorithm）块密码的通称，它相当于是对每个数据块应用三次 DES 加密算法。
- 由于计算机运算能力的增强，原版 DES 密码的密钥长度变得容易被暴力破解；3DES 即是设计用来提供一种相对简单的方法，即通过增加 DES 的密钥长度来避免类似的攻击，而不是设计一种全新的块密码算法。
3DES 加密过程
- 加密算法为：密文 = $E_{K_3}(D_{K_2}(E_{K_1}(明文)))$，其中 $E$ 为 DES 加密操作，$D$ 为 DES 解密操作。
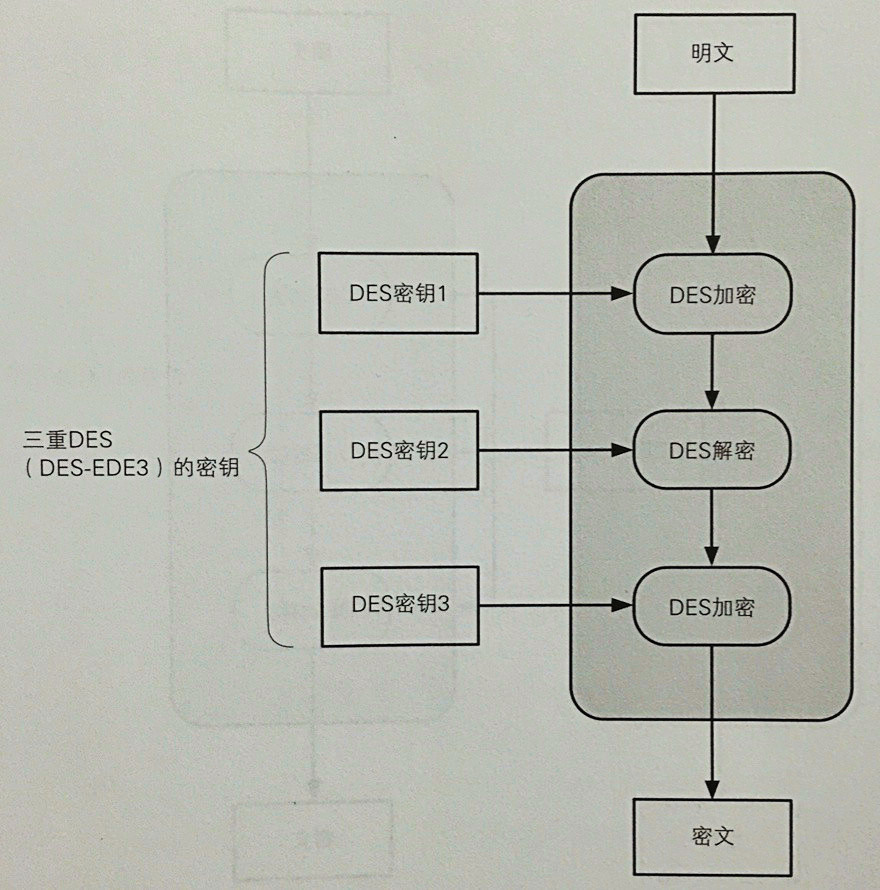
- 3DES 将密钥长度增至 112 位或 168 位，通过增加迭代次数提高安全性；标准定义了三种密钥选项：
  - 密钥选项①：三个密钥独立的，强度最高，拥有 3×56=168 个独立的密钥位；
  - 密钥选项②：$K_1$ 和 $K_2$ 是独立的，而 $K_3 = K_1$，安全性稍低，拥有 2×56=112 个独立的密钥位；
  - 密钥选项③：三个密钥均相等，即 $K_1 = K_2 = K_3$，等同于 DES，只有 56 个密钥位，因为第 1 和第 2 次 DES 操作相互抵消了，因此与 DES 兼容。
3DES 解密过程
- 解密算法为：明文 = $D_{K_3}(E_{K_2}(D_{K_3}(密文)))$，3DES 的解密过程和加密相反，是以密钥 $K_3$、$K_2$、$K_1$ 的顺序进行解密、加密、解密的操作，即将上图从明文到密文的箭头反过来就是解密的流程。
3DES 是 DES 向 AES 过渡的加密算法，3DES 存在以下缺点：处理速度较慢、密钥计算时间较长，加密效率不高。

AES 算法

AES 简介
- 对于三种对称密码，DES 因为已经很容易被暴力破解，因此不建议再使用；3DES 目前还被银行等机构使用，但其处理速度不高，而且在安全性方面也逐渐显现出了一些问题；AES 作为最新标准，安全、快速，而且可以在各种平台上工作，可以算是目前最佳的选择。
- AES 是取代其前任标准 DES 而成为新标准的一种对称密码算法。AES 最终候选算法名单中，总共有 5 种算法，分别为：MARS、RC6、Rijndael、Serpent、Twofish，最终被选定为 AES 的是 Rijndael 算法。
AES 算法（即 Rijndael 算法）是一种对称分组密码算法，数据长度必须是 128bits，使用的密钥长度为 128bits、192bits 或 256bits，对于三种不同长度的 AES 算法，分别称为“AES-128”、“AES-192”、“AES-256”，上图是 AES 加密解密的整体流程图，其中
- 状态（State）：密码运算的中间结果称为状态，状态用以字节为基本构成元素的矩阵阵列来表示，该阵列有 4 行，列数记为 $Nb$，Nb = 分组长度（bits）÷32；
- 密码密钥（Cipher Key）的表示：Cipher Key类似地用一个 4 行的矩阵阵列来表示，列数记为 $Nk$，Nk = 密钥长度（bits）÷32；
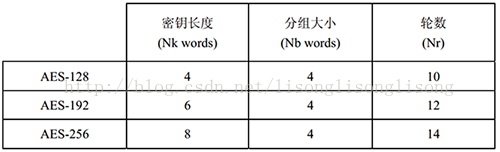
- $Nr$：加密的轮数，对于不同的密钥长度，轮数不一样，具体如上表。
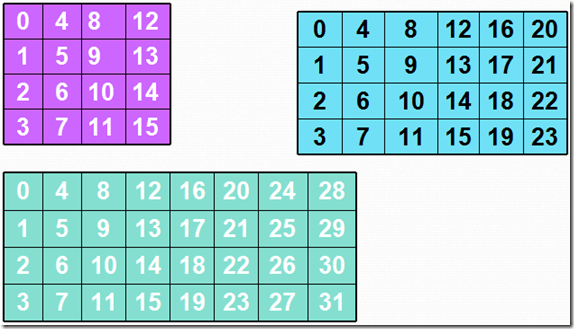
- 算法中 16 字节（128bits）、192bits、256bits 的明文、密文和轮密钥以一个 4×4、4×6、4×8 的矩阵表示，组织排列方式如上，以字节为单位。

密钥扩展

加解密中每轮的密钥分别由初始密钥扩展得到。密钥 bit 的总数 = 分组长度 ×（轮数 + 1）；字总数 = 分组列数 Nb ×（轮数 Nr + 1）。
AES 算法通过密钥扩展（Key Expansion）将用户输入的密钥 K 扩展生成 $Nb(Nr+1)$ 个字，存放在一个线性数组w[Nb*(Nr+1)]中，具体如下：
- 位置变换（RotWord）：接受一个字 [a0, a1, a2, a3] 作为输入，循环左移一个字节后输出 [a1, a2, a3, a0]；
- S-盒变换（SubWord/SubBytes）：S-盒是一个 16×16 的表，其中每一个元素是一个字节；接受一个字 [a0, a1, a2, a3] 的输入，对于输入的每一个字节 ai，前四位 ai[7…4] 组成十六进制数作为行号，后四位 ai[3…0] 组成十六进制数作为列号，查找表中对应的值；最后函数输出 4 个新字节组成的 32-bit 字；
- 轮常数（Rcon）：直接当做常量数组使用；
- 扩展密钥数组w[]的前 $Nk$ 个元素就是外部密钥 $K$，以后的元素w[i]等于它的前一个元素w[i-1]与前 $Nk$ 个元素 w[i-Nk]的异或，即 w[i] = w[i-1] XOR w[i-Nk]；但若 $i$ 为 $Nk$ 的倍数，则 w[i] = w[i-Nk] XOR SubWord(RotWord(w[i-1]) XOR Rcon[i/Nk - 1])$。
- 详细的伪代码如下：

typedef bitset<8> byte;
typedef bitset<32> word;
 
const int Nr = 10;  // AES-128需要 10 轮加密
const int Nk = 4;   // Nk 表示输入密钥的 word 个数
 
// S盒
byte S_BOX[16][16] = {
  /*  0    1    2    3    4    5    6    7    8    9    a    b    c    d    e    f */
  0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, /*0*/ 
  0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, /*1*/
  0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, /*2*/
  0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, /*3*/
  0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, /*4*/
  0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, /*5*/
  0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, /*6*/ 
  0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, /*7*/
  0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, /*8*/
  0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, /*9*/
  0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, /*a*/
  0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, /*b*/
  0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, /*c*/
  0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, /*d*/
  0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, /*e*/
  0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16  /*f*/
};
  
// 将4个 byte 转换为一个 word.
word Word(byte& k1, byte& k2, byte& k3, byte& k4) {
  word result(0x00000000);
  word temp;
  temp = k1.to_ulong();  // K1
  temp <<= 24;
  result |= temp;
  temp = k2.to_ulong();  // K2
  temp <<= 16;
  result |= temp;
  temp = k3.to_ulong();  // K3
  temp <<= 8;
  result |= temp;
  temp = k4.to_ulong();  // K4
  result |= temp;
  return result;
}
  
/**
 *  按字节 循环左移一位
 *  即把[a0, a1, a2, a3]变成[a1, a2, a3, a0]
 */
word RotWord(word& rw) {
  word high = rw << 8;
  word low = rw >> 24;
  return high | low;
}
 
/**
 *  对输入word中的每一个字节进行S-盒变换
 */
word SubWord(word& sw) {
  word temp;
  for(int i=0; i<32; i+=8) {
    int row = sw[i+7]*8 + sw[i+6]*4 + sw[i+5]*2 + sw[i+4];
    int col = sw[i+3]*8 + sw[i+2]*4 + sw[i+1]*2 + sw[i];
    byte val = S_Box[row][col];
    for(int j=0; j<8; ++j)
      temp[i+j] = val[j];
  }
  return temp;
}
 
/**
 *  密钥扩展函数 - 对Nk-word密钥进行扩展得到 w[4*(Nr+1)]
 */ 
void KeyExpansion(byte key[4*Nk], word w[4*(Nr+1)])
{
  word temp;
  int i = 0;
  // w[]的前4个就是输入的key
  while(i < Nk) {
    w[i] = Word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]);
    ++i;
  }
 
  i = Nk;
 
  while(i < 4*(Nr+1)){
    temp = w[i-1]; // 记录前一个word
    if(i % Nk == 0)
      w[i] = w[i-Nk] ^ SubWord(RotWord(temp)) ^ Rcon[i/Nk-1];
    else 
      w[i] = w[i-Nk] ^ temp;
    ++i;
  }
}

从扩展密钥中取出轮密钥：第一个轮密钥由扩展密钥的第一个 $Nb$ 个字（4 字节），第二个轮密钥由接下来的 $Nb$ 个字组成，一次类推。
加密过程
依据本节开头的 AES 流程图可以得到下图的伪代码：
- 从伪代码描述中可以看出，AES 加密时主要涉及以下几个步骤
  - 字节替换（SubBytes）就是根据一张替换表（S-Box），将输入中每个字节的值替换成另一个字节的值，在密钥扩展部分已经介绍了；
  - 行移位（ShiftRows）即将 SubBytes 的输出以字节为单位进行打乱出路，这种打乱处理也是有规律的：通过作用于行上的循环左移，第 0 行不变，第 1 行循环移位 $C1$ 字节，第 2 行循环移位 $C2$ 字节，第 3 行循环移位 $C3$ 字节，如下图：
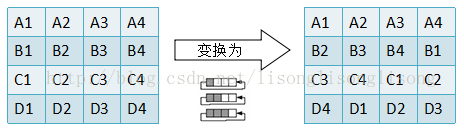
    $\quad$ 偏移量 $C1$、$C2$、$C3$ 与分组长度 $Nb$ 有关，如下表所示：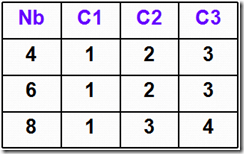
  - 列混淆（MixColumns）即对一个 4 字节的值进行变换，将其变成另外一个 4 字节的值，变换方式如下：
    
    $\quad$ 注意公式中用到的乘法是伽罗华域（$GF(2^8)$，有限域）上的乘法。
  - 轮密钥加（AddRoundKey）：扩展密钥只参与了这一步，就是将 MixColumns 的输出与轮密钥进行按位 XOR 处理，至此，一轮就结束了。

typedef bitset<8> byte;
typedef bitset<32> word;
 
const int Nr = 10;  // AES-128需要 10 轮加密
const int Nk = 4;   // Nk 表示输入密钥的 word 个数
 
// S盒
byte S_BOX[16][16] = {
  /*  0    1    2    3    4    5    6    7    8    9    a    b    c    d    e    f */
  0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76, /*0*/ 
  0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0, /*1*/
  0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15, /*2*/
  0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75, /*3*/
  0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84, /*4*/
  0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf, /*5*/
  0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8, /*6*/ 
  0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2, /*7*/
  0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73, /*8*/
  0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb, /*9*/
  0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79, /*a*/
  0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08, /*b*/
  0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a, /*c*/
  0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e, /*d*/
  0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf, /*e*/
  0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16  /*f*/
};
 
// S盒变换 -每个字节前4位为行号，后4位为列号
void SubBytes(byte mtx[4*4]) {
  for(int i=0; i<16; ++i) {
    int row = mtx[i][7]*8 + mtx[i][6]*4 + mtx[i][5]*2 + mtx[i][4];
    int col = mtx[i][3]*8 + mtx[i][2]*4 + mtx[i][1]*2 + mtx[i][0];
    mtx[i] = S_Box[row][col];
  }
}
 
// 行变换 - 按字节循环移位
void ShiftRows(byte mtx[4*4]) {
  // 第二行循环左移一位
  byte temp = mtx[4];
  for(int i=0; i<3; ++i)
    mtx[i+4] = mtx[i+5];
  mtx[7] = temp;
  // 第三行循环左移两位
  for(int i=0; i<2; ++i) {
    temp = mtx[i+8];
    mtx[i+8] = mtx[i+10];
    mtx[i+10] = temp;
  }
  // 第四行循环左移三位
  temp = mtx[15];
  for(int i=3; i>0; --i)
    mtx[i+12] = mtx[i+11];
  mtx[12] = temp;
}
 
// 有限域上的乘法 GF(2^8)
byte GFMul(byte a, byte b) { 
  byte p = 0;
  byte hi_bit_set;
  for (int counter = 0; counter < 8; counter++) {
    if ((b & byte(1)) != 0) {
      p ^= a;
    }
    hi_bit_set = (byte) (a & byte(0x80));
    a <<= 1;
    if (hi_bit_set != 0) {
      a ^= 0x1b; /* x^8 + x^4 + x^3 + x + 1 */
    }
    b >>= 1;
  }
  return p;
}
 
// 列混淆
void MixColumns(byte mtx[4*4]) {
  byte arr[4];
  for(int i=0; i<4; ++i) {
    for(int j=0; j<4; ++j)
      arr[j] = mtx[i+j*4];
 
    mtx[i] = GFMul(0x02, arr[0]) ^ GFMul(0x03, arr[1]) ^ arr[2] ^ arr[3];
    mtx[i+4] = arr[0] ^ GFMul(0x02, arr[1]) ^ GFMul(0x03, arr[2]) ^ arr[3];
    mtx[i+8] = arr[0] ^ arr[1] ^ GFMul(0x02, arr[2]) ^ GFMul(0x03, arr[3]);
    mtx[i+12] = GFMul(0x03, arr[0]) ^ arr[1] ^ arr[2] ^ GFMul(0x02, arr[3]);
  }
}
 
// 轮密钥加变换 - 将每一列与扩展密钥进行异或
void AddRoundKey(byte mtx[4*4], word k[4]) {
  for(int i=0; i<4; ++i) {
    word k1 = k[i] >> 24;
    word k2 = (k[i] << 8) >> 24;
    word k3 = (k[i] << 16) >> 24;
    word k4 = (k[i] << 24) >> 24;
    
    mtx[i] = mtx[i] ^ byte(k1.to_ulong());
    mtx[i+4] = mtx[i+4] ^ byte(k2.to_ulong());
    mtx[i+8] = mtx[i+8] ^ byte(k3.to_ulong());
    mtx[i+12] = mtx[i+12] ^ byte(k4.to_ulong());
  }
}
 
// 加密
void encrypt(byte in[4*4], word w[4*(Nr+1)]) {
  word key[4];
  for(int i=0; i<4; ++i)
    key[i] = w[i];
  AddRoundKey(in, key);
 
  for(int round=1; round<Nr; ++round){
    SubBytes(in);
    ShiftRows(in);
    MixColumns(in);
    for(int i=0; i<4; ++i)
      key[i] = w[4*round+i];
    AddRoundKey(in, key);
  }
 
  SubBytes(in);
  ShiftRows(in);
  for(int i=0; i<4; ++i)
    key[i] = w[4*Nr+i];
  AddRoundKey(in, key);
}

解密过程

①AES 使用的并不是 Feistel 网络，而是 SPN 结构，加密时的 SubBytes、ShiftRows、MixColumns，解密时分别为反向运算的 InvSubBytes、InvShiftRows、InvMixColumns，这是因为 SPN 结构不像 Feistel 网络一样能够用一种结构实现加密和解密；②加解密所有操作的顺序正好是相反的；正是这两点，保证了解密能够正确地恢复明文。
依据本节开头的 AES 流程图可以得到下图的伪代码：
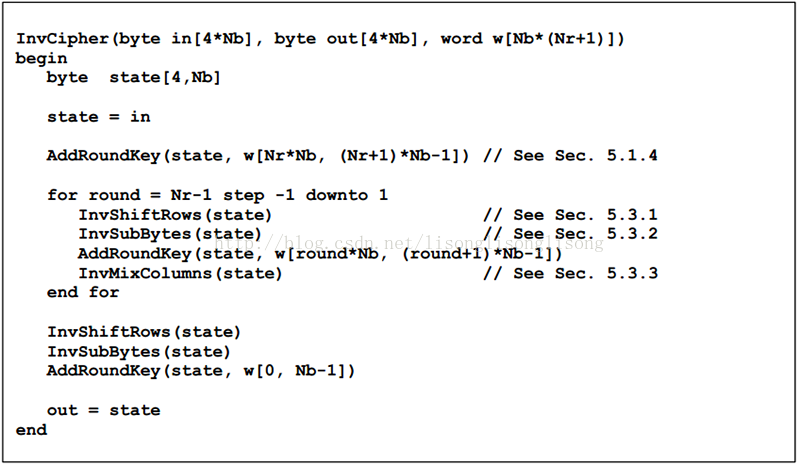
- 从伪代码描述中可以看出，AES 解密时主要涉及以下几个步骤
  - 逆行移位（InvShiftRows）：加密时是对矩阵每一行进行循环左移，所以解密时的 InvShiftRows 操作是对矩阵每一行进行循环右移；
  - 逆字节替换（InvSubBytes）：与加密时的字节替换一样也是查表，查表的方式也一样，只不过查的是另外一张表，S-Box 的逆表；
  - 逆列混淆（MixColumns）：与加密时的列混淆一样，只不过变换公式中的系数矩阵发生了变化，如下图：
  - 轮密钥加（AddRoundKey）：与加密时的操作一致。

typedef bitset<8> byte;
typedef bitset<32> word;
 
const int Nr = 10;  // AES-128需要 10 轮加密
const int Nk = 4;   // Nk 表示输入密钥的 word 个数
 
// S-盒逆表
byte INV_S_BOX[16][16] = {
  /*  0    1    2    3    4    5    6    7    8    9    a    b    c    d    e    f  */ 
  0x52,0x09,0x6a,0xd5,0x30,0x36,0xa5,0x38,0xbf,0x40,0xa3,0x9e,0x81,0xf3,0xd7,0xfb, /*0*/
  0x7c,0xe3,0x39,0x82,0x9b,0x2f,0xff,0x87,0x34,0x8e,0x43,0x44,0xc4,0xde,0xe9,0xcb, /*1*/
  0x54,0x7b,0x94,0x32,0xa6,0xc2,0x23,0x3d,0xee,0x4c,0x95,0x0b,0x42,0xfa,0xc3,0x4e, /*2*/
  0x08,0x2e,0xa1,0x66,0x28,0xd9,0x24,0xb2,0x76,0x5b,0xa2,0x49,0x6d,0x8b,0xd1,0x25, /*3*/
  0x72,0xf8,0xf6,0x64,0x86,0x68,0x98,0x16,0xd4,0xa4,0x5c,0xcc,0x5d,0x65,0xb6,0x92, /*4*/
  0x6c,0x70,0x48,0x50,0xfd,0xed,0xb9,0xda,0x5e,0x15,0x46,0x57,0xa7,0x8d,0x9d,0x84, /*5*/
  0x90,0xd8,0xab,0x00,0x8c,0xbc,0xd3,0x0a,0xf7,0xe4,0x58,0x05,0xb8,0xb3,0x45,0x06, /*6*/
  0xd0,0x2c,0x1e,0x8f,0xca,0x3f,0x0f,0x02,0xc1,0xaf,0xbd,0x03,0x01,0x13,0x8a,0x6b, /*7*/
  0x3a,0x91,0x11,0x41,0x4f,0x67,0xdc,0xea,0x97,0xf2,0xcf,0xce,0xf0,0xb4,0xe6,0x73, /*8*/
  0x96,0xac,0x74,0x22,0xe7,0xad,0x35,0x85,0xe2,0xf9,0x37,0xe8,0x1c,0x75,0xdf,0x6e, /*9*/
  0x47,0xf1,0x1a,0x71,0x1d,0x29,0xc5,0x89,0x6f,0xb7,0x62,0x0e,0xaa,0x18,0xbe,0x1b, /*a*/
  0xfc,0x56,0x3e,0x4b,0xc6,0xd2,0x79,0x20,0x9a,0xdb,0xc0,0xfe,0x78,0xcd,0x5a,0xf4, /*b*/
  0x1f,0xdd,0xa8,0x33,0x88,0x07,0xc7,0x31,0xb1,0x12,0x10,0x59,0x27,0x80,0xec,0x5f, /*c*/
  0x60,0x51,0x7f,0xa9,0x19,0xb5,0x4a,0x0d,0x2d,0xe5,0x7a,0x9f,0x93,0xc9,0x9c,0xef, /*d*/
  0xa0,0xe0,0x3b,0x4d,0xae,0x2a,0xf5,0xb0,0xc8,0xeb,0xbb,0x3c,0x83,0x53,0x99,0x61, /*e*/
  0x17,0x2b,0x04,0x7e,0xba,0x77,0xd6,0x26,0xe1,0x69,0x14,0x63,0x55,0x21,0x0c,0x7d  /*f*/
};
 
// 逆行变换 - 以字节为单位循环右移
void InvShiftRows(byte mtx[4*4]) {
  // 第二行循环右移一位
  byte temp = mtx[7];
  for(int i=3; i>0; --i)
    mtx[i+4] = mtx[i+3];
  mtx[4] = temp;
  // 第三行循环右移两位
  for(int i=0; i<2; ++i) {
    temp = mtx[i+8];
    mtx[i+8] = mtx[i+10];
    mtx[i+10] = temp;
  }
  // 第四行循环右移三位
  temp = mtx[12];
  for(int i=0; i<3; ++i)
    mtx[i+12] = mtx[i+13];
  mtx[15] = temp;
}
 
// 逆字节替换
void InvSubBytes(byte mtx[4*4]) {
  for(int i=0; i<16; ++i) {
    int row = mtx[i][7]*8 + mtx[i][6]*4 + mtx[i][5]*2 + mtx[i][4];
    int col = mtx[i][3]*8 + mtx[i][2]*4 + mtx[i][1]*2 + mtx[i][0];
    mtx[i] = Inv_S_Box[row][col];
  }
}
 
// 有限域上的乘法 GF(2^8)
byte GFMul(byte a, byte b) { 
  byte p = 0;
  byte hi_bit_set;
  for (int counter = 0; counter < 8; counter++) {
    if ((b & byte(1)) != 0) {
      p ^= a;
    }
    hi_bit_set = (byte) (a & byte(0x80));
    a <<= 1;
    if (hi_bit_set != 0) {
      a ^= 0x1b; /* x^8 + x^4 + x^3 + x + 1 */
    }
    b >>= 1;
  }
  return p;
}
 
// 逆列混淆
void InvMixColumns(byte mtx[4*4]) {
  byte arr[4];
  for(int i=0; i<4; ++i) {
    for(int j=0; j<4; ++j)
      arr[j] = mtx[i+j*4];
 
    mtx[i] = GFMul(0x0e, arr[0]) ^ GFMul(0x0b, arr[1]) 
      ^ GFMul(0x0d, arr[2]) ^ GFMul(0x09, arr[3]);
    mtx[i+4] = GFMul(0x09, arr[0]) ^ GFMul(0x0e, arr[1]) 
      ^ GFMul(0x0b, arr[2]) ^ GFMul(0x0d, arr[3]);
    mtx[i+8] = GFMul(0x0d, arr[0]) ^ GFMul(0x09, arr[1]) 
      ^ GFMul(0x0e, arr[2]) ^ GFMul(0x0b, arr[3]);
    mtx[i+12] = GFMul(0x0b, arr[0]) ^ GFMul(0x0d, arr[1]) 
      ^ GFMul(0x09, arr[2]) ^ GFMul(0x0e, arr[3]);
  }
}
 
// 轮密钥加变换 - 将每一列与扩展密钥进行异或
void AddRoundKey(byte mtx[4*4], word k[4]) {
  for(int i=0; i<4; ++i) {
    word k1 = k[i] >> 24;
    word k2 = (k[i] << 8) >> 24;
    word k3 = (k[i] << 16) >> 24;
    word k4 = (k[i] << 24) >> 24;
     
    mtx[i] = mtx[i] ^ byte(k1.to_ulong());
    mtx[i+4] = mtx[i+4] ^ byte(k2.to_ulong());
    mtx[i+8] = mtx[i+8] ^ byte(k3.to_ulong());
    mtx[i+12] = mtx[i+12] ^ byte(k4.to_ulong());
  }
}
 
// 解密
void decrypt(byte in[4*4], word w[4*(Nr+1)]) {
  word key[4];
  for(int i=0; i<4; ++i)
    key[i] = w[4*Nr+i];
  AddRoundKey(in, key);
 
  for(int round=Nr-1; round>0; --round) {
    InvShiftRows(in);
    InvSubBytes(in);
    for(int i=0; i<4; ++i)
      key[i] = w[4*round+i];
    AddRoundKey(in, key);
    InvMixColumns(in);
  }
 
  InvShiftRows(in);
  InvSubBytes(in);
  for(int i=0; i<4; ++i)
    key[i] = w[i];
  AddRoundKey(in, key);
}

References

本文标题:密码学：DES、3DES、AES

文章作者:Gary

发布时间:2017-07-11, 18:02:16

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/07/11/programPearls_DES$3DES$AES/