2017-07-11

JPEG编码&算术编码、LZW编码

　　本文介绍 JPEG 编解码过程（附简单的cpp实现）。JPEG 中常用到的熵编码是变长编码：Huffman 编码，本文也对算术编码（附cpp实现）、LZW 编码（附py实现）两种熵编码进行介绍。

JPEG 编解码过程

JPEG 编码过程
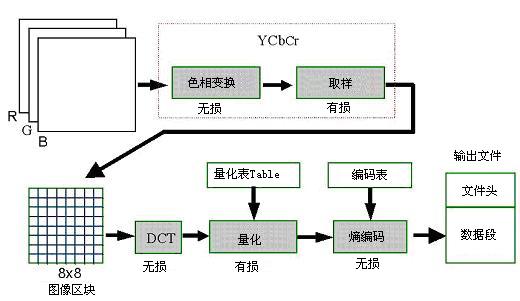
- 色彩空间转换
  $\quad$ 将 RGB 色彩空间转换到其他色彩空间，比如 YUV 色彩空间，根据人对亮度更敏感些，增加亮度的信号，减少颜色的信号，以这样“欺骗”人的眼睛的手段来节省空间。YUV 的格式也很多，常见的有 420 和 422 格式。在 420 格式中，每四个 Y 共用一组 UV 分量，每个 YUV 分量和 RGB 一样都用 8 位来表示，YUV 色彩空间就比 RGB 色彩空间所需的存储空间少一半，数据就被压缩到了一半。
- 将图像 8×8 分块
  $\quad$ 对图像按一定的采样格式进行采样，常见的格式有 4:4:4、4:2:2 和 4:2:0，采样完成后，将图像按 8×8(pixel) 划分成 MCU。
- 离散余弦变换 DCT
  - DCT 将时间或空间数据变成频率数据，利用人的听觉或视觉对高频信号（的变化）不敏感和对不同频带数据的感知特征不一样等特点，可以对多媒体数据进行压缩。
  - DCT 是数码率压缩需要常用的一个变换编码方法：①任何连续的实对称函数的傅里叶变换中只含余弦项，因此余弦变换与傅里叶变换一样有明确的物理意义；②由于大多数图像的高频分量较小，相应于图像高频分量的系数经常为零，加上人眼对高频成分的失真不敏感，所以可用更粗的量化。
  - 传送变换系数的数码率要大大小于传送图像像素所用的数码率，到达接收端后通过反离散余弦变换回到样值，虽然会有一定的失真，但人眼是可以接受的。
  - 二维正反离散余弦变换（FDCT/IDCT）的公式如下：
    $$C(\omega) = \begin{cases} \frac{1}{\sqrt{2}}, \space\space \omega = 0 \cr 1, \quad \omega \gt 0 \end{cases}$$ $$ FDCT: F(u, v) = \frac{2}{N} C(u)C(v) \sum_{x=0}^{N-1} \sum_{y=0}^{N-1} f(x, y) cos[\frac{(2x+1)u \pi}{2N}] cos[\frac{(2y+1)v \pi}{2N}]$$ $$IDCT: f(x, y) = \frac{2}{N} \sum_{u=0}^{N-1} \sum_{v=0}^{N-1} C(u)C(v)F(u, v) cos[\frac{(2x+1)u \pi}{2N}] cos[\frac{(2y+1)v \pi}{2N}]$$
    - 其中 $N$ 是像块的水平、垂直像素数，一般取 $N=8$。$N$ 大于 8 时效率增加不多但复杂性大为增加。8×8 的二维数据块经 DCT 后变成 8×8 个变换系数，这些系数都有明确的意义：$F(u=0, v=0)$ 是原 64 个样值的平均，相当于直流分量；随着 $u$、$v$ 值增加，相应系数分别代表逐步增加的水平空间频率和垂直空间频率分量的大小，如下图：
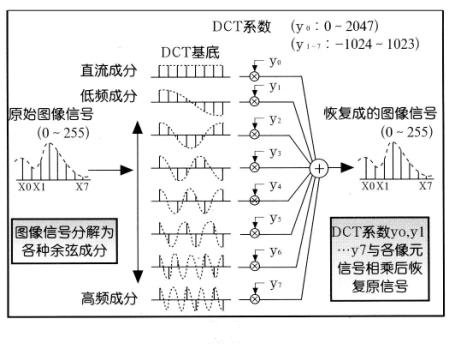
    - 图像信号被分解成直流信号+从低频到高频的各种余弦成分；DCT 系数只是表示了该种成分所占原图像信号的份额大小；显然，恢复图像信息可以表示这样一个矩阵形式：$f(x, y) = F(u, v) * C(u, v)$，$C(u, v)$ 是一个基底，$F(u, v)$ 是 DCT 系数，$f(x, y)$ 则是图像信号。

FDCT

inline double C(int w){
  return w>0?1:double(1/sqrt(2));
}
 
double func_F(int f[][8], int u, int v){
  double sum = 0;
  for(int i=0; i<8; i++){
    for(int j=0; j<8; j++){
      sum += f[i][j]*cos((2*i+1)*u*M_PI/16)*cos((2*j+1)*v*M_PI/16);
    }
  }
  return 0.25*C(u)*C(v)*sum;
}
 
// DCT transform 
void fdct(void){
  for(int row=0; row<8; row++){
    for(int col=0; col<8;col++){
      F[row][col] = func_F(f, row, col);
    }
  }
}

量化（quantization）
- 量化是对经过 FDCT 变换后的频率系数进行量化，是一个将信号的幅度离散化的过程，离散信号经过量化后变为数字信号；量化的目的是减少非“0”系数的幅度以及增加“0”值系数的数目，利用人眼对高频部分不敏感的特性来舍去高频部分。
- 对于有损压缩算法，JPEG 算法使用均匀量化器进行量化，量化步距是按照系数所在的位置和每种颜色分量的色调值来确定的，因为人眼对亮度信号比对色差信号敏感，因此使用了如下两种量化表：标准亮度量化表（bright_table.txt）和标准色差量化表（color_diff_table.txt）。

bright_table.txt

17	18	24	47	99	99	99	99
18	21	26	66	99	99	99	99
24	26	56	99	99	99	99	99
47	66	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99
99	99	99	99	99	99	99	99

color_diff_table.txt

16	11	10	16	24	40	51	61
12	12	14	19	26	58	60	55
14	13	16	24	40	57	69	56
14	17	22	29	51	87	80	62
18	22	37	56	68	109	103	77
24	35	55	64	81	104	113	92
49	64	78	87	103	121	120	101
72	92	95	98	112	100	103	99

由于人眼对低频分量的图像比对高频分量更敏感，因此左上角的量化步距要比右下角的量化步距小；把 DCT 系数块的数值除以对应量化表位置上的数值，并四舍五入到最近的整数；解码的时候，反量化步骤会乘回量化表相应值，但是四舍五入导致低频有所损失，高频“0”字段被舍弃；这一步为有损运算，会导致图像质量变低，量化是图像质量下降的最主要原因，所以说 JPEG 编码是有损压缩。

int Q[8][8];
int Sq[8][8];
 
void color_diff_quantization_table_init(const char* filename){
  ifstream in(filename);
  for(int row=0; row<8; row++){
    for(int col=0; col<8; col++){
      in >> Q[row][col];
    }
  }
  in.close();
}
 
// Sq(u,v) = round(F(u,v) / Q(u,v))
void quantilize(void){
  //color_diff_quantization_table_init("bright_table.txt");
  color_diff_quantization_table_init("color_diff_table.txt");
  
  for(int row=0; row<8; row++){
    for(int col=0; col<8;col++){
      Sq[row][col] = round(F[row][col] / Q[row][col]);
    }
  }
}

zig-zag Z 字形游程编码
$\quad$ 量化后的数据还可以通过以下 ZigZag 表的规则进行重排后，重排后的结果中可以看到出现连续的多个 0，达到简化、更大程度的去压缩，这样有利于进行游程编码。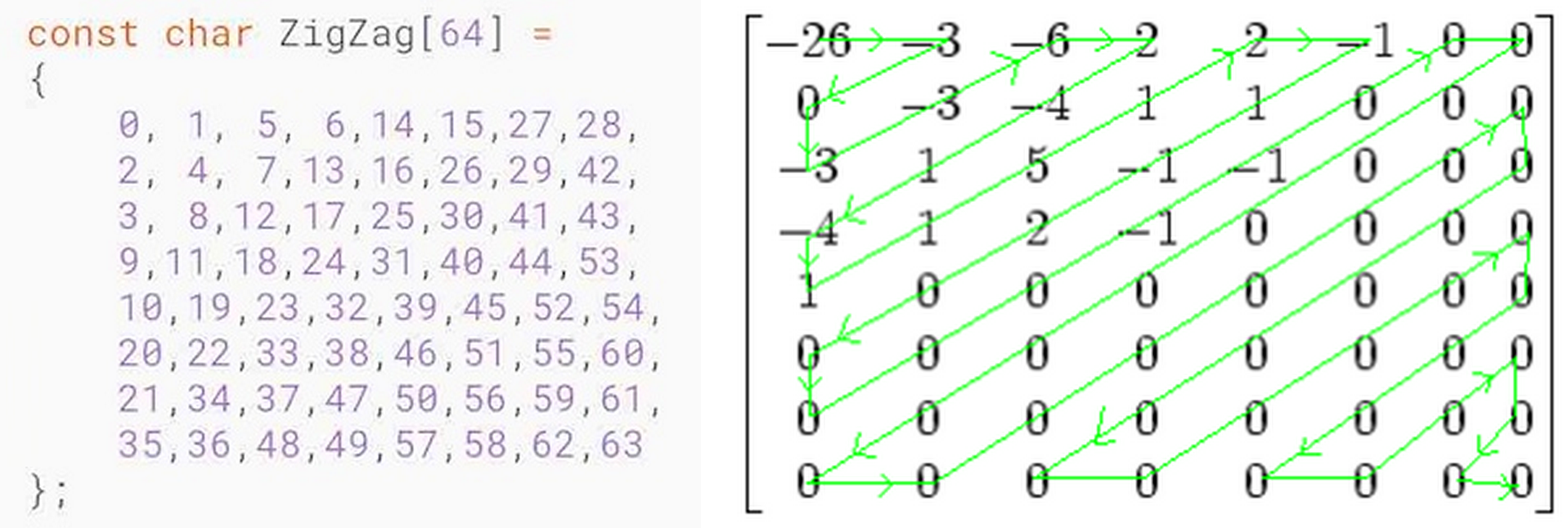
使用差分脉冲编码调制（DPCM）对直流系数（DC）进行编码
$\quad$ 8×8 图像经过 DCT 变换之后得到的 DC 直流系数有两个特点：一是系数的数值比较大；二是相邻 8×8 图像块的 DC 系数值变化不大。根据这两个特点，JPEG 算法使用了差分脉冲调制编码（DPCM）技术，对相邻图像块之间量化的 DC 系数的差值（Delta）进行编码：$Delta = DC(0, 0)_k - DC(0, 0)_{k-1}$
使用行程长度编码（RLE）对交流系数（AC）进行编码
- Z 字形读出的量化后的 AC 系数的特点是 1×64 矢量中包含有许多“0”系数并且许多“0”是连续的，因此使用非常简单和直观的游程长度编码（RLE）对它们进行编码：只将“0”作为重复的内容，JPEG 使用了一个字节的高4位来表示连续“0”的个数（最多重复内容可以记录数量为 15，超过 15 次要进行分段处理），而使用它的低4位来表示编码下一个非“0”系数所需要的位数；特别到最后，如果都是“0”，在读到最后一个数后，只要给出“快结束”（EOB）码字，就可以结束输出，因此节省了很多码率。
- 如下面的 4×4 图像块 $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 2 & 4 & 0 & 0 \\ 5 & 0 & 0 & 0 \\ 8 & 0 & 0 & 0 \end{bmatrix}$，按 Z 字形抽取得到的码字是：$\verb|{| 1, 0, 2, 5, 4, 0, 0, 0, 0, 8, 0, …, 0 \verb|}|$，经过游程编码得到的码值为：(0,1,0)(1,2,0)(0,5,0)(0,4,0)(4,8,1)EOB
熵编码（Huffman或算术）
- 使用熵编码还可以对 DPCM 编码后的直流 DC 系数和 RLE 编码后的交流 AC 系数作进一步的压缩；常用的熵编码有变长编码，即哈弗曼（Huffman）编码。
- Huffman 编码的基本原理：根据数据中元素出现的基本频率，调整元素的编码长度，以得到更高的压缩比；编码方法：对出现概率大的符号分配短字长的二进制码，对出现概率小的符号分配长字长的二进制码，得到符号的平均码长最短的码。
- Huffman 编码的步骤：
  1. 将符号按概率从小到大顺序从左至右排列叶节点；
  2. 连接两个概率最小的顶层节点来组成一个父节点，并在到左右子节点的两条连线上分别标记“0”和“1”（可以对概率大的赋值“0”，小的赋值“1”）；
  3. 重复步骤2，直到得到根节点，形成一棵二叉树；
  4. 从根节点开始到相应于每个符号的叶节点的 0/1 串，就是该符号的二进制编码。

#include <iostream>
#include <queue>
#include <map>
#include <climits> // for CHAR_BIT
#include <iterator>
#include <algorithm>
 
const int UniqueSymbols = 1 << CHAR_BIT;
const char* SampleString = "this is an example for huffman encoding";
 
typedef std::vector<bool> HuffCode;
typedef std::map<char, HuffCode> HuffCodeMap;
 
class INode {
public:
    const int f;
    virtual ~INode() {}
protected:
    INode(int f) : f(f) {}
};
 
class InternalNode : public INode {
public:
    INode *const left;
    INode *const right;
    InternalNode(INode* c0, INode* c1) : INode(c0->f + c1->f), left(c0), right(c1) {}
    ~InternalNode(){
        delete left;
        delete right;
    }
};
 
class LeafNode : public INode {
public:
    const char c;
    LeafNode(int f, char c) : INode(f), c(c) {}
};
 
struct NodeCmp{
    bool operator() (const INode* lhs, const INode* rhs) const { return lhs->f > rhs->f; }
};
 
INode* BuildTree(const int (&frequencies)[UniqueSymbols]) {
    std::priority_queue<INode*, std::vector<INode*>, NodeCmp> trees;
 
    for (int i = 0; i < UniqueSymbols; ++i) {
        if(frequencies[i] != 0)
            trees.push(new LeafNode(frequencies[i], (char)i));
    }
    while (trees.size() > 1) {
        INode* childR = trees.top();
        trees.pop();
 
        INode* childL = trees.top();
        trees.pop();
 
        INode* parent = new InternalNode(childR, childL);
        trees.push(parent);
    }
    return trees.top();
}
 
void GenerateCodes(const INode* node, const HuffCode& prefix, HuffCodeMap& outCodes) {
    if (const LeafNode* lf = dynamic_cast<const LeafNode*>(node)) {
        outCodes[lf->c] = prefix;
    }
    else if (const InternalNode* in = dynamic_cast<const InternalNode*>(node)) {
        HuffCode leftPrefix = prefix;
        leftPrefix.push_back(false);
        GenerateCodes(in->left, leftPrefix, outCodes);
 
        HuffCode rightPrefix = prefix;
        rightPrefix.push_back(true);
        GenerateCodes(in->right, rightPrefix, outCodes);
    }
}
 
int main() {
    // Build frequency table
    int frequencies[UniqueSymbols] = {0};
    const char* ptr = SampleString;
    while (*ptr != '\0')
        ++frequencies[*ptr++];
 
    INode* root = BuildTree(frequencies);
 
    HuffCodeMap codes;
    GenerateCodes(root, HuffCode(), codes);
    delete root;
 
    for (HuffCodeMap::const_iterator it = codes.begin(); it != codes.end(); ++it) {
        std::cout << it->first << " ";
        std::copy(it->second.begin(), it->second.end(),
                  std::ostream_iterator<bool>(std::cout));
        std::cout << std::endl;
    }
    return 0;
}

组成位数据流
$\quad$ JPEG 编码的最后一个步骤是把各种标记代码和编码后的图像数据组成一帧一帧的数据，这样做的目的是为了便于传输、存储和译码器进行译码，这样组织的数据通常称为 JPEG 位数据流（JPEG bitstream）。

JPEG 解码过程
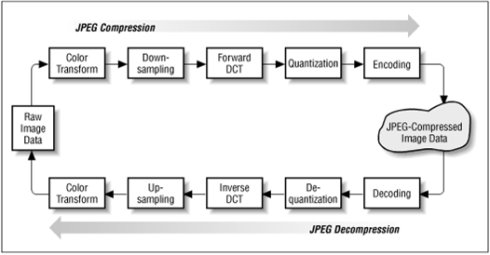
- AC 系数、DC 系数的解码
  $\quad$ 每个颜色分量单元都应该由两部分组成：1 个直流分量和 63 个交流分量。
- 直流系数的差分编码
- 反量化

// inverse quantization
int invSq[8][8];
 
// invSq(u,v) = Sq(u,v) * Q(u,v)
void inverse_quantilize(void){
  for(int row=0; row<8; row++){
    for(int col=0; col<8;col++){
      invSq[row][col] = Sq[row][col] * Q[row][col];
    }
  }
}

反 Zig-Zag 编码
反离散余弦变换（Inverse DCT）

// reconstructed sample data
int invV[8][8];
 
double func_f(int F[][8], int i, int j){
  double sum = 0;
  for(int u = 0; u<8; u++){
    for(int v=0; v<8; v++){
      sum += C(u)*C(v)*F[u][v]*cos((2*i+1)*u*M_PI/16)*cos((2*j+1)*v*M_PI/16);
    }
  }	
 
  return 0.25*sum;
}
 
void reconstruct(void){
  // inverse DCT transform
  for(int row=0; row<8; row++){
    for(int col=0; col<8;col++){
      invV[row][col] = func_f(invSq, row, col);
      // inverse of pre process
      invV[row][col] += 128;
    }
  }
}

YCrCb（YUV）向 RGB 转换

算术编码

算术编码克服了 Huffman 编码必须为整数位，这与实数的概率值相差大的缺点，如在 Huffman 编码中，本来只需要 0.1 位就可以表示的符号，却必须用 1 位来表示，结果造成 10 倍的浪费。算术编码所采用的解决办法是，不用二进制代码来表示符号，而改用 $[0，1)$ 中的一个宽度等于其出现概率的实数区间来表示一个符号，符号表中的所有符号刚好布满整个 $[0，1)$ 区间（概率之和为 1，不重不漏），把输入符号串（数据流）映射成 $[0，1)$ 区间中的一个实数值。
编码方法
- 符号串编码方法：将串中使用的符号表按原编码（如字符的ASCII编码、数字的二进制编码）从小到大顺序排列成表，计算表中每种符号 $s_i$ 出现的概率 $p_i$，然后依次根据这些符号概率大小 $p_i$ 来确定其在 $[0, 1)$ 期间中对应的小区间范围 $[x_i, y_i)$
  $$ x_i = \sum_{j=0}^{i-1} p_j, y_i = x_i + p_i, i=1, …, m$$
- 对输入符号串进行编码
  - 设串中第 $j$ 个符号 $c_j$ 为符号表中的第 $i$ 个符号 $s_i$，则可根据 $s_i$ 在符号表中所对应区间的上下限 $x_i$ 和 $y_i$，来计算编码区间 $I_j = [l_j, r_j)$：$l_j = l_{j-1} + d_{j-1}·x_i$，$r_j = l_{j-1} + d_{j-1}·y_i$；
  - 其中，$d_j = r_j - l_j$ 为区间 $I_j$ 的宽度，$l_0 = 0，r_0 = 1，d_0 = 1$。显然，$l_j$↑而 $d_j$ 与 $r_j$↓。串的最后一个符号所对应区间的下限 $l_n$ 就是该符号串的算术编码值。

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <math.h>
#include <algorithm>
#include <vector>
 
#define STRLEN 100
 
using namespace std;
 
int main() {
  char str[STRLEN], source_str[STRLEN];
  int str_len;
  cout << "Please input a string..." << endl;
  cin.getline(str, STRLEN);

  str_len = strlen(str);
  strcpy(source_str, str);
  printf("*input string length: ");
  cout << str_len << endl;
 
  printf("*sorting string letters in dictionary order: ");
  sort(str, str+str_len);
  printf("\"%s\"\n", str);
 
  vector<char> word;				//存放字符串中的字符word[i]
  vector<double> freq;				//存放word[i]字符所对应的频率freq[i]
  vector<double> endpoint;			//每个字符word[i]对应频率区间的左右点[endpoint[2i], endpoint[2i+1]);
   
  // 计算每个字母的频率(by dictionary order)
  for (int i = 0; i < str_len;){
    int tmp_num = 0;
    char cur_word = str[i];
    for (int j = i; j < str_len; j++){
      if (str[j] == cur_word){
        tmp_num++;
      }
      else{
        break;
      }
    }
    word.push_back(cur_word);
    freq.push_back(double(tmp_num) / str_len);
    i += tmp_num;
  }
 
  //for (int i = 0; i < word.size(); i++){
  //	cout << word[i]<< " " << freq[i] << endl;
  //}
   
  // 计算每个字母的频率区间的左右端点
  double left_endpoint = 0;
  for (int i = 0; i < word.size(); i++){
    endpoint.push_back(left_endpoint);
    left_endpoint += freq[i];
    endpoint.push_back(left_endpoint);
  }
  printf("\n----------- Symbol Table -----------\n");
  for (int i = 0; i < word.size(); i++){
    printf("\'%c\' %8.6lf [%8.6lf, %8.6lf)\n", word[i], freq[i], endpoint[2*i], endpoint[2*i+1]);
  }
  
  // 编码
  printf("\n----------- Arithmetic Coding -----------\n");
  double left = 0., right = 1., delta = 1.;
  for (int i = 0; i < str_len; i++){
    int index = 0;
    for (int j = 0; j < word.size(); j++){
      if (source_str[i] == word[j]){
        index = j;
        break;
      }
    }
    left = left + delta*endpoint[2 * index];
    right = left + delta*endpoint[2 * index + 1];
    // delta = right - left = delta * (endpoint[2 * index + 1] - endpoint[2 * index]) = delta * freq[index]
    delta = delta*freq[index];
    printf("%c %0.18lf %0.18lf %0.18lf\n", source_str[i], left, right, delta);
  }
  printf("*Arithmetic Coding Result: %.18lf\n", left);
  
  //...
  return 0;
}

解码方法
- 由符号表（包括符号对应的概率与区间）和实数编码 $l_n$，可以按下面的解码算法来重构输入符号串。
  - ① 设 $v_1 = l_n = \space$码值；
  - ② 若 $v_j \in [x_i, y_j) \Longrightarrow c_j = s_i, j = 1, …, n$；
  - ③ $v_{j+1} = \frac{v_j - x_i}{p_j}, j = 1, …, n-1$，重复步骤②、③。

vector<char> word;				//存放字符串中的字符word[i]
vector<double> freq;				//存放word[i]字符所对应的频率freq[i]
vector<double> endpoint;			//每个字符word[i]对应频率区间的左右点[endpoint[2i], endpoint[2i+1]);
 
printf("*Arithmetic Coding Result: %.18lf\n", left);
 
printf("\n----------- Arithmetic Decoding -----------\n");
double v = left;
for (int i = 0; i < str_len; i++){
  int index = 0;
  for (int j = 0; j < word.size(); j++){
    if (v < endpoint[2 * j + 1]){
      index = j;
      break;
    }
  }
  printf("%.18lf %d \'%c\'\n", v, index+1, word[index]);
  v = (v - endpoint[2 * index]) / freq[index];
}

LZW编码

LZW 编码和 Huffman编码、算术编码一样，是无损压缩中的一种；该算法通过建立字典，实现字符重用与编码，适用于 source 中重复率很高的文本压缩。
- LZW 算法是一种基于字典的编码——将变长的输入符号串映射成定长的码字——形成一本短语词典索引（串表），利用字符出现的频率冗余度及串模式高使用率冗余度达到压缩的目的。该算法只需一遍扫描，且具有自适应的特点（从空表开始逐步生成串表，码字长从 1 逐步增加到12），不需保存和传送串表。
- 串表具有前缀性——若串 $wc$（$c$ 为字符）在串表中，则串 $w$ 也在串表中（所以，可初始化串表为含所有单个字符的串）。
- 匹配采用贪婪算法——每次只识别与匹配串表中最长的已有串 $w$（输出对应的码字）、并可与下一输入字符 $c$ 拼成一个新的码字 $wc$。
LZW 压缩算法
- 初始化
  - ①将所有单个字符（$n$ 个不同字符）的串放入串表 ST 中（共 $n$ 项[码字为$1~n$]，实际操作时不必放入，只需空出串表的前 $n$ 项，字符对应码字所对应的串表索引即可）；
  - ②读首字符入前缀串 $w$；
  - ③设置码长 $codeBits = n+1$；
  - ④设置串表中当前表项的索引值 $next = 初始码字 = n+1$
- 循环
  - ⑤读下一输入字符 $c$；
  - ⑥若 $c=EOF$（文件结束符），则输出 $w$ 的码字 $dict[w]$，结束循环（输出结束码字）；
  - ⑦若 $wc$ 已在串表中，则 $w = wc$，转到循环开始处⑤；否则，输出 $w$ 的码字 $dict[w]$，将 $wc$ 放入 ST 中的 $next$ 处，$next++$；令 $w=c$，转到循环开始处⑤；
  - ⑧若 $next$ 的位数超过码长（$\gt codeBits$），则 $codeBits++$；若串表已满（$next$ 的位数已超过最大码长 12），则清空串表，输出清表码字，转到初始化开始处①（一般不太可能发生）。

#! /usr/bin/env python
# coding= utf-8
 
import sys
 
reload(sys)
sys.setdefaultencoding('utf-8')
 
input = raw_input(u"请输入字符串：".encode('mbcs'))
print u"编码过程："
inputlist = list(input)
 
wclist = list(set(inputlist))
diclen = len(wclist)
wclist.sort()
phrases_dict = {}
 
for x in xrange(1, diclen+1):
    phrases_dict[x] = wclist[x-1]
 
nextlist = range(1, len(wclist)+1)
wlist = ['--'] * len(wclist)
procedurelist = ['--'] * len(wclist)
poslist = ['--']*len(wclist)
mstr = ''
nstr = ''
k = 0
 
for i in range(0, len(inputlist)):
    nstr = nstr + inputlist[i]
    if nstr in wclist:
        mstr = nstr
    else:
        k = k+1
        wclist.append(nstr)
        nextlist.append(len(nextlist)+1)
        a = wclist.index(mstr)
        wlist.append(a+1)
        procedurelist.append(k)
        poslist.append(i-len(nstr)+2)
        mstr = inputlist[i]
        nstr = inputlist[i]
 
wclist.append('--')
nextlist.append('--')
a = wclist.index(mstr)
wlist.append(a+1)
procedurelist.append(k+1)
poslist.append('--')
 
print u'步 骤  位 置   Next      Wc      输出W'
for i in xrange(0, len(wclist)):
    print '%s\t %s\t %s\t %s\t %s\t'%(procedurelist[i], poslist[i], nextlist[i], wclist[i], wlist[i])

LZW 还原算法
- 初始化
  - ①将所有单个字符（$n$ 个不同字符）的串放入串表 ST 中（共 $n$ 项[码字为$1~n$]，实际操作时不必放入，只需空出串表的前 $n$ 项，字符对应码字所对应的串表索引即可）；
  - ②设置码长 $codeBits = n+1$；
  - ③设置串表中当前表项的索引值 $next = 初始码字 = n+1$
  - ④读首个码字（所对应的单个字符）入老串 $old$，输出该字符；
- 循环
  - ⑤读下一码字 $new$：若 $new$ 为结束码字，结束循环；若 $new$ 为清表码字，清空串表，转到初始化开始处①；
  - ⑥若 $new \geq next$，则输出串 $newStr = old + old[0]$（例外处理）；若 $new \lt next$，则输出串 $newStr = ST[new]$；
  - ⑦将 $old + newStr[0]$ 放入串表 ST[next] 中，$next++$；
  - ⑧若 $next$ 的位数超过码长（$\gt codeBits$），则 $codeBits++$；若加一后 $codeBits \gt 12$，则重新让 $codeBits = 12$；
  - ⑨$old = newStr$，转到循环开始处⑤。

def print_before_decode(phrases_dict):
    print u'步骤 码字   词 典    输 出'
    keys = sorted(list(phrases_dict.keys()))
    for key in keys:
        print '%-4s %-4s %-4s %-5s %-4s' % \
            ('', '', '(' + str(key) + ')', phrases_dict[key], '')
 
def decodeLZW(codes, phrases_dict):
    step = 1
    next = len(phrases_dict) + 1
    old = phrases_dict[codes[0]]
    print '%-4s %-4s %-4s %-5s %-4s' % \
        (step, '(1)', '-', '-', old)
    for i in range(1, len(codes)):
        new = codes[i]
        if new >= next:
            newStr = old + old[0]
        else:
            newStr = phrases_dict[new]
        phrases_dict[next] = old + newStr[0]
        step += 1

        print '%-4s %-4s %-4s %-5s %-4s' % \
            (step, '(' + str(new) + ')', '(' + str(next) + ')',
             phrases_dict[next], newStr)
        next += 1
        old = newStr
 
print u"解码过程："
codes = wlist[diclen:]
print_before_decode(phrases_dict)
decodeLZW(codes, phrases_dict)

References

本文标题:JPEG编码&算术编码、LZW编码

文章作者:Gary

发布时间:2017-07-11, 18:02:16

最后更新:2020-03-28, 12:37:22

原始链接:http://durant35.github.io/2017/07/11/programPearls_JPEG$Arithmetic$LZW/